超聲速下柵格舵展開過程數(shù)值模擬*

周培培,郭少杰,王　斌

(中國航天空氣動(dòng)力技術(shù)研究院,北京　100074)

?

超聲速下柵格舵展開過程數(shù)值模擬*

周培培,郭少杰,王斌

(中國航天空氣動(dòng)力技術(shù)研究院,北京100074)

摘要:柵格舵從折疊到展開的過程中氣動(dòng)特性變化劇烈,對展開可靠性和導(dǎo)彈整體氣動(dòng)特性的影響都比較大。針對柵格舵這種復(fù)雜的構(gòu)造形式,生成了帶有棱柱層的非結(jié)構(gòu)網(wǎng)格,再結(jié)合重疊網(wǎng)格技術(shù)對柵格舵導(dǎo)彈超聲速繞流流場進(jìn)行了數(shù)值模擬,計(jì)算結(jié)果與風(fēng)洞試驗(yàn)結(jié)果吻合較好。在此基礎(chǔ)上,對超聲速下柵格舵動(dòng)態(tài)展開過程的非定常流場進(jìn)行了數(shù)值模擬,分析了柵格舵導(dǎo)彈動(dòng)態(tài)氣動(dòng)特性的變化規(guī)律。

關(guān)鍵詞:柵格舵;非結(jié)構(gòu)重疊網(wǎng)格;數(shù)值模擬;展開過程

0引言

柵格舵是一種非常規(guī)的氣動(dòng)控制舵面,最早由前蘇聯(lián)研究人員于20世紀(jì)40年代提出,俄羅斯在20世紀(jì)90年代首次成功應(yīng)用于R-77蝰蛇空空導(dǎo)彈上。由于柵格舵的升力特性好、鉸鏈力矩小、易于折疊、打開等諸多優(yōu)點(diǎn),所以在導(dǎo)彈上的安裝多處于折疊狀態(tài)。柵格舵展開過程中的導(dǎo)彈氣動(dòng)特性的明顯變化對柵格舵展開可靠性非常重要,為此需要研究柵格舵展開過程中氣動(dòng)特性的變化規(guī)律。

國內(nèi)外學(xué)者對柵格舵這種氣動(dòng)外形開展了大量的研究分析[1-12]。以前的研究工作主要是理論分析和風(fēng)洞試驗(yàn),隨著計(jì)算機(jī)硬件資源的飛速發(fā)展和計(jì)算方法的進(jìn)步,數(shù)值模擬(CFD)成為一種重要的研究手段。但柵格舵是由許多薄格壁組成的柵格狀或者蜂窩狀結(jié)構(gòu),對這種復(fù)雜外形生成質(zhì)量高、數(shù)量少的計(jì)算網(wǎng)格是比較困難的。從研究文獻(xiàn)上看,對柵格舵繞流流場數(shù)值模擬采用的網(wǎng)格主要有直角網(wǎng)格[11]、非結(jié)構(gòu)網(wǎng)格、結(jié)構(gòu)/非結(jié)構(gòu)混合網(wǎng)格[8-9]、分區(qū)結(jié)構(gòu)網(wǎng)格[7]、結(jié)構(gòu)重疊網(wǎng)格[12]等。這些網(wǎng)格策略各有優(yōu)缺點(diǎn):直角網(wǎng)格、非結(jié)構(gòu)網(wǎng)格適應(yīng)復(fù)雜外形能力強(qiáng),網(wǎng)格生成時(shí)間短,但不能很好的解決附面層黏性問題;而結(jié)構(gòu)網(wǎng)格對復(fù)雜外形適應(yīng)能力差,針對柵格舵這種外形網(wǎng)格生成難度非常大,耗時(shí)耗力。

文中針對非結(jié)構(gòu)網(wǎng)格的缺點(diǎn),采取在物體表面外推生成棱柱層的方法,提高其對附面層黏性效應(yīng)的模擬精度。通過對彈體和柵格舵單獨(dú)生成帶有棱柱層的非結(jié)構(gòu)網(wǎng)格,并采用重疊網(wǎng)格的方法確定兩個(gè)網(wǎng)格域的重疊關(guān)系,利用網(wǎng)格域間的相對運(yùn)動(dòng)實(shí)現(xiàn)柵格舵從折疊到展開的動(dòng)態(tài)過程。通過柵格舵展開狀態(tài)超聲速定常流場的數(shù)值模擬對計(jì)算方法和網(wǎng)格策略的可靠性進(jìn)行了數(shù)值驗(yàn)證。在此基礎(chǔ)上,對超聲速下柵格舵展開過程非定常繞流流場進(jìn)行了數(shù)值模擬,分析了柵格舵展開過程中氣動(dòng)特性的變化規(guī)律。

1數(shù)值模擬方法

1.1控制方程

計(jì)算采用的控制方程為非定常雷諾時(shí)均N-S方程,一般曲線坐標(biāo)系下的N-S方程可寫作:

(1)

式中:Q表示守恒變量矢量'F、G和H表示無黏矢通量;Fv、Gv和Hv表示黏性矢通量。N-S方程組采用守恒形式的有限體積法離散,采用雙時(shí)間步方法結(jié)合隱式格式時(shí)間推進(jìn)求解,使用的湍流模型為兩方程的k-ε渦粘性湍流模型。

1.2邊界條件

超音速遠(yuǎn)場入流邊界所有參數(shù)為自由來流值,出流邊界所有參數(shù)由內(nèi)流場外插得到;柵格舵導(dǎo)彈對稱面按對稱條件處理;物面采用無滑移絕熱邊界條件;重疊邊界上的信息傳遞由流場插值得到。

2網(wǎng)格生成

2.1數(shù)值計(jì)算模型

數(shù)值計(jì)算模型為包含彈體、彈翼和柵格舵的“XX”布局柵格舵導(dǎo)彈,外形如圖1所示。

圖1　柵格舵導(dǎo)彈外形圖

2.2帶棱柱層的非結(jié)構(gòu)網(wǎng)格

傳統(tǒng)的非結(jié)構(gòu)空間網(wǎng)格為四面體單元,物面附近附面層內(nèi)網(wǎng)格較稀疏,難以有效模擬附面層內(nèi)的黏性流動(dòng)。文中在柵格舵導(dǎo)彈表面三角形網(wǎng)格單元基礎(chǔ)上通過外推生成五面體的棱柱形網(wǎng)格單元,既可以保證物面附近網(wǎng)格的正交性,又可以有效的控制附面層內(nèi)的網(wǎng)格密度,而不至于增加太多的網(wǎng)格數(shù)量。圖2給出了彈翼和柵格舵表面局部非結(jié)構(gòu)網(wǎng)格,圖3給出了彈體頭部和柵格舵剖面外推棱柱層空間網(wǎng)格。

在超聲速下,柵格框內(nèi)會產(chǎn)生復(fù)雜的激波與邊界層干涉,流場特性復(fù)雜,為了能較為精細(xì)的捕捉到流場特征,對柵格舵附近的網(wǎng)格進(jìn)行了局部加密,保證在流動(dòng)變化劇烈的區(qū)域有一定的網(wǎng)格密度。

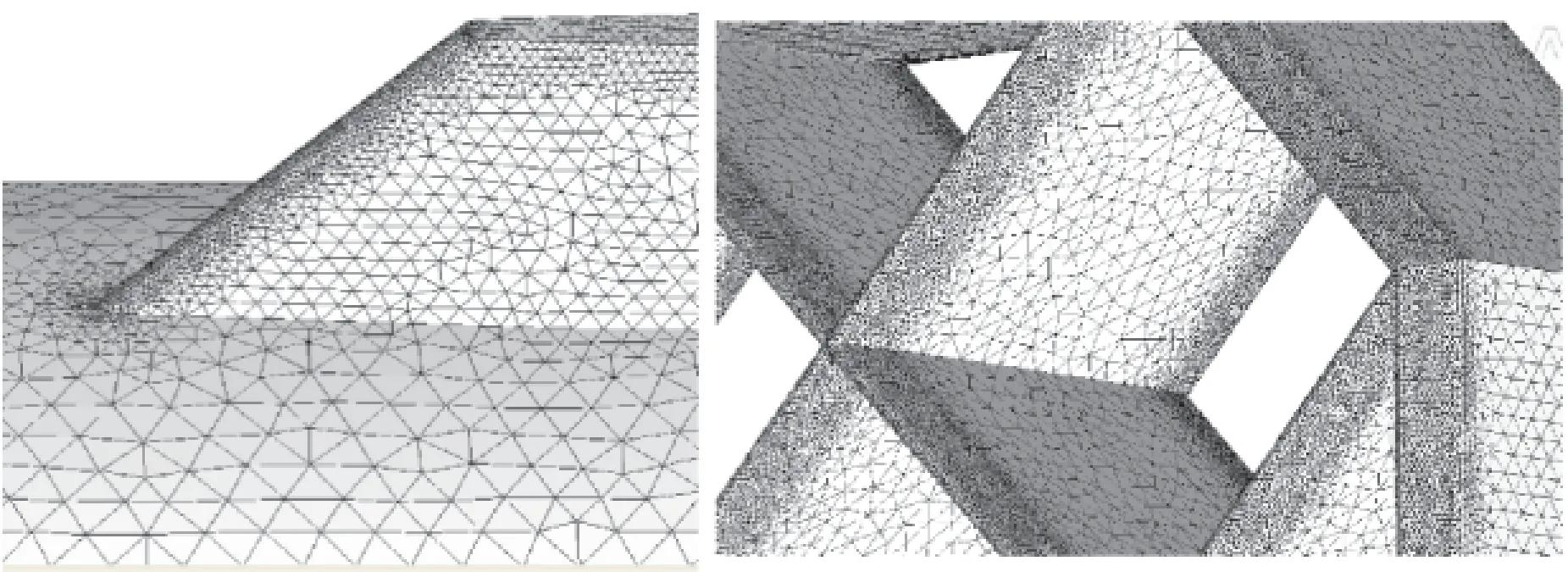
圖2　彈翼和柵格舵局部表面網(wǎng)格示意圖

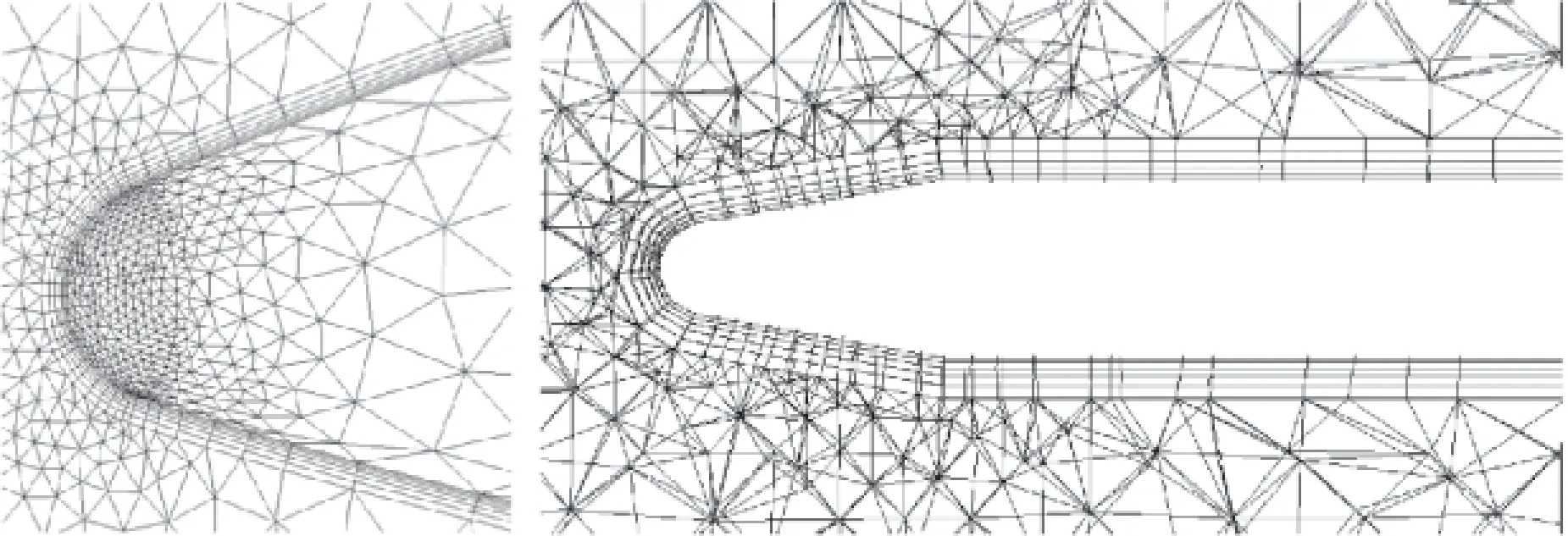
圖3　彈體頭部及舵剖面空間網(wǎng)格示意圖

2.3重疊網(wǎng)格

針對柵格舵和彈體單獨(dú)生成帶棱柱層的非結(jié)構(gòu)網(wǎng)格。在此基礎(chǔ)上,通過重疊網(wǎng)格技術(shù)實(shí)現(xiàn)柵格舵網(wǎng)格域和彈體網(wǎng)格域的重疊關(guān)系,在柵格舵網(wǎng)格域外邊界上進(jìn)行挖洞處理,隱藏位于其內(nèi)的彈體域網(wǎng)格,只在重疊邊界上進(jìn)行流場信息的插值交換。通過網(wǎng)格域間的相對運(yùn)動(dòng)即可描述物體間的任意運(yùn)動(dòng),而且整個(gè)運(yùn)動(dòng)過程中只需要搜索重疊邊界,然后進(jìn)行網(wǎng)格域間的挖洞處理,而不需要網(wǎng)格重新生成,因此具有很高的效率和穩(wěn)定性。圖4給出了柵格舵折疊狀態(tài)下空間剖面的重疊網(wǎng)格圖,圖5給出了柵格舵展開狀態(tài)下空間剖面的重疊網(wǎng)格圖。

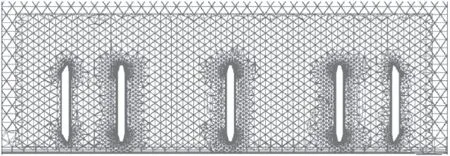
圖4　柵格舵折疊狀態(tài)下空間剖面的重疊網(wǎng)格

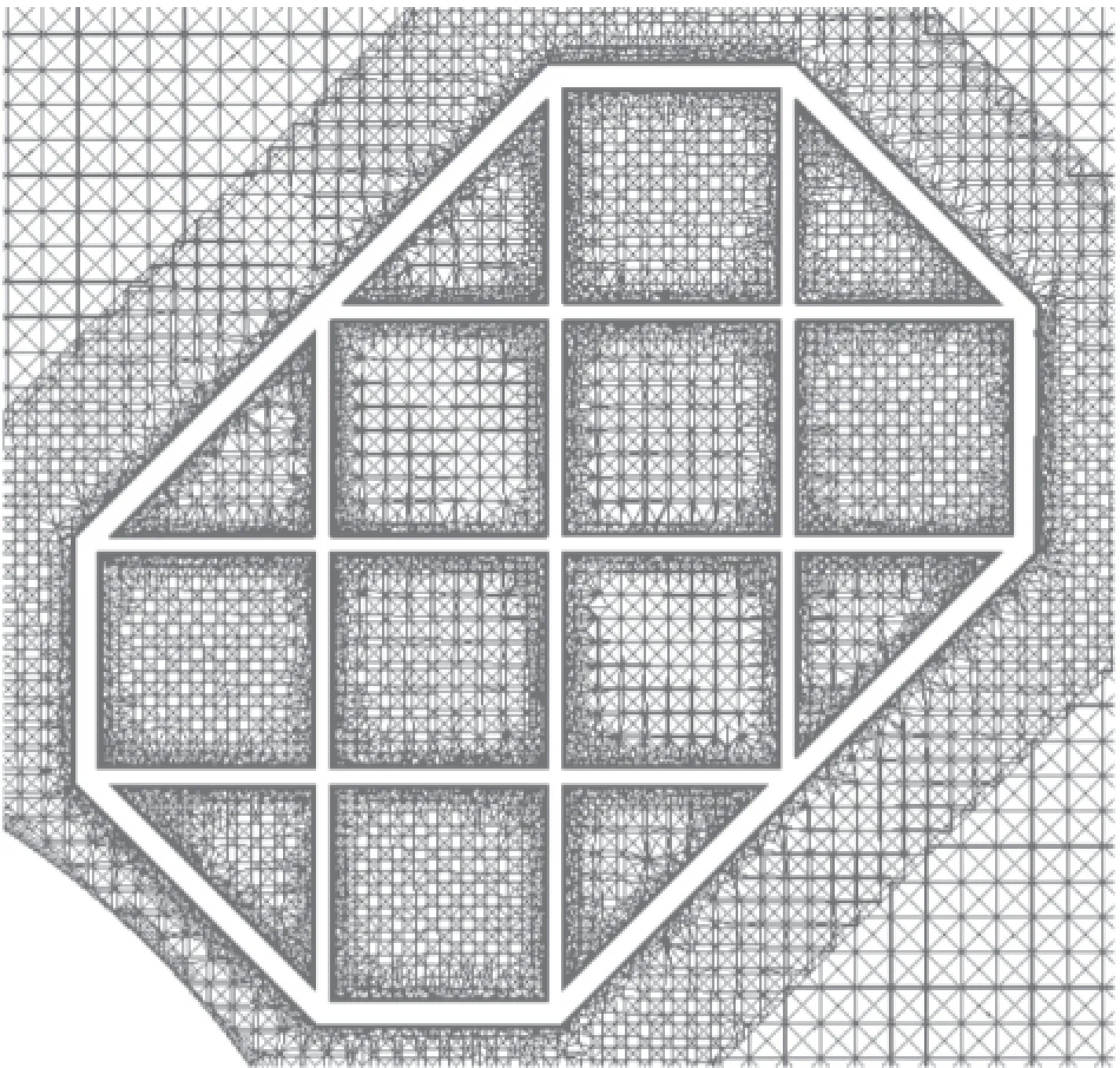
圖5　柵格舵展開狀態(tài)下空間剖面的重疊網(wǎng)格

3數(shù)值方法的計(jì)算驗(yàn)證

首先針對柵格舵展開狀態(tài),開展了超聲速下(Ma=3,α=-4°～30°)非結(jié)構(gòu)重疊網(wǎng)格和數(shù)值方法的計(jì)算驗(yàn)證工作,并將不同攻角下數(shù)值計(jì)算結(jié)果與實(shí)驗(yàn)數(shù)據(jù)進(jìn)行了對比分析。圖6給出了Ma=3條件下法向力、俯仰力矩系數(shù)計(jì)算結(jié)果與實(shí)驗(yàn)數(shù)據(jù)的比較,圖7給出了Ma=3條件下軸向力系數(shù)與實(shí)驗(yàn)的比較以及Ma=3,α=8°條件下柵格舵導(dǎo)彈表面壓力云圖。

從計(jì)算和試驗(yàn)結(jié)果的對比可以看出,以生成棱柱層的非結(jié)構(gòu)重疊網(wǎng)格為基礎(chǔ),求解N-S方程得到的計(jì)算結(jié)果與實(shí)驗(yàn)數(shù)據(jù)吻合良好,能夠準(zhǔn)確的捕捉柵格舵導(dǎo)彈的流場特性,驗(yàn)證了數(shù)值方法和采用的網(wǎng)格策略的合理性和可靠性。

圖6　Ma=3條件下法向力系數(shù)、俯仰力矩系數(shù)與實(shí)驗(yàn)的比較

圖7　Ma=3條件下軸向力系數(shù)與實(shí)驗(yàn)的比較以及α=8°時(shí)柵格舵導(dǎo)彈表面壓力云圖

4柵格舵展開過程的數(shù)值模擬

柵格舵的展開過程時(shí)間短,作用在柵格舵上的氣動(dòng)載荷變化大,造成柵格舵上的氣動(dòng)特性變化劇烈,對彈體有較大沖擊。為此進(jìn)行了超聲速下柵格舵折疊到展開過程非定常流場的數(shù)值模擬,得到了導(dǎo)彈上氣動(dòng)特性的變化規(guī)律。計(jì)算狀態(tài)為Ma=3,α=5°,設(shè)定展開過程需要10 ms,展開角速度設(shè)為157 rad/s。

圖8給出了背風(fēng)舵、迎風(fēng)舵及全彈的軸向力系數(shù)、法向力系數(shù)隨展開角度的變化曲線。可以看出舵面與導(dǎo)彈的軸向力變化規(guī)律相似,隨展開角度先增大后減小,大約在展開45°角時(shí)達(dá)到最大,呈倒“V”字形分布。全彈法向力隨展開角度增大而緩慢增大,在展開80°角后,略有減小;舵面上的法向力在展開40°角前緩慢增大(迎風(fēng)舵為正,背風(fēng)舵為負(fù)),之后變化劇烈,在展開60°左右達(dá)到最大,60°角后迅速減小。

圖9給出了舵面?zhèn)认蛄ο禂?shù)、全彈俯仰力矩系數(shù)和壓心隨展開角度的變化曲線,可以看出背風(fēng)舵和迎風(fēng)舵的側(cè)向力系數(shù)變化規(guī)律相似,大小接近,呈“V”字形分布,在展開55°左右達(dá)到最大。全彈俯仰力矩系數(shù)隨展開角度緩慢增大,展開80°角后略有減小;全彈壓心隨展開角度逐漸后移,展開80°角后略有前移,折疊展開壓心后移量為11%。

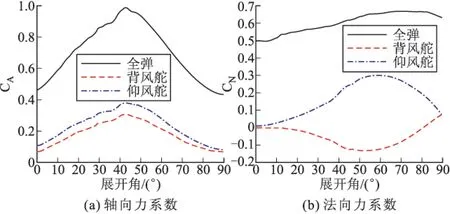
圖8　Ma=3,α=5°條件下軸向力系數(shù)、法向力系數(shù)隨展開角變化曲線

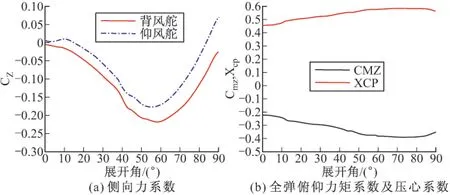
圖9　Ma=3,α=5°條件下側(cè)向力系數(shù)、全彈俯仰力矩系數(shù)及壓心系數(shù)隨展開角變化曲線

5主要結(jié)論

文中采用在物面外推生成棱柱層的方法,提高了非結(jié)構(gòu)網(wǎng)格的黏性模擬能力,并利用重疊網(wǎng)格技術(shù)對柵格舵展開過程的非定常流場進(jìn)行了數(shù)值模擬分析,得到以下結(jié)論:

1)文中采用的網(wǎng)格生成策略和數(shù)值計(jì)算方法可以可靠的模擬柵格舵導(dǎo)彈的氣動(dòng)特性。

2)在舵面展開過程中,全彈法向力和低頭力矩隨展開角度先緩慢增大,在80°角后略微減小,;軸向力系數(shù)先增大后減小,大約在展開45°角時(shí)達(dá)到最大;全彈壓心隨展開角度逐漸后移,80°角后略有前移,折疊到展開的壓心后移量為11%。

3)在舵面展開過程中,迎風(fēng)舵和背風(fēng)舵的法向力系數(shù)變化規(guī)律相反,軸向力系數(shù)和側(cè)向力系數(shù)變化規(guī)律相同。

參考文獻(xiàn):

[1]DESPIRITOJ,EDGEHL,WEINACHTP,etal.CFDAnalysisofgridfinsformaneuveringmissiles:AIAA2000-0391 [R]. 2000.

[2]DESPIRITOJ,SAHUJ.ViscousCFDcalculationsofgridfinmissileaerodynamicinthesupersonicflowregion:AIAA2001-0257 [R]. 2001.

[3]CHENS,KHALIDM,XUH.AcomprehensiveCFDinvestigationofgridfinsasefficientcontrolsurfacedevices:AIAA2000-0987 [R]. 2000.

[4]LINHerng,HUANGJuan-chen.Navier-stokescomputationforbody/cruciformgridfinconfiguration:AIAA2002-2722 [R]. 2002.

[5]RAVINDRAK,NIKHILVShende,BALAKRISHNANN.CFDsimulationofthegridfinflows:AIAA2013-3023 [R]. 2013.

[6]周培培. 基于結(jié)構(gòu)網(wǎng)格的柵格舵繞流數(shù)值模擬 [J]. 空氣動(dòng)力學(xué)學(xué)報(bào), 2014, 32(3): 334-338.

[7]周培培, 蔣勝矩, 李杰. 基于動(dòng)態(tài)嵌套網(wǎng)格的非定常氣動(dòng)力數(shù)值模擬 [J]. 彈箭與制導(dǎo)學(xué)報(bào), 2010, 30(5): 143-146.

[8]吳曉軍, 馬明生, 鄧有奇, 等. 結(jié)構(gòu)/非結(jié)構(gòu)混合網(wǎng)格數(shù)值模擬柵格舵 [J]. 空氣動(dòng)力學(xué)學(xué)報(bào), 2009, 27(4): 419-423.

[9]劉剛, 肖中云, 江雄, 等. 混合網(wǎng)格方法在柵格舵數(shù)值模擬中的應(yīng)用研究 [J]. 空氣動(dòng)力學(xué)學(xué)報(bào), 2007, 25(2): 277-280.

[10]鄧帆, 陳少松, 余勇剛. 亞跨音速柵格的升阻特性數(shù)值研究 [J]. 彈道學(xué)報(bào), 2009, 21(4): 34-37.

[11]王斌, 張衛(wèi)民. 柵格舵氣動(dòng)特性數(shù)值研究 [J]. 戰(zhàn)術(shù)導(dǎo)彈技術(shù), 2011(2): 31-33.

[12]王學(xué)占, 王立強(qiáng). 基于結(jié)構(gòu)重疊網(wǎng)格的柵格舵導(dǎo)彈流場數(shù)值仿真 [J]. 航空兵器, 2012(2): 44-47.

*收稿日期:2015-03-24

作者簡介:周培培(1984-),男,河南南陽人,工程師,碩士,研究方向:飛行器設(shè)計(jì)與計(jì)算空氣動(dòng)力學(xué)；通訊作者:郭少杰，工程師，E-mail:13720041809@qq.com。

中圖分類號:V211.3

文獻(xiàn)標(biāo)志碼:A

The Deployment Process Simulation of Grid Fin Under Supersonic Airflow

ZHOU Peipei,GUO Shaojie,WANG Bin

(China Academy of Aerospace Aerodynamics, Beijing 100074, china)

Abstract:Rapid variation of aerodynamic characteristics in deployment makes great impact on unfolding reliability and aerodynamic characteristics of grid fin missile. In this paper, a high quality unstructured grid with prismatic layers generated for such a complex geometry, and chimera grid was applied to combine computation domain around body and grid fins, then N-S equations were solved numerically to simulate supersonic flow field of grid fin missile. The simulation results show excellent agreement with the experiment data. Based on grid strategy and numerical method, the deployment process of grid fins was simulated under supersonic airflow, and dynamic aerodynamic characteristics were obtained.

Keywords:grid fins; unstructured chimera grid; numerical simulation; deployment process