振幅影響隧道混凝土累積損傷特征的試驗(yàn)研究

彭立敏，劉寧，施成華

(中南大學(xué) 土木工程學(xué)院， 湖南 長沙 410075)

?

振幅影響隧道混凝土累積損傷特征的試驗(yàn)研究

彭立敏，劉寧，施成華

(中南大學(xué) 土木工程學(xué)院， 湖南 長沙 410075)

摘要:重載列車軸重的增加導(dǎo)致振動幅值的提高，進(jìn)而引起隧底結(jié)構(gòu)損傷破壞的發(fā)生。針對仰拱混凝土累積損傷方面研究的不足且未引入隧道設(shè)計規(guī)范中，基于Helmholtz自由能理論體系，開展用于描述循環(huán)荷載引起仰拱混凝土累積損傷特征計算模型的研究。為了驗(yàn)證累積損傷模型并獲取滿足隧底力學(xué)環(huán)境的混凝土損傷計算方法，進(jìn)行靜載與循環(huán)荷載耦合環(huán)境中不同振動幅值作用下仰拱混凝土的試驗(yàn)研究。實(shí)驗(yàn)數(shù)據(jù)及數(shù)值計算結(jié)果表明：混凝土損傷演化曲線可以分為3個階段：初期增長階段、穩(wěn)定增長階段和快速發(fā)展階段。通過對不同階段混凝土損傷演化趨勢的非線性擬合分析，給出能夠引發(fā)混凝土損傷破壞的靜載水平和不同階段損傷演化趨勢的定量表達(dá)式。通過數(shù)值計算與試驗(yàn)結(jié)果對比分析，得到混凝土試件損傷主要分布在中間受拉區(qū)域，底部損傷值相對較大并最終發(fā)生破壞。初始階段損傷首先發(fā)生在混凝土試塊中底部，混凝土損傷由試件下部逐漸向上逐漸發(fā)展。

關(guān)鍵詞：累積損傷模型；仰拱混凝土；循環(huán)荷載；振動幅值

隨著全球經(jīng)濟(jì)的快速融合和地區(qū)間經(jīng)濟(jì)的發(fā)展，重載鐵路運(yùn)輸將成為鐵路發(fā)展的重要方向[1]，并通過增加貨運(yùn)列車軸重和長度以滿足貨運(yùn)需求。在大重量、高密度的運(yùn)營條件下，使軌下基礎(chǔ)承受更大的振動荷載，使得線路狀態(tài)和軌道結(jié)構(gòu)及底部結(jié)構(gòu)破壞特征較傳統(tǒng)線路變化明顯[2-3]。隧道底部結(jié)構(gòu)承受圍巖壓力和列車振動荷載的作用，然而軸重的提高直接引起動載幅值的增大，當(dāng)動載幅值并達(dá)到一定量值，進(jìn)而產(chǎn)生隧底結(jié)構(gòu)累積損傷。隧底結(jié)構(gòu)的受力狀態(tài)直接影響到整個隧道結(jié)構(gòu)的安全穩(wěn)定[4-5]。基于連續(xù)損傷力學(xué)，國內(nèi)外學(xué)者建立了多種考慮靜載及動載作用混凝土損傷模型[6],用于描述靜載及動載引起混凝土損傷的研究未考慮不同動載幅值影響，并且對于混凝土構(gòu)件損傷特征的一般僅給出經(jīng)驗(yàn)公式。在早期有學(xué)者，主要通過試驗(yàn)得到疲勞壽命曲線，并得到廣泛應(yīng)用。然而上述模型不能很好地表征靜載和動載耦合作用下隧底結(jié)構(gòu)混凝土的累積損傷規(guī)律。Hsu等進(jìn)行了循環(huán)荷載作用下混凝土單軸拉壓試驗(yàn)研究。提出了疲勞壽命曲線并加以改進(jìn)，并進(jìn)行了損傷量與物理量之間的關(guān)系的探討。然而，上述研究經(jīng)驗(yàn)?zāi)Ｐ筒荒軠?zhǔn)確的描述混凝土損傷壽命預(yù)測和損傷的整個過程。試驗(yàn)采用機(jī)電阻抗探測技術(shù)，通過結(jié)構(gòu)表面壓電陶瓷片的黏貼可以進(jìn)行損傷探測、強(qiáng)度預(yù)測、損傷評估及其健康檢測[7-8]。對于結(jié)構(gòu)健康檢測，通過陶瓷壓電片獲取的主要的損傷指標(biāo)，損傷的變化能夠較好的得到和量化。混凝土損傷監(jiān)測新的方法解決了動載作用全過程損傷探測與采集的問題[9]。本文首先建立用于描述混凝土累積損傷特征的計算模型，并進(jìn)行模擬隧底力學(xué)環(huán)境條件不同動載幅值作用混凝土試驗(yàn)。通過試驗(yàn)數(shù)據(jù)及數(shù)值計算驗(yàn)證累積損傷計算模型，并對仰拱混凝土累積損傷演化規(guī)律、分布特征及發(fā)展規(guī)律進(jìn)行分析，給出滿足隧底力學(xué)環(huán)境條件混凝土損傷計算方法。

1累積損傷模型

1.1損傷變量和有效變量的描述

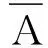
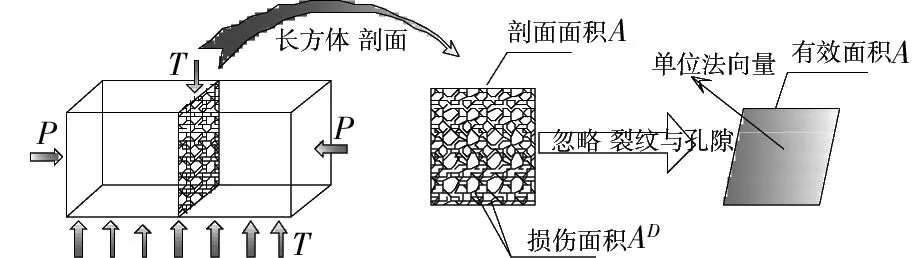
圖1　試件損傷示意圖Fig.1 Representative volume element

損傷變量D的定義AD和A的比值如下所示[10]：

(1)

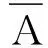
在連續(xù)損傷力學(xué)中，通常有效應(yīng)力定義描述混凝土無損部分材料的應(yīng)力，一般主應(yīng)力為整個混凝土面上的宏觀定義。有效應(yīng)力和一般主應(yīng)力與上述應(yīng)力有類似表達(dá)[11]，所有變量表達(dá)如下：

(2)

(3)

式中：上標(biāo)～為有效變量，對應(yīng)材料的無損部分；γ為塑性硬化常量；R為共軛力；a為材料參數(shù)。為了表示材料剛度退化和損傷變量之間的非線性關(guān)系，參數(shù)a取值為1。

根據(jù)一般胡克定律，可以將損傷彈性模量和有效彈性模型進(jìn)行如下定義：

(4)

式中：E為有效彈性模量；Q為硬化模量。

1.2混凝土損傷模型

本研究采用的損傷模型為Helmholtz各向同性標(biāo)量模型，并參考了Saanouni-Forster-Hatira損傷模型提出的“總自由能等效原理”，主要描述材料損傷變化過程中損傷演化及性能退化的非線性關(guān)系。

(5)

式中：ψe為材料未損傷部分的自由能；ψp為材料損傷部分自由能；κ為拉力或壓力累積塑性應(yīng)變變量。

混凝土損傷變量描述了內(nèi)部裂紋擴(kuò)展和損傷增量增加的過程，并參考了Saanouni-Forster-Hatira模型[12]，給出了具體自由能方程表達(dá)式如下：

(6)

式中：λ和μ均為無損材料的Lame常數(shù)，ρ為自由能密度參數(shù)，從而得到應(yīng)力應(yīng)變的關(guān)系如下：

(7)

式中：λ和μ均為含損傷材料的Lame常數(shù)，且有：

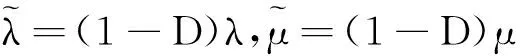
(8)

根據(jù)由能量釋放率表征的損傷驅(qū)動力的損傷演化方程為：

Y=(1-D)2α-1εe:E:εe

(9)

損傷的判斷準(zhǔn)則表示為定義在損傷屈服面內(nèi)的損傷演化規(guī)律，具體損傷屈服函數(shù)如下[13]：

(10)

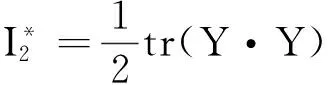
依據(jù)混凝土試驗(yàn)，給出了循環(huán)荷載作用下?lián)p傷演化規(guī)律，損傷值主要受動拉應(yīng)力影響。為了得到損傷演化規(guī)律，給出了如下?lián)p傷加載條件：

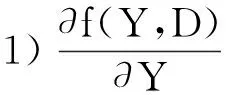
1.3擴(kuò)展到損傷累積

基于連續(xù)損傷力學(xué)，建立累積損傷預(yù)測方法，并進(jìn)行混凝土損傷演化規(guī)律的研究。建立了損傷變量與循環(huán)次數(shù)間的關(guān)系描述混凝土累積損傷發(fā)展過程，混凝土累積損傷變量需要滿足以下條件：

1)初始條件下單次循環(huán)荷載作用混凝土的損傷變量的確定；

2)循環(huán)荷載作用下每個循環(huán)次數(shù)所對應(yīng)混凝土的損傷變量值；

3)滿足混凝土破壞條件的損傷閥值。

(11)

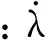
(12)

式中：a,b,s和φ為模型參數(shù)。

將公式(9)和公式(12)代入公式(11)可以得到：

(13)

通過以上公式對于累積損傷模型的推導(dǎo)，給出單次損傷變量的表達(dá)式如下[15]：

(14)

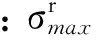
為了描述混凝土損傷演化過程，根據(jù)公式(12)給出循環(huán)荷載條件下混凝土損傷變量方程如下：

(15)

結(jié)合公式(13)，給出初始條件及混凝土損傷破壞條件下?lián)p傷變量的定義：

式中：N0是初始損傷條件下循環(huán)次數(shù)；Nf是疲勞破壞條件下循環(huán)次數(shù)；損傷破壞判斷值為DcR=1。

循環(huán)荷載作用下混凝土循環(huán)次數(shù)Nf可以表示為：

(16)

為了建立考慮循環(huán)次數(shù)累積損傷計算模型，給出了如下?lián)p傷演化方程：

(17)

2試件制備及試驗(yàn)方案

為了準(zhǔn)確獲取動力荷載作用下混凝土損傷性能的演化規(guī)律，進(jìn)行了大量混凝土試驗(yàn)研究。試驗(yàn)主要研究動靜荷載耦合作用下混凝土累積損傷特征，具體分析步驟如下。

1) 試件包括2種尺寸100mm×100mm×100mm和100mm×100mm×300mm，在24h內(nèi)完成混凝土澆筑、成型及拆模的工作，最后在混凝土養(yǎng)護(hù)室內(nèi)進(jìn)行28d標(biāo)準(zhǔn)養(yǎng)護(hù)。

2) 分別進(jìn)行混凝土試塊靜力加載測試和無損檢測：采用立方體試塊進(jìn)行混凝土靜載試驗(yàn)獲取抗壓強(qiáng)度、彈性模量和泊松比；采用ETM(Emodumete-TM) 進(jìn)行長方體試塊無損檢測，得到動彈性模量、動剪切模量等動態(tài)力學(xué)參數(shù)。

3) 荷載主要包括側(cè)向靜載、豎向靜載和動力荷載三種荷載共同作用試塊，具體加載方案為：首次在試塊兩側(cè)施加2kN側(cè)向加載力，其次逐步施加豎向靜力荷載且加載到荷載水平，進(jìn)而進(jìn)行不同加載力幅值的施加。

2.1試件制備及混凝土參數(shù)

進(jìn)行混凝土不同參數(shù)的測定及試驗(yàn)研究，同時澆筑2種尺寸混凝土試塊，采用塑料模具成型及24h后拆模，并在混凝土養(yǎng)護(hù)室內(nèi)進(jìn)行28d標(biāo)準(zhǔn)養(yǎng)護(hù)。水泥材料選用湖南水泥廠生產(chǎn)的等級為42.5的普通波蘭水泥，采用的粉煤灰產(chǎn)于湖南湘潭發(fā)電廠。試驗(yàn)中細(xì)骨料的細(xì)度模數(shù)為2.7及表觀密度為2.67kg/m3，粗骨料采用粒徑為5～25mm的石灰?guī)r碎石。混凝土試件設(shè)計的強(qiáng)度為C35，具體混凝土配合比見表1。

為了得到混凝土相關(guān)動態(tài)力學(xué)參數(shù)和靜力力學(xué)參數(shù)，進(jìn)行試塊前期測定試驗(yàn)。分別進(jìn)行立方體(100mm×100mm×100mm)靜力試驗(yàn)并得到抗壓強(qiáng)度等靜力參數(shù)，采用ETM(Emodumeter-TM)對長方體(100mm×100mm×300mm)進(jìn)行無損檢測得到動彈性模量、動剪切模量等相關(guān)動態(tài)力學(xué)參數(shù)如表2所示。

表1　混凝土配合比及耐久性指標(biāo)

表2　混凝土動靜態(tài)力學(xué)參數(shù)

2.2試驗(yàn)動力系統(tǒng)及損傷監(jiān)測技術(shù)

重載鐵路隧底結(jié)構(gòu)受力主要受由圍巖壓力產(chǎn)生的靜載和由列車荷載引起的動載共同作用。為了準(zhǔn)確模擬隧道長期列車荷載作用下隧底結(jié)構(gòu)所受力學(xué)環(huán)境，采用自制靜力加載裝置和MTS動力加載設(shè)備(圖2(a)進(jìn)行混凝土試驗(yàn)。自制裝置主要由接觸鋼板、接觸彈簧、液壓千斤頂和模型箱等部分組成如圖2(b)所示。通過液壓千斤頂和側(cè)向接觸彈簧對試塊施加靜載，模擬由圍巖壓力引起的隧道仰拱結(jié)構(gòu)的壓力作用。根據(jù)剛度相似比原理，通過測定剛度的彈簧接觸試塊模擬襯砌與圍巖之間的接觸關(guān)系。通過MTS系統(tǒng)提供一定頻率和加載力幅值的正弦荷載。

(a)MTS動力系統(tǒng)；(b)自制裝置圖2　MTS系統(tǒng)和自制裝置Fig.2 Self-developed experimental devices

近年來，EMI(Electromenchanicalimpedancetechnique)技術(shù)開始應(yīng)用到混凝土健康檢測，由于自身無模型控制和高頻激振特征等優(yōu)點(diǎn)，使其能夠敏感的探測到混凝土損傷。試驗(yàn)采用PV80A設(shè)備采集不同頻段的機(jī)電信號，通過信號換算進(jìn)而得到混凝土內(nèi)部損傷量，其中PZT壓電陶瓷片(piezoelectricleadzirconatetitanate) 黏貼于試塊表面中間。試驗(yàn)采用動態(tài)應(yīng)變采集儀(IMC)采集應(yīng)變信號，其中應(yīng)變片黏貼與混凝土試塊側(cè)面上下兩端見圖2(b)所示。試驗(yàn)所采用的2套數(shù)據(jù)采集系統(tǒng)見圖3所示。

(a)數(shù)據(jù)采集系統(tǒng)；(b)試塊測點(diǎn)圖3　數(shù)據(jù)采集系統(tǒng)和試塊測定Fig.3 Data acquisition systems and monitoring points

2.3試驗(yàn)方案

根據(jù)重載鐵路隧道底部結(jié)構(gòu)力學(xué)環(huán)境(如圖4(a)所示)，開展混凝土試驗(yàn)研究。在靜動荷載環(huán)境及恒定靜載作用下試塊損傷性能的演化規(guī)律，其中循環(huán)荷載采用頻率12Hz的正弦加載曲線。靜載水平主要反應(yīng)圍壓靜載作用，依據(jù)長方體試塊靜力破壞試驗(yàn)數(shù)據(jù)及數(shù)值計算結(jié)果，本文選取了恒定的靜載水平為0.75Fu，其中Fu表示破壞荷載力。

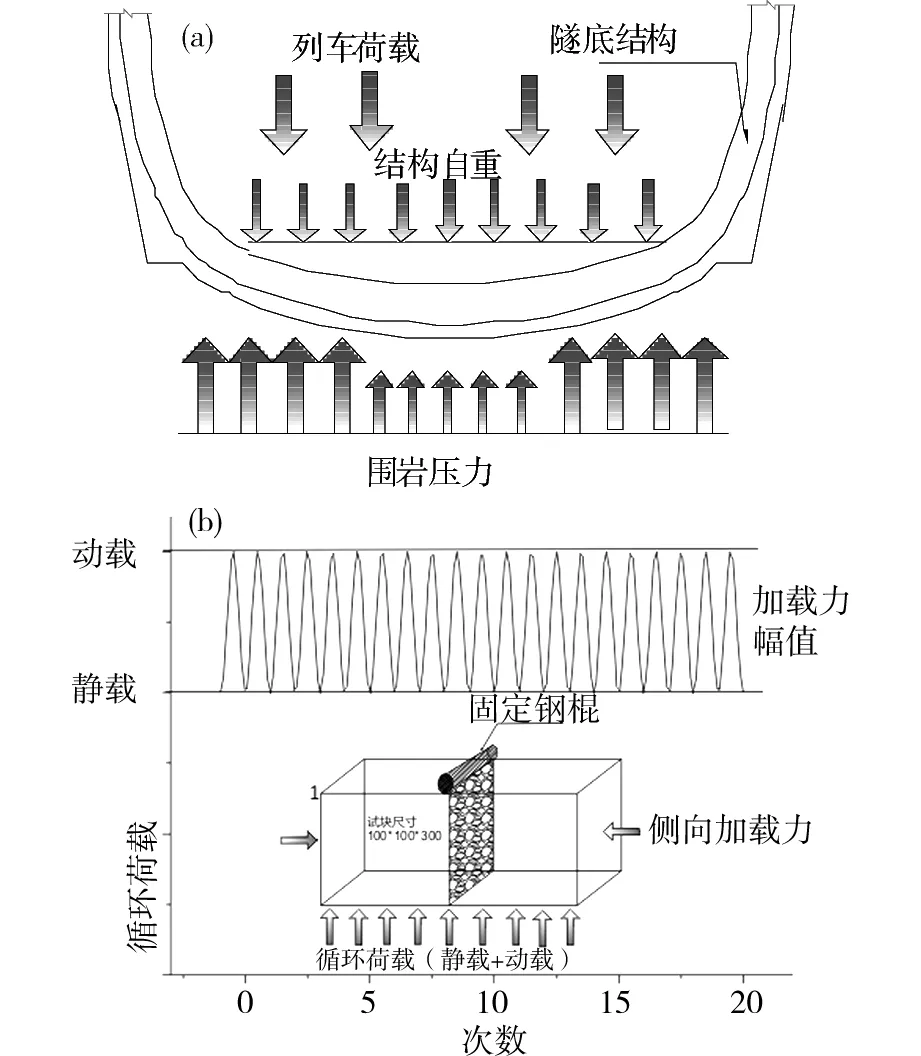
(a)隧底結(jié)構(gòu)受力環(huán)境；(b)加載力示意圖圖4　隧底結(jié)構(gòu)受力及加載示意圖Fig.4 Fatigue loading curve

列車運(yùn)行引起隧道基底圍巖的動應(yīng)力大小與諸多因素相關(guān)，如列車運(yùn)行速度、線路平順情況、軌道類型、隧道結(jié)構(gòu)型式以及以及基底狀態(tài)等，難以用簡單的計算公式來表達(dá)。鐵道部科學(xué)研究院通過對北京東郊環(huán)形的鐵道實(shí)驗(yàn)基地、廣深線上進(jìn)行的列車運(yùn)行現(xiàn)場試驗(yàn)，在試驗(yàn)數(shù)據(jù)分析和理論計算的基礎(chǔ)上，提出了路基面設(shè)計動應(yīng)力的經(jīng)驗(yàn)計算公式：

σd=0.26P×(1±0.004V)

(18)

式中：σd為路基面設(shè)計動應(yīng)力，kPa；根據(jù)重載列車軸重，P為凈軸重，kN，一般選取250，270，300和330kN；V為列車運(yùn)行速度，km/h，取100km/h。

針對列車振動荷載引起基底圍巖的累積變形問題，一方面考慮動應(yīng)力小的實(shí)際情況，另一方面考慮試驗(yàn)成果規(guī)律的對比分析，通過上述公式計算動應(yīng)力幅值分別為130，140.4，156和186kPa。由于混凝土試驗(yàn)是前瞻性的研究，本文采用動應(yīng)力幅值分別為120，160，200和300kPa。試驗(yàn)加載力幅值計算公式表示為：

ΔF=Fu-F=Aσd

式中：A為混凝土截面面積；根據(jù)混凝土試驗(yàn)受力情況，本文加載力幅值分別取3.6,4.8，6和9kN。

3混凝土試驗(yàn)結(jié)果與分析

主要研究不同振動幅值下，混凝土試件主要循環(huán)荷載作用引起的材料損傷、性能衰減及破壞整個過程變化。為了驗(yàn)證試驗(yàn)數(shù)據(jù)的正確性、可靠性及適用性，試驗(yàn)結(jié)果分析主要分以下幾個方面：

1) 靜載逐步加載過程中混凝土試件全過程損傷演化、累積應(yīng)變發(fā)展及性能衰減規(guī)律的研究。通過對靜載試驗(yàn)結(jié)果的分析，選擇適用于混凝土試驗(yàn)的豎向荷載水平工況。

2) 分析不同加載力幅值條件下，循環(huán)荷載對混凝土試件全過程損傷演化及累積應(yīng)變規(guī)律的研究。

3) 通過對試驗(yàn)數(shù)據(jù)的公式擬合并確定相關(guān)參數(shù)，進(jìn)行了混凝土試件全過程損傷演化及累積應(yīng)變規(guī)律的量化分析。

由于混凝土試驗(yàn)結(jié)果存在較大的離散型，為了在相同標(biāo)尺坐標(biāo)系下進(jìn)行不同工況的比較，采用比值形式的變量進(jìn)行實(shí)驗(yàn)結(jié)果分析。靜載階段試驗(yàn)數(shù)據(jù)的分析，采用施加荷載F與破壞荷載Fu的比值為自變量研究混凝土累積損傷演化規(guī)律。根據(jù)混凝土靜載試驗(yàn)數(shù)據(jù)，得到破壞荷載經(jīng)驗(yàn)計算公式為:Fu=0.2×fc×A, 其中fc為混凝土抗壓強(qiáng)度，A為抗壓面積。動載階段試驗(yàn)數(shù)據(jù)的分析，采用循環(huán)次數(shù)變量采用加載次數(shù)n與極限破壞次數(shù)N的比值為自變量，進(jìn)行損傷演化規(guī)律研究。

3.1不同靜載水平混凝土損傷特征研究

通過逐步施加靜載，試驗(yàn)得到隨著荷載水平提高混凝土拉應(yīng)變及壓應(yīng)變的累積變形規(guī)律如圖5所示。結(jié)果表明：隨著荷載水平逐漸增大，在[0,0.75Fu]范圍內(nèi)壓應(yīng)變和拉應(yīng)變逐漸增大，應(yīng)變值逐漸增大到100 μm；荷載水平在[0.75Fu,1]范圍內(nèi)壓應(yīng)變增長速率不變，僅僅達(dá)到混凝土極限破壞壓應(yīng)變的約0.2倍，但是拉應(yīng)變增長速率明顯加快，且表現(xiàn)出明顯的非線性特征并存在快速破壞階段。

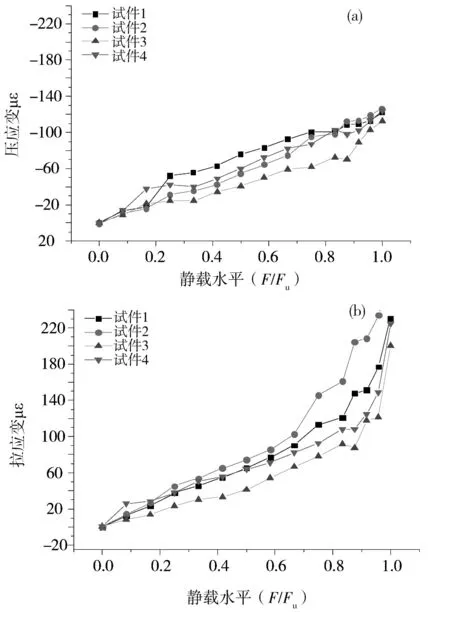
(a)壓應(yīng)變曲線；(b)拉應(yīng)變曲線圖5　應(yīng)變隨荷載水平變化曲線Fig.5 Tensile and compress strain evolution

根據(jù)混凝土應(yīng)變分析可知，拉應(yīng)變是引起材料性能衰減及破壞的主要影響因素。根據(jù)拉應(yīng)變和損傷變量的關(guān)系如圖6所示，結(jié)合試驗(yàn)結(jié)果可知隨著荷載水平的提高，損傷值逐漸增大；隨著拉應(yīng)變的增大，損傷值逐漸增大。

3.2混凝土累積損傷特征研究

給出了不同幅值條件下?lián)p傷變量和循環(huán)次數(shù)的數(shù)據(jù)曲線，以及相應(yīng)損傷演化公式的擬合曲線。如圖7(a)所示，通過損傷-次數(shù)曲線可知幅值為3.6kN條件下僅存在2個發(fā)展階段，從初期增長階段到穩(wěn)定發(fā)展階段且損傷值趨于穩(wěn)定，結(jié)果表明在循環(huán)荷載作用下未累積損傷變化和破壞發(fā)生的趨勢隨著加載次數(shù)的增加。

(a)靜載損傷曲線；(b)損傷應(yīng)變曲線圖6　損傷變化曲線Fig.6 Change of damage variable curves

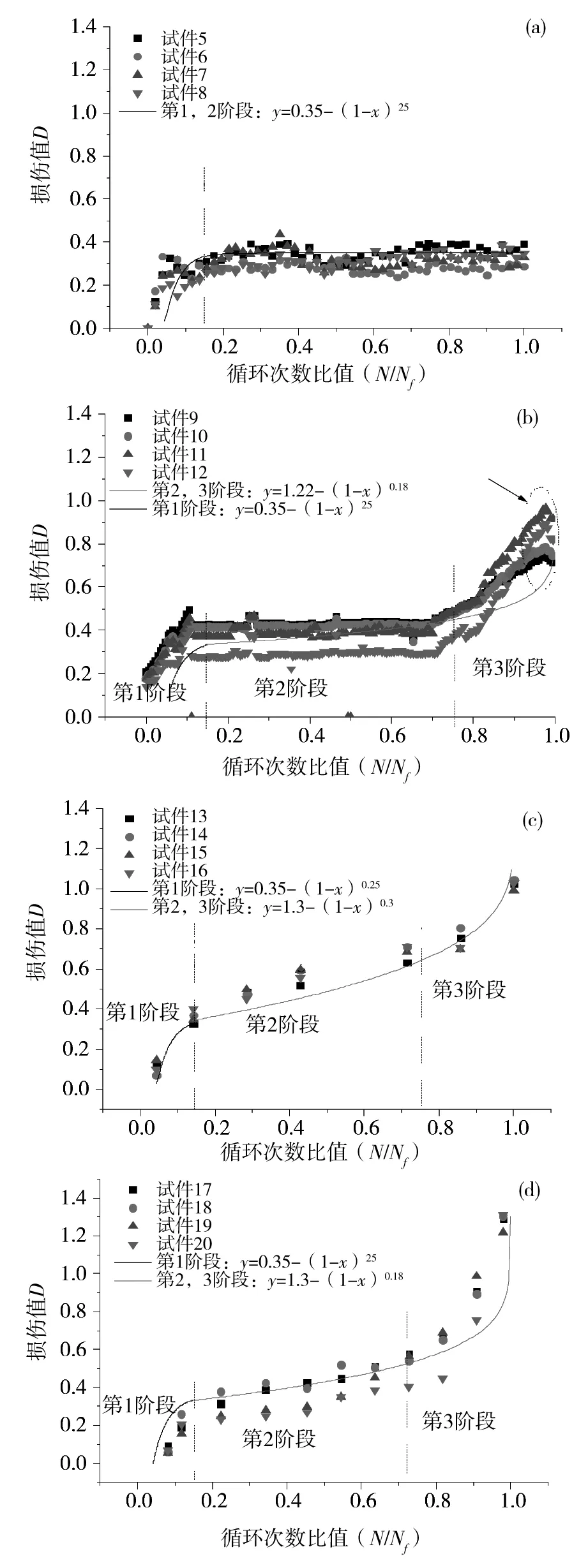
(a)加載力幅值3.6 kN;(b)加載力幅值4.8 kN (c)加載力幅值6 kN;(d)加載力幅值9 kN圖7　不同荷載水平下混凝土損傷變化曲線Fig.7 Curve of damage variable and cyclic fraction

根據(jù)圖7(b)，7(c)和圖7(d)所示，混凝土損傷變化曲線可以分為三個階段：1)初期增長階段；2)穩(wěn)定增長階段；3)快速發(fā)展階段。第1階段次數(shù)比值范圍[00.15], 當(dāng)增長損傷值達(dá)到0.3時進(jìn)入第2階段[0.150.75]穩(wěn)定增長，最后損傷值達(dá)到0.7時進(jìn)入第3階段[0.751]增長速率明顯提高并最終發(fā)生混凝土破壞。對比不同幅值條件下下混凝土損傷變化曲線可得：在幅值小于3.6kN工況下，隨著循環(huán)比值的增大，損傷變量逐漸趨于損傷值約0.6且未發(fā)生混凝土破壞。其他荷載水平條件下，加載力幅值越大，損傷值的變化速率增大且最終發(fā)生混凝土破壞。

最后給出了損傷變量和循環(huán)次數(shù)比的非線性關(guān)系，根據(jù)擬合公式和試驗(yàn)數(shù)據(jù)較好的一致性，提出適用于循環(huán)荷載作用下隧底結(jié)果混凝土的累積損傷計算公式：

(19)

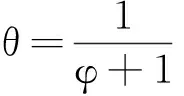
根據(jù)表3 累積損傷公式擬合參數(shù)，進(jìn)行了不同荷載水平下?lián)p傷變量的量化計算研究。公式中參數(shù)τ和參數(shù)θ用于控制損傷值及其變化趨勢。當(dāng)τ>1時，θ值增小伴隨損傷值增長率的增大；當(dāng)τ<1時，θ值減小伴隨損傷值增長率的增大。

初始增長階段損傷值主要受荷載水平的影響，不同工況下靜力加載段相同進(jìn)而損傷增長趨勢未發(fā)生變化。針對穩(wěn)定增長階段及快速增長階段，對不同幅值條件(4.8，6.0和9.0kN)對比分析可得：θ值由1.22變化到1.3，損傷值增長率逐漸提高，表明混凝土試塊加速破壞。

表3　累積損傷方程擬合參數(shù)

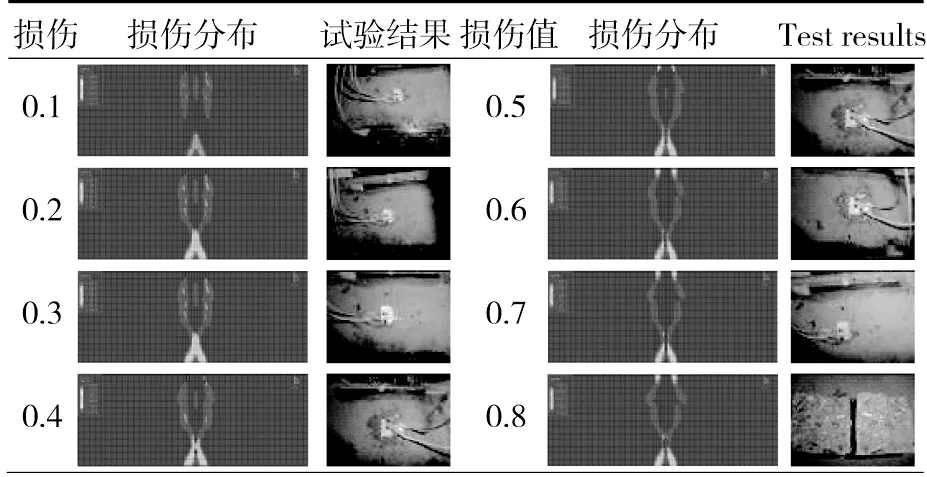
表4損傷分布云圖與試驗(yàn)結(jié)果對比

Table4Comparisonofdamagedistributionandtestresults

3.3數(shù)值計算對試驗(yàn)數(shù)據(jù)的驗(yàn)證與對比分析

基于ABAQUS/Explicit數(shù)值計算平臺，并結(jié)合試驗(yàn)給出拉應(yīng)力和損傷量之間關(guān)系曲線,以及混凝土損傷及破壞全過程中損傷演化曲線和損傷分布特征。如圖8(a)所示，對工況1中第1階段和第2階段損傷數(shù)值計算數(shù)據(jù)與理論擬合曲線的對比和其他工況第2階段和第3階段的對比，理論擬合公式與數(shù)值計算結(jié)果具有較好的一致性。

表4給出了損傷分布云圖和混凝土試驗(yàn)圖片的對比。從損傷分布云圖可以看出：初始階段損傷發(fā)生在混凝土試塊中底部；隨著損傷值的增大，損傷由下部逐漸向上發(fā)展且底部損傷值增大。

對于第1階段和第2階段前半段，即損傷值在[0,0.6]范圍內(nèi)混凝土試件表面為發(fā)現(xiàn)肉眼可見裂縫或其他損傷現(xiàn)象。損傷發(fā)展進(jìn)入第3階段，即損傷值達(dá)到0.75，在試件中間區(qū)域出現(xiàn)微裂縫并發(fā)生破壞。通過對3階段的對比，數(shù)值計算模型能夠模擬混凝土整個損傷過程包括損傷位置、損傷程度和損傷方向。

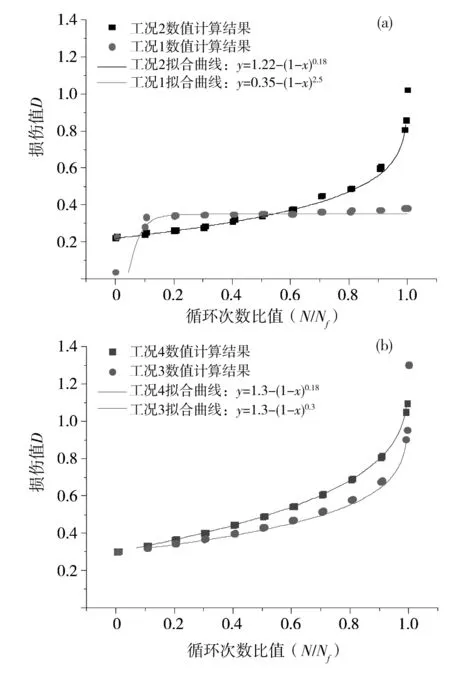
(a)工況1和工況2；(b)工況3和工況4圖8　數(shù)值計算與理論擬合曲線對比Fig.8 Comparison of damage evolution to simulation

4結(jié)論

1)基于Helmholtz自由能理論，提出考慮循環(huán)荷載的累積損傷模型，能夠描述隧底結(jié)構(gòu)累積損傷特征。通過損傷值與循環(huán)次數(shù)比值的關(guān)系曲線得出隨著循環(huán)次數(shù)的增加累積損傷非線性增長。在隧底力學(xué)環(huán)境條件下，損傷模型能夠反應(yīng)混凝土損傷演化規(guī)律，并結(jié)合試驗(yàn)數(shù)據(jù)給出不同振動幅值條件下的損傷變量的計算方法。然而該方法針對隧底結(jié)構(gòu)力學(xué)環(huán)境，具有一定的局限性。

2)為了準(zhǔn)確模擬仰拱結(jié)構(gòu)受力環(huán)境，試驗(yàn)采用自制力學(xué)環(huán)境裝置并結(jié)合MTS動力系統(tǒng)，滿足了一定靜載條件下進(jìn)行不同振動幅值作用仰拱混凝土動力試驗(yàn)研究。在靜載條件下隨著靜荷載的增大損傷值逐漸提高，當(dāng)損傷值達(dá)到0.75后混凝土損傷快速發(fā)展并發(fā)生破壞。當(dāng)靜力荷載值在0.7條件下試驗(yàn)發(fā)現(xiàn)混凝土沒有損傷累積及破壞發(fā)生。在動載條件下，分析了3階段損傷演化規(guī)律得出：相對第2階段，第1階段和第3階段損傷變化率較快。

3)根據(jù)靜載動載耦合作用下混凝土試驗(yàn)結(jié)構(gòu)，基于提出的累積損傷模型及擬合公式，得到損傷方程的相關(guān)參數(shù)并對損傷演化進(jìn)行了量化分析。通過數(shù)值計算給出了初始損傷發(fā)生位置、損傷發(fā)展方向、損傷程度及其演化規(guī)律。分別進(jìn)行了損傷演化規(guī)律和損傷分布的數(shù)值計算和試驗(yàn)結(jié)果的對比分析，并且對比結(jié)果較為理想。

參考文獻(xiàn)：

[1]WangJianxi,XiChena,LiXiangguo,etal.Influenceofheavyhaulrailwaycurveparametersonrailwear,EngineeringFailureAnalysis, 2015, 57 (1):511-520.

[2] 王春景，雷明鋒，彭立敏. 病害隧道結(jié)構(gòu)安全性評價模型與方法[J].鐵道科學(xué)與工程學(xué)報,2011,8(3):73-77.

WANGChunjing，LEIMingfeng，PENGLimin.Safetyevaluationmodelandmethodoftunneldiseasesturcture[J].JournalofRailwayScienceandEngineering, 2010,8(3) : 73-77.

[3] 丁祖德，彭立敏，雷明鋒，等.高速鐵路隧道列車振動響應(yīng)影響因素分析[J].鐵道科學(xué)與工程學(xué)報,2011,8(4):1-6.

DINGZude,PENGLimin,LEIMingfeng,etal.Analysisofinfluencefactorsondynamicresponseofhigh-speedrailwaytunnelundervibrationload[J].JournalofRailwayScienceandEngineering, 2011,8(4): 1-6.

[4] 李玉峰，彭立敏，雷明鋒,等.交叉隧道工程設(shè)計施工技術(shù)研究進(jìn)展[J].鐵道科學(xué)與工程學(xué)報,2014,11(1):67-73.

LIYufeng,PENGLimin,LEIMingfeng,etal.Researchprogressinthedesignandconstructiontechnologyofcrossingtunnels[J].JournalofRailwayScienceandEngineering,2014,11(1): 67-73.

[5] 康立鵬，施成華，彭立敏,等. 基于正交試驗(yàn)的立體交叉隧道施工影響因素研究[J] .鐵道科學(xué)與工程學(xué)報,2012,9(4):70-74.

KANGLipeng，SHIChenghua，PENGLimin,etal.Studyontheinfluencefactorsofcrossingtunnelbasedonorthogonalexperiment[J].JournalofRailwayScienceandEngineering,2012,9(4): 70-74.

[6]DoNgoc-Anh,DiasDaniel,OrestePierpaolo,etal. 2Dnumericalinvestigationofsegmentaltunnelliningbehavior.[J]TunnelingandUndergroundSpaceTechnology, 2013,37(6): 115-127.

[7]SohCK,BhallaS.Calibrationofpiezo-impedancetransducersforstrengthpredictionanddamageassessmentofconcrete.[J]SmartMaterStruct,2005,14(4):671-684.

[8]WangDansheng,ZhuHongping.MonitoringofthestrengthgainofconcreteusingembeddedPZTimpedancetransducer[J].ConstructionandBuildingMaterials, 2011(25):3703-3708.

[9]WangDansheng,SongHongyuan,ZhuHongping.NumericalandexperimentalstudiesondamagedetectionofaconcretebeambasedonPZTadmittancesandcorrelationcoefficient[J].ConstructionandBuildingMaterials, 2013, 49(1):564-574.

[10]RashidKAbuAl-Rub,Sun-MyungKim.Computationalapplicationsofacoupledplasticity-damageconstitutivemodelforsimulatingplainconcretefracture[J].EngineeringFractureMechanics, 2010,77(10):1577-1603.

[11]DuveauG,ShaoJF.Amodifiedsingleplaneofweaknesstheoryforthefailureofhighlystratifiedrocks[J].IntJRockMechMinSci,1998,35(6):807-813.

[12]SannouniK,ForsterC,HatiraFB.Ontheanelasticflowwithdamage[J].IntJDamaMech,1994,3(2):140-169.

[13]CicekliU,VoyiadjisGZ,AbuAl-RubRK.Aplasticandanisotropicdamagemodelforplainconcrete[J].IntJPlasticity, 2007,23(10):1874-900.

[14]ChabocheJL,LesnePM.Anon-linearcontinuousfatiguedamagemodel[J].FatigueandFractureofEngineeringMaterialsandStructures, 1988,11(1):1-7.

[15] 楊曉華，姚衛(wèi)星，段成美. 確定性損傷累積損傷理論進(jìn)展[J].中國工程科學(xué), 2003,5(4): 81-87.

YANGXiaohua,YAOIWeixing,DUANChengmei.Thereviewofascertaiablefatiguecumulativedamagerule[J].EngineeringScience, 2003,5(4): 81-87.

* 收稿日期：2016-01-19

基金項(xiàng)目：國家重點(diǎn)基礎(chǔ)研究發(fā)展計劃(973計劃)項(xiàng)目(2011CB013802)；國家自然科學(xué)基金煤炭聯(lián)合基金資助項(xiàng)目(U1361204)；國家自然科學(xué)基金資助項(xiàng)目(51278494)

通訊作者：彭立敏(1956-)，男，湖南澧縣人，教授，從事隧道與地下工程方面的研究；E-mail: lmpeng@mail. csu.edu.cn

中圖分類號：U25

文獻(xiàn)標(biāo)志碼：A

文章編號：1672-7029(2016)06-1091-09

Experimental study on dynamic amplitudes for cumulatedamage characteristics of tunnel invert concrete

PENG Limin, LIU Ning, SHI Chenghua

(SchoolofCivilEngineering,CentralSouthUniversity,Changsha410075,China)

Abstract:The growth of train axle load has led to an increase in dynamic loading enhancing their cumulate damage impact in the base structure of tunnel. However, the relevant theories research on dynamic performance and accumulate damage behavior are still limited and not included in current design codes. Based on the framework of Helmholtz free energy theory, this work presents a accumulate damage mode for describing the damage behavior of invert concrete due to cyclic load in tunnel environments. In order to verify the damage model and get the damage calculating method, a number of invert concrete tests under different vibration amplitudes combined were presented. The test data and numerical computing results show that the damage process is divided into three stages, initial growth stage I, slow growth stage II, and rapid growth stage III. This thesis analyzed the different stages in the damage process by fitting the nonlinear damage equation. Moreover, the critical static load level causing the failure of the specimen and the quantitative expression of the damage process is obtained. Through comparisons of the calculation results and the test results, damage are mainly distributed in the middle area, and the major maxes of damage appears around the bottom of specimen, eventually leading to destroy concrete. The evolution of initial damages appeared first at the bottom centre of specimen and new damages is forming upward progressively.

Key words:cumulate damage mode; invert concrete; cyclic load; vibration amplitudes