含初始缺陷水工混凝土的力學(xué)性能細(xì)觀(guān)數(shù)值模擬

萬(wàn)　秒　孟永東，2　盧　強(qiáng)　易軍建

(1. 三峽大學(xué) 水利與環(huán)境學(xué)院， 湖北 宜昌　443002； 2. 三峽大學(xué) 三峽地區(qū)地質(zhì)災(zāi)害與生態(tài)環(huán)境湖北省協(xié)同創(chuàng)新中心， 湖北 宜昌　443002)

?

含初始缺陷水工混凝土的力學(xué)性能細(xì)觀(guān)數(shù)值模擬

萬(wàn)秒1孟永東1，2盧強(qiáng)1易軍建1

(1. 三峽大學(xué) 水利與環(huán)境學(xué)院， 湖北 宜昌443002； 2. 三峽大學(xué) 三峽地區(qū)地質(zhì)災(zāi)害與生態(tài)環(huán)境湖北省協(xié)同創(chuàng)新中心， 湖北 宜昌443002)

摘要：在細(xì)觀(guān)數(shù)值模擬時(shí)，水工混凝土可認(rèn)為是由骨料、砂漿、界面和分布在界面單元中的初始缺陷四相材料組成，缺陷單元分布在界面單元中且符合蒙特卡洛隨機(jī)分布規(guī)律．通過(guò)對(duì)不同形狀的混凝土隨機(jī)骨料模型進(jìn)行細(xì)觀(guān)數(shù)值模擬，可知骨料形狀對(duì)細(xì)觀(guān)結(jié)構(gòu)計(jì)算的結(jié)果影響不明顯，當(dāng)缺陷單元數(shù)量是界面單元總數(shù)的1%時(shí)，隨機(jī)多邊形骨料模型的計(jì)算結(jié)果與試驗(yàn)結(jié)果最為接近．探討混凝土內(nèi)部初始缺陷含量對(duì)混凝土抗拉強(qiáng)度的影響，有利于在細(xì)觀(guān)層次揭示混凝土宏觀(guān)力學(xué)參數(shù)的非線(xiàn)性問(wèn)題．

關(guān)鍵詞：水工混凝土；初始缺陷；單軸受拉；數(shù)值模擬

水工混凝土骨料約占混凝土體積的60%～70%，骨料含量較高，澆筑成型后骨料與砂漿的交界面存在微小孔洞和微小裂紋，這些微小孔洞和微小裂紋被稱(chēng)為混凝土內(nèi)部初始缺陷[1-2]．由于水工混凝土在受拉試驗(yàn)時(shí)，采用宏觀(guān)方法統(tǒng)計(jì)所得結(jié)果與試驗(yàn)結(jié)果相比離散性較大，很多學(xué)者提出了細(xì)觀(guān)力學(xué)模型，如格構(gòu)模型、隨機(jī)粒子模型和M-H細(xì)觀(guān)模型等[3-6]．在細(xì)觀(guān)層次，混凝土被認(rèn)為由骨料、砂漿和界面三相單元組成，學(xué)者們?cè)诩?xì)觀(guān)模擬時(shí)，往往將分布在骨料與砂漿之間界面中的初始缺陷忽略或者做均質(zhì)處理，但是混凝土的破壞就是沿著這些初始缺陷展開(kāi)[7-9]．混凝土內(nèi)部初始缺陷對(duì)其宏觀(guān)力學(xué)性能的影響尚需完善[10]．因此從材料力學(xué)性能角度出發(fā)，初始缺陷單元隨機(jī)分布在界面單元中且符合蒙特卡洛規(guī)律，其力學(xué)參數(shù)滿(mǎn)足如下假定：彈性模量為極小值，泊松比為0，在受拉時(shí)即發(fā)生破壞，不考慮閉口孔隙轉(zhuǎn)化成開(kāi)口孔隙．探討混凝土中初始缺陷含量及其分布對(duì)混凝土宏觀(guān)力學(xué)性能的影響，有利于在細(xì)觀(guān)層次揭示混凝土宏觀(guān)力學(xué)參數(shù)的非線(xiàn)性現(xiàn)象．

1隨機(jī)骨料模型建模

常規(guī)骨料級(jí)配選取按照富勒提出的理想最大密實(shí)度級(jí)配曲線(xiàn)[11]計(jì)算，利用富勒級(jí)配曲線(xiàn)確定級(jí)配澆筑的混凝土可以產(chǎn)生最優(yōu)化的結(jié)構(gòu)密度和強(qiáng)度．混凝土切片時(shí)其骨料形狀為類(lèi)圓形，所以在細(xì)觀(guān)結(jié)構(gòu)選擇平面骨料形狀為圓形、正多邊形和隨機(jī)多邊形．首先按照混凝土試件模型計(jì)算出截面積為150 mm×150 mm，然后按照二級(jí)配骨料計(jì)算，小石∶中石為0.45∶0.55[11]．

試件為二維平面結(jié)構(gòu)，因此根據(jù)國(guó)外學(xué)者Walraven[12]提出的富勒級(jí)配曲線(xiàn)的三維向二維的轉(zhuǎn)換公式：

(1)

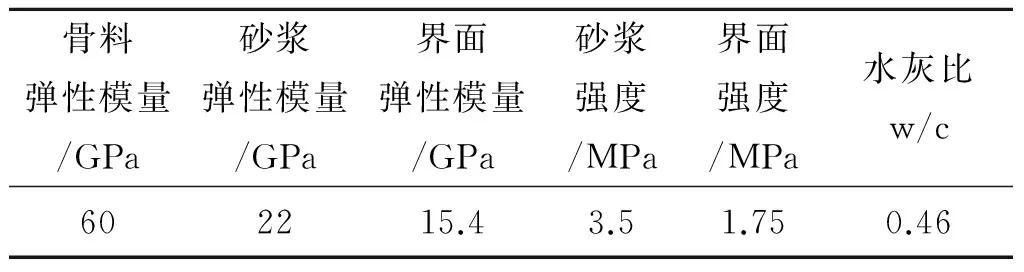
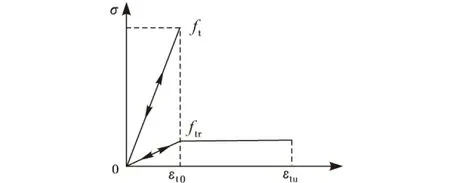
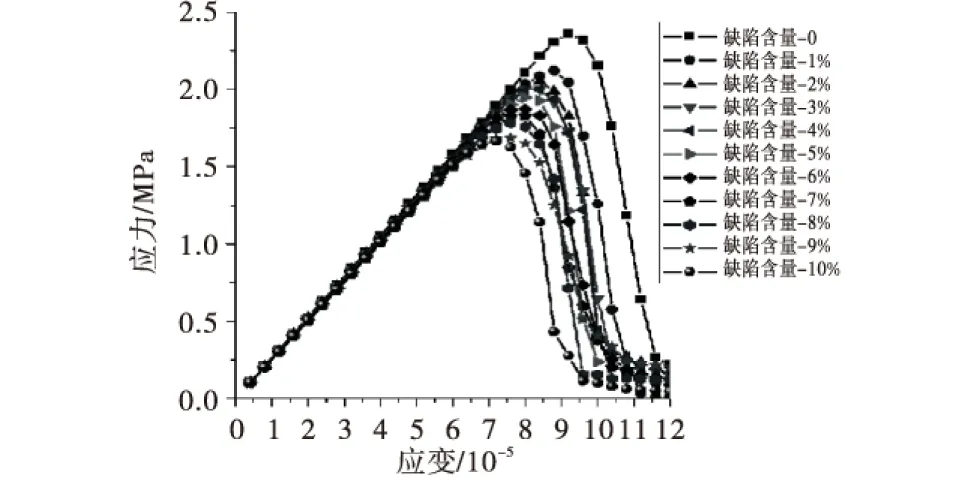
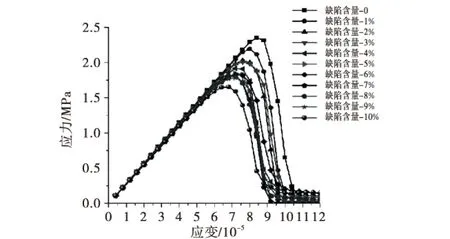
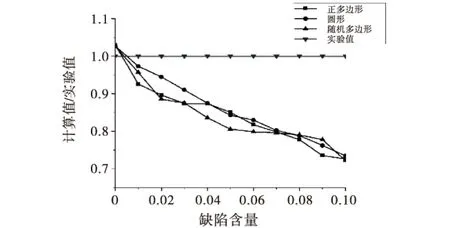
式中，Pc(D

建模步驟如下：

1)在區(qū)間150 mm×150 mm內(nèi)，根據(jù)蒙特卡洛隨機(jī)分布，由公式(1)計(jì)算各級(jí)配骨料分布概率，然后通過(guò)概率計(jì)算相應(yīng)的骨料坐標(biāo)和粒徑．

2)在相應(yīng)級(jí)配內(nèi)，生成的骨料之間進(jìn)行比較判斷計(jì)算，如骨料相交則重新生成相應(yīng)骨料的坐標(biāo)及半徑．

3)判斷骨料生成的數(shù)量是否滿(mǎn)足級(jí)配要求，若滿(mǎn)足要求則生成下一級(jí)配骨料，否則繼續(xù)生成相關(guān)骨料．

4)正多邊形骨料和隨機(jī)多邊形骨料在已經(jīng)生成的圓形骨料基礎(chǔ)上內(nèi)接，通過(guò)面積公式(2)比較判斷骨料的占有率，然后再重新生成骨料，直到滿(mǎn)足級(jí)配要求．

(2)

綜上1)～3)步完成圓形骨料的建模計(jì)算，第4)步是在前3步完成的基礎(chǔ)上，重新計(jì)算生成的骨料坐標(biāo)，完成正多邊形和隨機(jī)多邊形的建模計(jì)算．隨機(jī)骨料模型如圖1所示．

圖1　隨機(jī)骨料模型

2初始缺陷單元的定義

將所建立的隨機(jī)骨料模型進(jìn)行網(wǎng)格劃分，骨料與砂漿的交界面定義為界面層，在Ansys軟件中通過(guò)MPCHG命令修改材料屬性，假設(shè)初始缺陷單元分布在混凝土界面單元中且符合蒙特卡洛隨機(jī)分布，含缺陷的隨機(jī)骨料模型局部放大圖，如圖2所示．基于ANSYS二次開(kāi)發(fā)平臺(tái)，利用APDL語(yǔ)言編寫(xiě)宏文件，將缺陷單元隨機(jī)分布在界面單元中，每種骨料類(lèi)型選取缺陷單元量為0～10%的界面單元數(shù)，共11組樣本，隨機(jī)骨料模型整體網(wǎng)格圖如圖3所示．

圖2　不同骨料形狀初始缺陷單元分布局部放大圖

圖3　不同骨料形狀整體網(wǎng)格圖

3材料參數(shù)選取

Nagai[5]通過(guò)研究混凝土中砂漿、骨料、界面三者之間的關(guān)系，確定了砂漿的力學(xué)參數(shù)(抗壓強(qiáng)度、彈性模量、抗拉強(qiáng)度)與水灰比之間的變量關(guān)系，給出了抗壓強(qiáng)度10～60 MPa范圍內(nèi)砂漿彈性模量與砂漿抗拉強(qiáng)度的計(jì)算公式(3)～式(5)．由試驗(yàn)的水灰比[11]確定砂漿材料力學(xué)參數(shù)．

(3)

(4)

(5)

其中，Em為砂漿彈性模量，fcm為砂漿抗壓強(qiáng)度，ftp為砂漿抗拉強(qiáng)度，w/c為砂漿水灰比．

界面單元的強(qiáng)度與混凝土砂漿的材料強(qiáng)度有關(guān)，根據(jù)文獻(xiàn)[8-9]研究成果，在一般情況下，界面彈性模量為砂漿基體彈性模量的30%～70%，界面抗拉強(qiáng)度為砂漿抗拉強(qiáng)度的30%～50%．選取砂漿彈性模量的70%作為界面彈性模量，砂漿抗拉強(qiáng)度的50%作為界面的抗拉強(qiáng)度．骨料、砂漿和界面3種單元的材料參數(shù)如表1所示．

表1　數(shù)值模擬中材料參數(shù)取值

4算例分析

本算例各相材料視為彈脆性，本構(gòu)關(guān)系如圖4所示，材料參數(shù)按照表1及式(3)～式(5)計(jì)算取值．選取最大拉應(yīng)變準(zhǔn)則作為混凝土單元拉伸失效的破壞準(zhǔn)則，即單元的最大拉應(yīng)變超過(guò)閾值即認(rèn)為單元破壞；當(dāng)其未超過(guò)抗拉強(qiáng)度時(shí)采用摩爾庫(kù)倫準(zhǔn)則判斷材料是否發(fā)生剪切破壞，最大拉應(yīng)變占有優(yōu)先權(quán)．

圖4　脆性并帶有殘余強(qiáng)度的本構(gòu)曲線(xiàn)示意圖

基于ANSYS二次開(kāi)發(fā)平臺(tái)將帶有殘余強(qiáng)度的混凝土本構(gòu)，以宏文件形式實(shí)現(xiàn)，在加載過(guò)程中調(diào)用宏文件．在3種骨料形狀混凝土試件中，試件底部施加Y方向約束；兩側(cè)為自由邊界，無(wú)約束作用；上部為施加位移荷載，如圖5所示．荷載施加采用的是位移加載控制，逐級(jí)加載步長(zhǎng)0.005 mm，直至隨機(jī)骨料模型失效．隨著荷載的增加，初始缺陷單元首先發(fā)生破壞，損傷單元沿著骨料之間的界面擴(kuò)展至砂漿單元，直至模型失效．以圓形骨料為例，圖6為不同荷載下的損傷分布云圖．圖7為3種骨料形狀的軸拉失效圖．

圖5　加載示意圖

圖6　圓形骨料模型損傷演化圖

圖7　不同骨料形狀軸拉失效圖

提取不同初始缺陷含量的圓形骨料、正多邊形骨料和隨機(jī)多邊形骨料模型的應(yīng)力應(yīng)變曲線(xiàn)，如圖8～10所示，混凝土的抗拉強(qiáng)度隨著初始缺陷含量的增加而減小．將計(jì)算結(jié)果與試驗(yàn)結(jié)果[11]取比值，如圖11所示，當(dāng)不含初始缺陷時(shí)，計(jì)算結(jié)果比試驗(yàn)結(jié)果偏大，主要是因?yàn)樵诩?xì)觀(guān)層次沒(méi)有考慮缺陷單元的存在，使混凝土整體強(qiáng)度偏高，在單軸拉伸計(jì)算中結(jié)構(gòu)穩(wěn)定，較試驗(yàn)結(jié)果相比存在一定誤差；而當(dāng)初始缺陷含量為10%界面單元時(shí)，混凝土的抗拉強(qiáng)度減小了近30%，相對(duì)誤差較大，主要是因?yàn)槌跏既毕莺康脑黾邮够炷羶?nèi)部結(jié)構(gòu)在界面處變得更加脆弱，從而降低了其抗拉強(qiáng)度；當(dāng)初始缺陷含量是1%界面單元時(shí)，計(jì)算結(jié)果與試驗(yàn)結(jié)果基本一致，相對(duì)誤差在5%以?xún)?nèi)，說(shuō)明在骨料與砂漿的交界面處存在一定量的初始缺陷，其含量取1%界面單元時(shí)計(jì)算結(jié)果誤差較小；當(dāng)缺陷含量比例相同時(shí)，隨機(jī)多邊形骨料模擬的計(jì)算結(jié)果與試驗(yàn)值最為接近，主要是因?yàn)殡S機(jī)多邊形與現(xiàn)實(shí)骨料形狀更為接近，缺陷含量分布較為合理．

圖8　圓形骨料缺陷含量受拉應(yīng)力應(yīng)變曲線(xiàn)

圖9　正多邊形骨料缺陷含量受拉應(yīng)力應(yīng)變曲線(xiàn)

圖10　隨機(jī)多邊形骨料缺陷含量受拉應(yīng)力應(yīng)變曲線(xiàn)

圖11　缺陷含量與計(jì)算值關(guān)系曲線(xiàn)

5結(jié)論

通過(guò)計(jì)算不同形狀的混凝土細(xì)觀(guān)隨機(jī)骨料模型，

結(jié)果表明：初始缺陷含量對(duì)混凝土抗拉強(qiáng)度有較大影響，初始缺陷含量越高，混凝土抗拉強(qiáng)度越低．當(dāng)初始缺陷含量是1%界面單元時(shí)，計(jì)算結(jié)果與試驗(yàn)結(jié)果基本一致且相對(duì)誤差小于5%；當(dāng)缺陷含量比例相同時(shí)，隨機(jī)多邊形骨料模擬的計(jì)算結(jié)果與試驗(yàn)值最為接近．隨著初始缺陷單元的數(shù)量的增加，混凝土的抗拉強(qiáng)度逐漸減弱．本文考慮了在靜態(tài)單軸拉伸下的缺陷含量影響，但對(duì)于在復(fù)雜荷載作用下含有初始缺陷混凝土的力學(xué)性能仍有待研究．

參考文獻(xiàn)：

[1]王娟，李慶斌，卿龍邦，等．混凝土單軸抗壓強(qiáng)度三維細(xì)觀(guān)數(shù)值仿真[J]．工程力學(xué)，2014，31(3)：39-44．

[2]陳厚群．全級(jí)配大壩混凝土動(dòng)態(tài)性能研究[R]．北京：中國(guó)水利水電科學(xué)研究院，2004．

[3]杜修力，金瀏．混凝土靜態(tài)力學(xué)性能的細(xì)觀(guān)力學(xué)方法述評(píng)[J]．力學(xué)進(jìn)展，2011，41(4)：411-426．

[4]Liao K, Chang P, Peng Y． A Study on Characteristics of Inter Facial Transition Zone in Concrete[J]． Cement and Concrete Research, 2004,34(6)：977-989．

[5]Nagai K, Ueda T． Mesoscopic Simulation of Failure of Mortar and Concrete by 2D RBSM[J]． Journal of Advanced Concrete Technology, 2004,2(3)：359-374．

[6]Ollivier J P, Maso J C, Bourdette B． Inter Facial Transition Zone in Concrete[J]． Advanced Cement Based Materials, 1995(2)：30-38．

[7]唐春安，朱萬(wàn)成．混凝土損傷與斷裂-數(shù)值試驗(yàn)[M]．北京：科學(xué)出版社，2003．

[8]唐欣薇，秦川，張楚漢．基于細(xì)觀(guān)力學(xué)的混凝土類(lèi)材料破壞分析[M]．北京：中國(guó)建筑工業(yè)出版社，2008．

[9]鐘根全，李麗娟，劉鋒，等．混凝土二維隨機(jī)骨料的數(shù)值模擬[J]．混凝土，2008(9)：70-73．

[10] 杜修力，金瀏．考慮孔隙及微裂紋影響的混凝土宏觀(guān)力學(xué)特性研究[J]．工程力學(xué)，2012，29(8)：101-107．

[11] 楊木秋，林泓．混凝土單軸受壓受拉應(yīng)力-應(yīng)變?nèi)€(xiàn)的試驗(yàn)研究[J]．水利學(xué)報(bào)，1992(6)：60-66．

[12] 孫立國(guó)．三級(jí)配(全級(jí)配)混凝土骨料形狀數(shù)值模擬及其應(yīng)用[D]．南京：河海大學(xué)，2005．

[責(zé)任編輯王康平]

DOI：10.13393/j.cnki.issn.1672-948X.2016.03.010

收稿日期：2016-03-08

基金項(xiàng)目：湖北省科技支撐計(jì)劃項(xiàng)目(2015BCE079)；三峽大學(xué)研究生創(chuàng)新基金( 2015032808 )

通信作者：孟永東(1976-)，男，教授，博士，研究方向?yàn)閹r石力學(xué)實(shí)驗(yàn)．E-mail：meng@ctgu.edu.cn

中圖分類(lèi)號(hào)：TV43

文獻(xiàn)標(biāo)識(shí)碼：A

文章編號(hào)：1672-948X(2016)03-0041-04

Mesoscopic Numerical Simulation of Mechanical Properties of Hydraulic Concrete with Initial Defects

Wan Miao1Meng Yongdong1,2Lu Qiang1Yi Junjian1

(1. College of Hydraulic & Environmental Engineering, China Three Gorges Univ., Yichang 443002, China； 2. Collaborative Innovation Center for Geo-hazards and Eco-Environment in Three Gorges Area, Yichang 443002, China)

AbstractAt the mesoscopic numerical sisulation, the hydraulic concrete is composed of four-phase materials, i.e. aggregate, mortar, interfacial transition zone (ITZ) and the initial defects, accordance with Monte Carlo random distribution in the ITZ. By simulating the random aggregate model of concrete with different shapes, it is found that the aggregate shape has little effect on the results of the fine structure calculation. When the number of the initial defects is 0.01 times of the total number of ITZ elements, the results of random polygon agree well with the experimental results. To investigate the influence of the content of initial defects on the tensile strength, which is helpful to reveal the nonlinear problem of macromechanical parameters of concrete at the mesoscopic level.

Keywordshydraulic concrete；initial defects；uniaxial tension；numerical simulation