淺析幾類奇異積分算子的有界性

薛慶平 趙 輝（河南牧業(yè)經(jīng)濟(jì)學(xué)院 河南鄭州 450000）

?

淺析幾類奇異積分算子的有界性

薛慶平 趙 輝
（河南牧業(yè)經(jīng)濟(jì)學(xué)院 河南鄭州 450000）

摘 要：對具有非光滑多線性奇異積分算子有界性進(jìn)行研究。對一類廣義Morrey空間次線性算子有界性進(jìn)行探討；深入闡述了非其次空間中Marcinkiewicz積分交換算子的有界性。

關(guān)鍵詞：奇異積分算子 Morrey空間 Marcinkiewicz積分 有界性

引言

為了對非光滑核的多線性奇異積分算子進(jìn)行研究，首先對極大交換子Cotlar不等式進(jìn)行構(gòu)建，通過非光滑核多線性奇異積分算子加權(quán)有界性，對非光滑核多線性奇異積分算子有界性進(jìn)行證明。[1]

一、一類廣義Morrey空間次線性算子有界性

Morrey為了對二階橢圓偏微分方程解局部漸進(jìn)行為進(jìn)行研究，第一次引進(jìn)經(jīng)典Morrey空間。對于偏微分方程解正則性中，Morrey空間的研究具有非常重要的意義。下文就一類廣義Morrey空間次線性算子有界性的進(jìn)行探討。[2]

定理：假設(shè)＜＜∞LqR有界，同時(shí)，就任何一個(gè)存在緊支集函數(shù)() 1＜q p, 1＜∞，當(dāng)次線性算子T在(n)?，那么存在f∈并且Cpf L1 n Rx sup

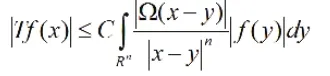
0 在 C，是絕對常數(shù)；假設(shè)Ω作為零次齊次函數(shù)，同時(shí)，有)

式中，1

0≥Ω∈α滿足任何一個(gè)下面的條件：LrS。當(dāng),p,q ,r(-1n

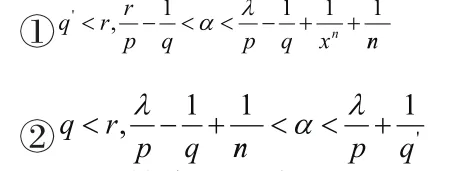
對于固定球B =B(x0,d)，存在

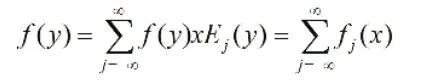
式中，,2)

E

jj-1j=B(x20,dB(x)0d

將上式進(jìn)行分解，

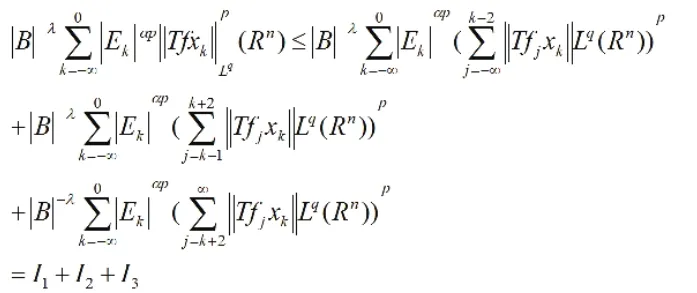
根據(jù)算子T的(n)LqR有界性，可以知道，

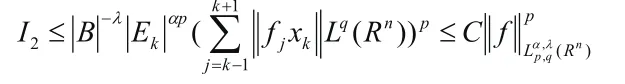
就I1，如果，那么，因此，

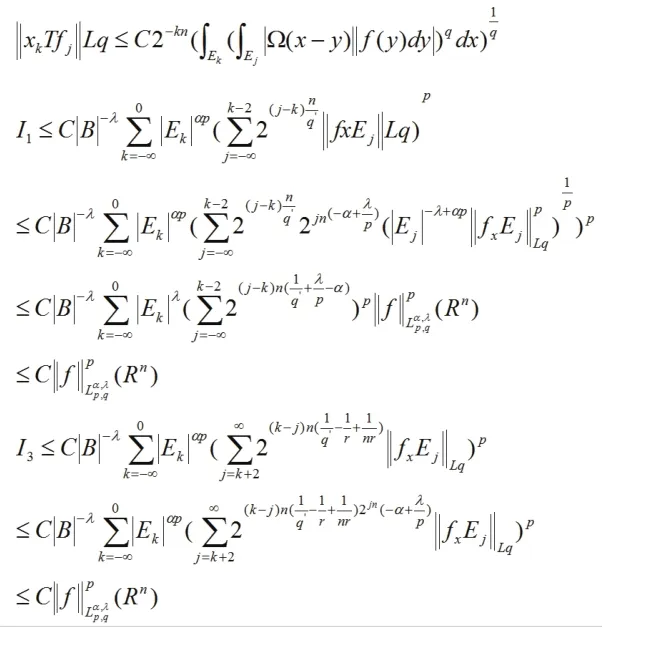
從而，證明了一類廣義Morrey空間次線性算子的有界性。

二、非齊次空間中Marcinkiewicz積分交換算子的有界性

問題提出，假定μ是在Rd上的正Radon測度，同時(shí)，與以下的增長條件吻合，就全部

x∈Rd，r＜0，存在μ(B(x,r)≤C0rn式中，C0,n為正數(shù)，同時(shí)，滿足0＜n≤d,B(x,r)表示的是x是一個(gè)半徑r的開球。就任何的x∈suup(μ)r＞0，當(dāng)μ(B(x,2r)≤Cμ(B(x,r)，那么就叫μ是倍測度。

滿足μ(B(x,r)≤C0rn的測度μ的Marcinkiewicz積分如下：假設(shè)K是定義在Rd×Rd{(x,y):x=y}的局部可積函數(shù)，并且能夠滿足以下條件：[3]

①有常數(shù)C，滿足全部的x,y∈Rd,x≠y，存在

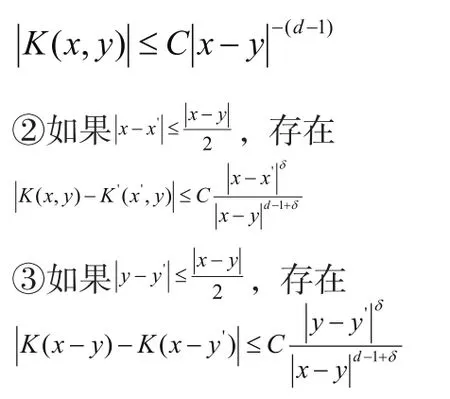
式中，0＜δ1＜。

從而進(jìn)行核K(x, y)的Marcinkiewicz積分算子的定義：

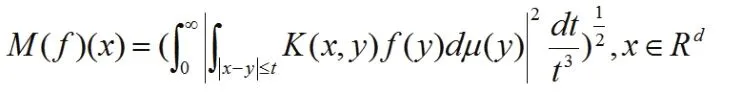
從而證明了非其次空間中Marcinkiewicz積分交換算子的有界性。

三、結(jié)束語

通過對一類廣義Morrey空間次線性算子有界性和非其次空間中Marcinkiewicz積分交換算子的有界性的研究，針對不同函數(shù)空間中算子有界性的研究，為積分算子的有界性研究提供了參考。

參考文獻(xiàn)

[1]陳曉麗，陳杰誠.次線性算子在一類廣義Morrey空間上的有界性及其應(yīng)用[C].數(shù)學(xué)年刊A輯.2011.32:705-720

[2]陳秀瓊.新型各向異性奇異積分算子的有界性[J].汕頭大學(xué)學(xué)報(bào)（自然科學(xué)版）.2014.11（15）：26-30

[3]葉曉峰，胡媛媛.非其次空間上幾類積分算子的有界性[J].華東交通大學(xué)學(xué)報(bào).2012.8（15）：68-72