基于離散八元數余弦變換的彩色圖像水印算法

吳明珠　李興民

1(廣州商學院計算機系　廣東 廣州 511363)2(華南師范大學計算機學院　廣東 廣州 510631)

?

基于離散八元數余弦變換的彩色圖像水印算法

吳明珠1李興民2

1(廣州商學院計算機系廣東 廣州 511363)2(華南師范大學計算機學院廣東 廣州 510631)

摘要定義離散八元數余弦變換及其逆變換公式，并將其應用于彩色圖像的數字水印中。首先，為了提高水印的安全性，利用Arnold變換分別對彩色水印圖像的RGBHIS六個分量進行置亂，然后將彩色載體圖像的RGBHIS六個分量整體進行離散八元數余弦變換，對置亂后的水印圖像分組并分別嵌入到載體圖像的各個中頻系數中，最后借助離散八元數余弦逆變換公式得到含水印的圖像。實驗表明，該方法不僅具有較強的抗壓縮能力，對噪聲、縮放、濾波等攻擊處理也具有較好的魯棒性和不可見性。

關鍵詞八元數離散八元數余弦變換逆變換彩色圖像水印魯棒性

0引言

隨著互聯網和多媒體技術的迅速發展，數字化產品的版權保護和信息安全問題越來越得到人們的關注。而數字水印技術則成為解決這些問題的有效手段[1]，同時也成為國內外科研人員的研究熱點[2,3]。數字水印技術主要分為空域和頻域兩個方面，然而空域水印算法因為普遍存在嵌入容量有限，對壓縮、縮放等各類攻擊的魯棒性不強[4]，所以頻域水印算法的應用相對比較廣泛。目前常用的變換域有離散余弦變換DCT，離散小波變換DWT，離散傅里葉變換DFT等，這些算法采用的彩色模型主要有RGB模型、HIS模型、YCbCr模型、YIQ模型等[5-9]。但是它們都是將各個分量獨立地進行水印嵌入，運行效率較低。隨著S.J.Sangwine等人首次將四元數理論引入到數字水印領域[10]，對彩色圖像進行多通道整體處理，不僅提高了算法的運算效率而且保留了彩色圖像各個通道間的關系，算法的魯棒性也得到很大提高[11]。之后，很多國內外研究者都將四元數理論結合各種變換提出一些新的水印算法[12-19]。Bas P等人把四元數與傅里葉變換結合，把水印嵌入到四元數傅里葉變換的平行分量中[12]，不過水印圖像失真較大。蓋琦等人首次將離散四元數余弦變換[13]引入到彩色圖像的水印技術中[14]，把彩色圖像3個分量用四元數進行整體描述，具有較好的魯棒性。江淑紅等人首次提出超復數傅里葉變換的彩色圖像水印算法[15,16]，將彩色圖像作為一個矢量整體進行描述，在一定程度上改進了灰度的水印圖像的不可見性，然而彩色水印圖像未做研究。Ce LI等人將混沌理論和四元數傅里葉變換相結合[17]，把水印信息嵌入到圖像的相位中。王向陽等人基于機器學習的思想，提出了新的彩色圖像盲水印算法[18]，把最小二乘向量機與四元數傅里葉變換相結合。馮銀波等人基于四元數離散傅里葉變換和四元數離散余弦變換提出一種雙重零水印算法[19]。

然而上述算法最多只能夠在三維空間上把彩色圖像作為一個矢量進行整體處理。如果在高于四維的情況下，四元數濾波器必然失效，因此使用高維的數學理論來處理高維數據進行水印嵌入則成為必要。而新近發展起來的八元數理論恰好為我們提供了一個新的數學工具[20-22]，使高維的數字水印技術成為可能。

本文提出了一種新的高維彩色圖像水印算法，首先定義了離散八元數余弦變換DOCT及其逆變換公式，并將其作為工具，對彩色載體圖像進行DOCT，然后將預處理后的彩色水印圖像嵌入到載體圖像的指定頻域系數中，從而實現了彩色圖像的數字水印技術。

1離散八元數余弦變換(DOCT)

本節基于八元數理論將彩色圖像的六個分量R、G、B、H、S、I進行八元數表示，然后建立DOCT公式及其逆變換公式，為后面數字水印算法的實現奠定理論基礎。

1.1彩色圖像八元數表示

1844年-1845年英國的J.I.Graves和A.Cayley發明了八元數O，它是一種非交換、非結合的八維代數[20]。

首先定義八維向量空間的坐標軸e0,e1,e2,e3,e4,e5,e6,e7，再定義此空間上的向量函數，記作f，而用彩色圖像各像素對應的R、G、B、H、S、I六個分量值作為f的虛部e2,e3,e4,e5,e6,e7上對應的數值，虛部e0,e1的數值為0。設彩色圖像f(x,y)的大小為X×Y，其中x和y指示像素在矩陣中行和列的位置，x∈[0,X-1],y∈[0,Y-1]，則彩色圖像f(x,y)的八元數表示如下：

f(x,y)=fr1(x,y)e0+fr2(x,y)e1+fi(x,y)e2+fj(x,y)e3+

fk(x,y)e4+fH(x,y)e5+fS(x,y)e6+fI(x,y)e7

(1)

其中fr1(x,y)和fr2(x,y)的值為0，fi,j,k,H,S,I(x,y)分別為彩色圖像中各個像素點的R、G、B、H、S、I分量的灰度值。

1.2離散八元數余弦變換及其逆變換

參照文獻[14]中的離散四元數余弦變換(DQCT)公式，f(x,y)對應的DOCT公式可定義如下：

(2)

其中:

(3)

同時將離散四元數余弦逆變換(記作IDQCT)的公式擴展到離散八元數余弦逆變換(記作IDOCT)中，所以f(x,y)對應的IDOCT公式定義如下：

(4)

其中f(x,y)為空間域，C(p,s)為頻率域，C(p,s)也是八元數，可表示如下：

C(p,s)=Cr(p,s)e0+Cl(p,s)e1+Ci(p,s)e2+Cj(p,s)e3+

Ck(p,s)e4+CH(p,s)e5+CS(p,s)e6+CI(p,s)e7

(5)

式中，C(p,s)用來表示彩色圖像的DOCT域對應的頻譜，Cr,l,i,j,k,H,S,I(p,s)則分別表示分布在八元數空間中的彩色圖像六個分量的頻譜。

1.3 公式的驗證

由式(1)可以看出彩色圖像f(x,y)沒有實部，有6個虛部，但是式(5)中的C(p,s)則包含了8個部分，為了確保水印嵌入之后的圖像也只有6個虛部，還是可以使用R、G、B、H、S、I六個分量來表示和傳輸，則必須要使得C(p,s)經過八元數離散余弦逆變換之后的得到的八元數也是沒有實部。否則圖像會產生失真，所以我們將計算C(p,s)所對應的逆變換，記作 f′(x,y)并對其進行驗證。

根據式(4)我們計算出f′(x,y)的各分量表達式如式(6)所示：

由式(6)可以得出兩個實部逆變換的表達式如式(7)所示：

(7)

而式(7)中的C(p,s)各個分量可以由式(2)計算得到，如式(8)所示：

(8)

(9)

2基于DOCT的彩色圖像水印算法

文獻[14]應用四元數理論在多維空間中把彩色圖像像素作為一個矢量整體進行描述，體現了圖像的色彩關聯，但是它只考慮了三個分量之間的關系。因為RGB模型和HIS模型是用不同的技術來描述彩色圖像的，所以如果我們將R、G、B、H、S、I這六個分量作為一個矢量整體來進行處理，則更能體現圖像的內部關聯性。因此我們基于高維數學工具八元數提出了一個新的基于DOCT的彩色圖像水印算法。算法的具體實現如下。

2.1水印嵌入過程

將水印信息嵌入到Cr(p,s)和Cl(p,s)中來改變兩者的值，盡管嵌入過程只是在頻率域所對應圖像頻譜的實部中進行，然而從空間域的角度來看，水印信息則是嵌入到了圖像的R、G、B、H、S、I六個分量中。這樣的嵌入技術，不但把原圖像因為水印圖像的嵌入而產生的誤差擴散到了整個圖像中，從而肉眼很難分辨出原始圖像與含水印圖像之間的區別，提高了水印算法的不可感知性。同時這種誤差還被分散到了圖像的R、G、B、H、S、I六個分量里面，那么對圖像進行各類攻擊，嵌入到圖像中的水印被破壞的程度也自然被分散到了各個分量，那么提取出來的水印與原始水印的相似程度相對較高，從而算法的魯棒性得到了加強。水印嵌入過程的算法流程圖如圖1所示。

圖1　水印嵌入算法流程圖

具體實現步驟如下：

(1) 彩色水印圖像w(x,y)分為R、G、B、H、S、I六個分量，并利用Arnold變換[22]分別對它們進行置亂，之后再用函數norm()分別計算六個分量的能量值。

(2) 彩色載體圖像f(x,y)分為R、G、B、H、S、I六個分量。

(3) 將f(x,y)的六個分量分別分成N塊，大小均為8×8，每塊都可以用一個八元數矩陣f(e)(x,y) (e=1,2,…,N)來表示。

(4) 利用選定的參數u算出六個分量所對應的DOCT，并用C(e)(p,s)表示，再提取它們的實部系數Cr(e)(p,s)和Cl(e)(p,s)，其他系數Ci,j,k,H,S,I(e)(p,s)不變。

(5) 將置亂后的水印圖像w(x,y)的六個分量分組，其中R、G、B三個分量分別嵌入到各個Cr(e)(p,s)的中頻系數中，而H、S、I三個分量則分別嵌入到Cl(e)(p,s)的中頻系數中，嵌入之后的系數記為Cr(e)’(p,s)和Cl(e)’(p,s)。具體嵌入公式如下：

(10)

其中，α是嵌入強度，值取為步驟1所計算得到的各個分量的能量值。

(6) 計算之后的新系數Cr(e)′(p,s)和Cl(e)′(p,s)與原來的Ci,j,k,H,S,I(e)(p,s)合成得到C(e)′(p,s)，再將其進行IDOCT，得出f(e)′(x,y)。

(7) 最后組合所有的f(e)′(x,y)，從而得出含水印圖像f′(x,y)。

2.2水印提取過程

水印提取過程的算法流程如圖2所示。

圖2　水印提取算法流程圖

具體實現步驟如下：

(1) 嵌入水印之后的圖像f′(x,y)分為六個分量，將它們都分成大小為8×8的N塊，分別記作f1(e)′(x,y)(e=1,2,…,N)。

(2) 載體圖像f(x,y)同樣分為六個分量，將它們都分成大小為8×8的N塊，分別記為f2(e)′(x,y)(e=1,2,…,N)。

(3) 對每一個f1(e)′(x,y) 和f2(e)′(x,y) 分別計算所對應的DOCT，記作C1(e)′(p,s)和C2(e)′(p,s)。

(4) 利用Cr1(e)′(p,s)和Cr2(e)′(p,s)計算出水印嵌入的位置，從而實現水印的提取。具體的計算公式如下：

(11)

(5) 將提取出來的水印信息的六個分量在分別進行反置亂，然后進行融合即得到提取出來的水印圖像。

3實驗結果與分析

為了檢測本算法對圖像嵌入水印的不可感知性，使用了峰值信噪比PSNR(Peak Signal-to-Noise Ratio)來進行度量。同時為了計算提取出來的水印與原始水印的相似程度，文中采用了歸一化相關NC(Normalized Correlation)系數[19]。

本算法在MATLAB7.1、Windows XP平臺上實現的。所使用的載體圖像大小為512×512的圖像。如圖3(a)、(b)所示(Lena圖像和Peppers圖像)。原始水印圖像大小為64×64的圖像。如圖3(c)所示。

圖3　彩色載體圖像與水印圖像

3.1透明性測試

將本文所提出的基于DOCT的圖像水印算法應用于圖3的樣例中，得到含水印的圖像Lena如圖4(a)所示和提取出的水印圖像如圖4(b)所示。含水印的圖像Peppers如圖5(a)所示和提取出的水印圖像如圖5(b)所示。

圖4　含水印圖像Lena與提取出的水印圖像

圖5　含水印圖像Peppers與提取出的水印圖像

從圖4(a)、圖5(a) 的結果可以看出，含水印的兩幅圖像很難感知到水印的存在。從圖4(b)、圖5(b) 與圖3(c)的對比結果可以看出，原始水印與提取出來的水印很相似。計算兩幅圖像使用該算法相應的PSNR與NC，其值分別為Lena圖像相應的PSNR=46.035，NC=1。Peppers圖像相應的PSNR=45.768，NC=0.9998。

3.2魯棒性測試

為了檢測本文提出的算法的魯棒性，本節通過對嵌入水印的2幅彩色圖像圖4(a)、圖5(a)分別進行放大一倍、添加椒鹽 噪聲(系數為0.001)、高斯濾波(系數為0.0005)、剪切1/4、 80%JPEG壓縮、旋轉10度各種不同類型的攻擊實驗。攻擊之后所提取出來的水印分別如圖6和圖7 所示。

圖6　含水印圖像Lena經各種攻擊之后提取出的水印

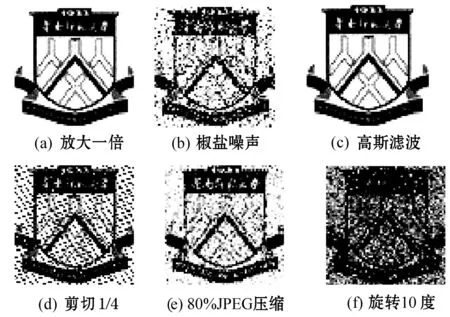
圖7　含水印圖像Peppers經各種攻擊之后提取出的水印

同時使用文獻[14]提出的算法做相同的攻擊實驗。通過分別計算這兩種算法的PSNR與NC值來進行比較，比較結果見表1所示。

表1　兩種不同算法在不同攻擊下的PSNR和NC值比較

由表1中的結果可以看出相對于文獻[14]的算法，本文的算法對縮放、噪聲、濾波、剪切、壓縮以及旋轉都具有較好的不可見性和魯棒性。

4結語

本文在RGB模型的基礎上考慮了HIS模型，首次提出了基于離散八元數余弦變換的彩色圖像水印技術，通過對彩色載體圖像進行離散八元數余弦變換來實現彩色水印圖像的嵌入，并且對縮放、噪聲、濾波、剪切、壓縮、旋轉等各類攻擊都具有較好的不可感知性和魯棒性。當然本算法在水印的提取過程中仍然需要載體圖像，所以下一步我們將研究如何在提取過程中不需要原始載體圖像，同時在彩色圖像中考慮嵌入多個水印圖像來實現版權和防篡改雙重保護。

參考文獻

[1] 蔣建國,宣曼,齊美彬.數字水印技術的研究現狀及進展[J].計算機應用,2006 (S2):60-62.

[2] 張浩,楊永健,韓鴻鶯.一種基于 DCT 的序列分組水印算法[J].計算機應用研究,2014,31(11):3473-3476.

[3] 熊祥光.基于量化和關系的圖像水印算法[J].微電子學與計算機,2013，30(9):71-74.

[4] 王丹.四元數傅立葉變換及數字水印算法研究[D].吉林大學,2013.

[5] Liu H,Kong X,Kong X,et al.Content based color image adaptive watermarking scheme[C]//Circuits and Systems,2001.ISCAS 2001.The 2001 IEEE International Symposium on.IEEE,2001,2:41-44.

[6] 吳明珠,陳瑛,李昕娣.一個基于 DWT 和改進 Arnold 置亂的數字水印算法 [J].內蒙古師范大學學報(自然科學版),2013,42 (6):687-691.

[7] 凌賀飛,盧正鼎,楊雙遠.基于 YCbCr 顏色空間的二維 DCT 彩色圖像數字水印實用技術[J].小型微型計算機系統,2005,26(3):482-484.

[8] 李諾,閆德勤.一種二維 DCT 彩色圖像數字水印的新算法[J].計算機工程與應用,2007,43(2):43-45.

[9] 李豪.基于 DWT 和混沌原理的圖像數字水印算法研究[D].浙江大學,2014.

[10] Sangwine S J.Fourier Transforms of Color Images Using Quaternion or Hypercomplex,Numbers [J].Electronics letters,1996,32(21):1979-1980.

[11] Ell T A,Sangwine S J.Hypercomplex Fourier transforms of color images[J].Image Processing,IEEE Transactions on,2007,16(1):22-35.

[12] Bas P,Le Bihan N,Chassery J M.Color image watermarking using quaternion Fourier transform[C]//Acoustics,Speech,and Signal Processing,2003.Proceedings.(ICASSP’03).2003 IEEE International Conference on.IEEE,2003,3:III-521-4 vol.3.

[13] Feng W,Hu B.Quaternion discrete cosine transform and its application in color template matching[C]//Image and Signal Processing,2008.CISP’08.Congress on.IEEE,2008,2:252-256.

[14] 蓋琦,孫云峰,王曉雷,等.基于離散四元數余弦變換的彩色圖像數字水印技術[J].光電子.激光,2009 (9):1193-1197.

[15] 江淑紅,郝明非,張建秋,等.快速超復數傅氏變換和超復數互相關的新算法及應用[J].電子學報,2008,36(1):100-105.

[16] 江淑紅,張建秋,胡波.一種超復數頻域的有意義數字水印算法[J].系統工程與電子技術,2009 (9):2242-2248.

[17] Li C,Li B,Xiao L,et al.A Watermarking Method Based on Hypercomplex Fourier Transform and Visual Attention[J].Journal of Information & Computational Science,2012,9(15):4485-4492.

[18] Wang X,Wang C,Yang H,et al.A robust blind color image watermarking in quaternion Fourier transform domain[J].Journal of Systems and Software,2013,86(2):255-277.

[19] 馮銀波,陳善學.基于四元數域的彩色圖像雙重零水印算法[J].計算機應用與軟件,2014,31(9):263-267,333.

[20] 李興民.八元數分析[D].北京大學,1998.

[21] 劉偉.八元數及 Clifford 代數在數字圖像處理中的應用[D].華南師范大學,2010

[22] 黃國恒,李興民.基于八元數的彩色掌紋特征提取與識別算法[J].計算機工程,2012,38(22):45-47,54.

收稿日期：2015-05-04。國家高技術研究發展計劃項目(2012 AA021105);國家自然科學青年基金項目(61402185);廣東省育苗工程項目(2013LYM_0118)。吳明珠，講師，主研領域：數字圖像處理。李興民，教授。

中圖分類號TP391

文獻標識碼A

DOI:10.3969/j.issn.1000-386x.2016.07.066

COLOUR IMAGE WATERMARKING ALGORITHM BASED ON DISCRETE OCTONION COSINE TRANSFORM

Wu Mingzhu1Li Xingmin2

1(DepartmentofComputer,GuangzhouCollegeofCommerce,Guangzhou,511363,Guangdong,China)n2(SchoolofComputer,SouthChinaNormalUniversity,Guangzhou,510631,Guangdong,China)

AbstractIn this paper we define the formulas of discrete octonion cosine transform and its inverse transform,and apply them in digital watermarking of colour image.First,in order to improve the security of watermark,we use Arnold transform to scramble six components of RGBHIS of colour image with watermarks.Then we exert the discrete octonion cosine transform on six components of RGBHIS of colour carrier image in whole.The scrambled watermark images are grouped afterwards and embedded into the intermediate frequency coefficients of carrier image separately.Finally by means of inverse discrete octonion cosine transform we obtain the image with watermarks.It is indicated by experiments that this algorithm has strong compression resistance capability and has better robustness and invisibility to various kinds of attacks such as noise,scaling and filtering.

KeywordsOctonionDiscrete octonion cosine transformInverse transformColour image watermarkingRobustness