流量資料抗差方法

李佳佳,包為民,2,劉可新,楊姍姍,趙麗平

(1.河海大學水文水資源學院, 江蘇南京210098；2.河海大學水文水資源與水利工程科學國家重點實驗室,江蘇南京210098)

?

流量資料抗差方法

李佳佳1,包為民1,2,劉可新1,楊姍姍1,趙麗平1

(1.河海大學水文水資源學院, 江蘇南京210098；2.河海大學水文水資源與水利工程科學國家重點實驗室,江蘇南京210098)

摘要：流量資料是洪水預報中重要的信息,它受到不服從正態分布粗差影響時,會將粗差帶入預報系統,影響預報結果精度。針對這種情況,提出了流量資料的抗差方法。該方法的關鍵就是確定適合流量資料抗差方法的權函數和權函數變量。列出兩種權函數和四種權函數變量,通過15場洪水在理想模型中的抗差效果來分析確定適合的權函數和權函數變量,并通過理想模型驗證該方法在不同誤差下的抗差效果。隨著誤差的增大,抗差效果趨于穩定,這符合抗差估計理論。

關鍵詞：流量資料；抗差方法；權函數；權函數變量；理想模型

許多洪水預報或者尚在洪水模擬階段探索的方法都是以流量資料作為基礎的；所以,流量資料的精度對于這些方法至關重要,而在觀測中流量總是帶有誤差的,尤其是粗差沒有明確的規律。而將不正常因素帶入預報系統或模擬系統,會影響系統的正確性[1- 4]。針對上述問題,提出了流量資料的抗差方法。在理想模型中分析有效的流量抗差權函數以及該方法的抗差效果,為在預報方法中的流量資料誤差處理提供新的思路。

1抗差權函數和特征量

抗差權函數是抗差方法的核心,它的選擇會密切影響抗差方法的效果。因此要選擇有效的流量抗差方法權函數。權函數的構造要能夠有效地描述系統誤差的特點。通常誤差按絕對值大小分為小誤差、粗差、極值誤差,針對不同的誤差特點,提出了兩種權函數和四種函數變量[1]

(1)

表1邵武流域使用的新安江模型參數

KWMWUMWLMCBSMEXKIKGCSCICGKEXE0.90215020800.170.4151.50.230.470.30.8970.98710.05

(2)

(3)

(4)

(5)

(6)

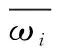
2理想模型和誤差生成模式

為了分析抗差方法的效果,本文采用了輸入、輸出、參數均為已知,且沒有誤差的理想系統。理想模型的輸入是邵武流域15場洪水的降雨、蒸發資料,參數的真值見表1。將輸入資料和模型參數帶入新安江模型計算,得到無系統誤差的流量真值。

為了對流量抗差方法分析與檢驗,需要給流量真值加上隨機誤差。隨機誤差的生成模式要考慮到抗差方法針對的誤差特點,抗差方法針對的是低頻率高強度,不服從正態分布的粗差和極值誤差,針對這些問題提出如下生成模式

(7)

式中,ei是誤差系列中發生頻率高的小誤差,ei×(N)(0,var)服從正態分布,較小,var是方差；r為隨機數；p為常數；L為粗差產生的頻率間隔。p和L的選取,可控制粗差的大小和產生頻率。所以上式產生的隨機誤差,是高頻率低強度的小誤差加上低頻率高強度的粗差。

3抗差方法

流量資料受粗差影響時,流量過程線呈鋸齒形,而在理論上流量過程線應該是一條光滑的曲線,因此對含有粗差的流量過程進行擬合成為光滑的曲線,然后用抗差權函數和特征量進行抗差,最終得到一條不受粗差影響的流量真值。為了在理想模型中反映這一過程,抗差方法的具體步驟如下：

(1)用理想新安江模型計算出流量,并將其作為流量真值Qc。

(2)根據上述誤差生成模式,將誤差賦給流量真值,得到一條含有粗差的鋸齒形流量曲線。在保證水量平衡的基礎上,將鋸齒形的曲線采用二次曲線分段擬合,選擇時段數將鋸齒形曲線分割,然后將各時段的鋸齒形曲線用二次曲線擬合,使其變成光滑的含有粗差的流量曲線，見圖1。

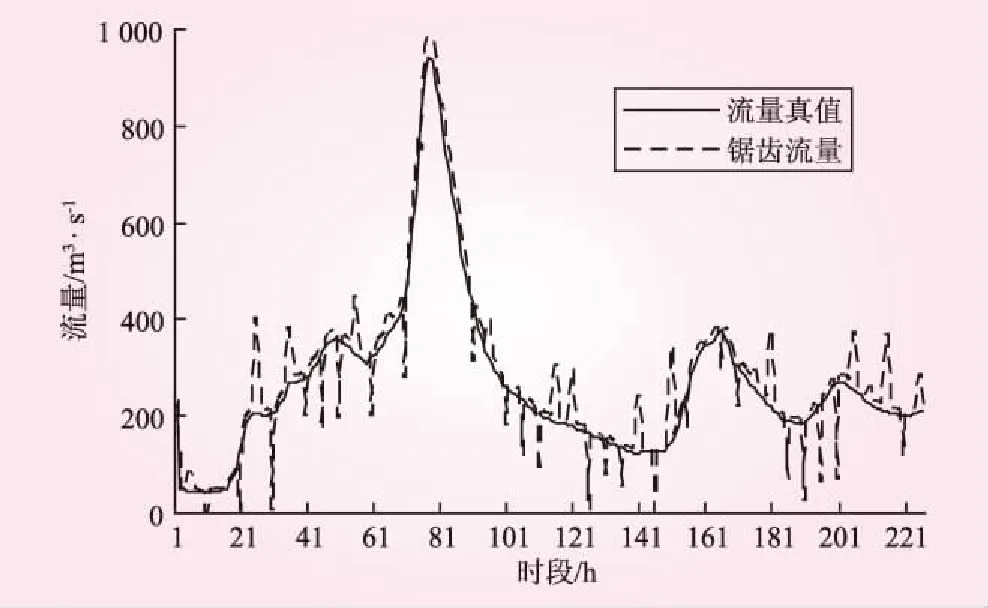
圖1　流量真值和鋸齒流量示意

(3)流量修正公式

(8)

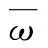
4分析與檢驗

在上述理想系統和誤差生成模式下,對15場洪水的流量真值加上誤差,然后用上述抗差方法進行修正。通過不同權函數和變量的組合可以計算出八種不同的流量修正結果。一般情況下,用流量均方差來衡量流量真值與鋸齒形流量Qjc、修正后流量Qxz的偏離程度,但由于Qjc和Qxz中異常值的存在,這些異常值應該有限制條件的評估,所以選擇流量抗差均方差來衡量該方法的效果,流量抗差均方差是一個無量綱的量,其計算公式為

(9)

(10)

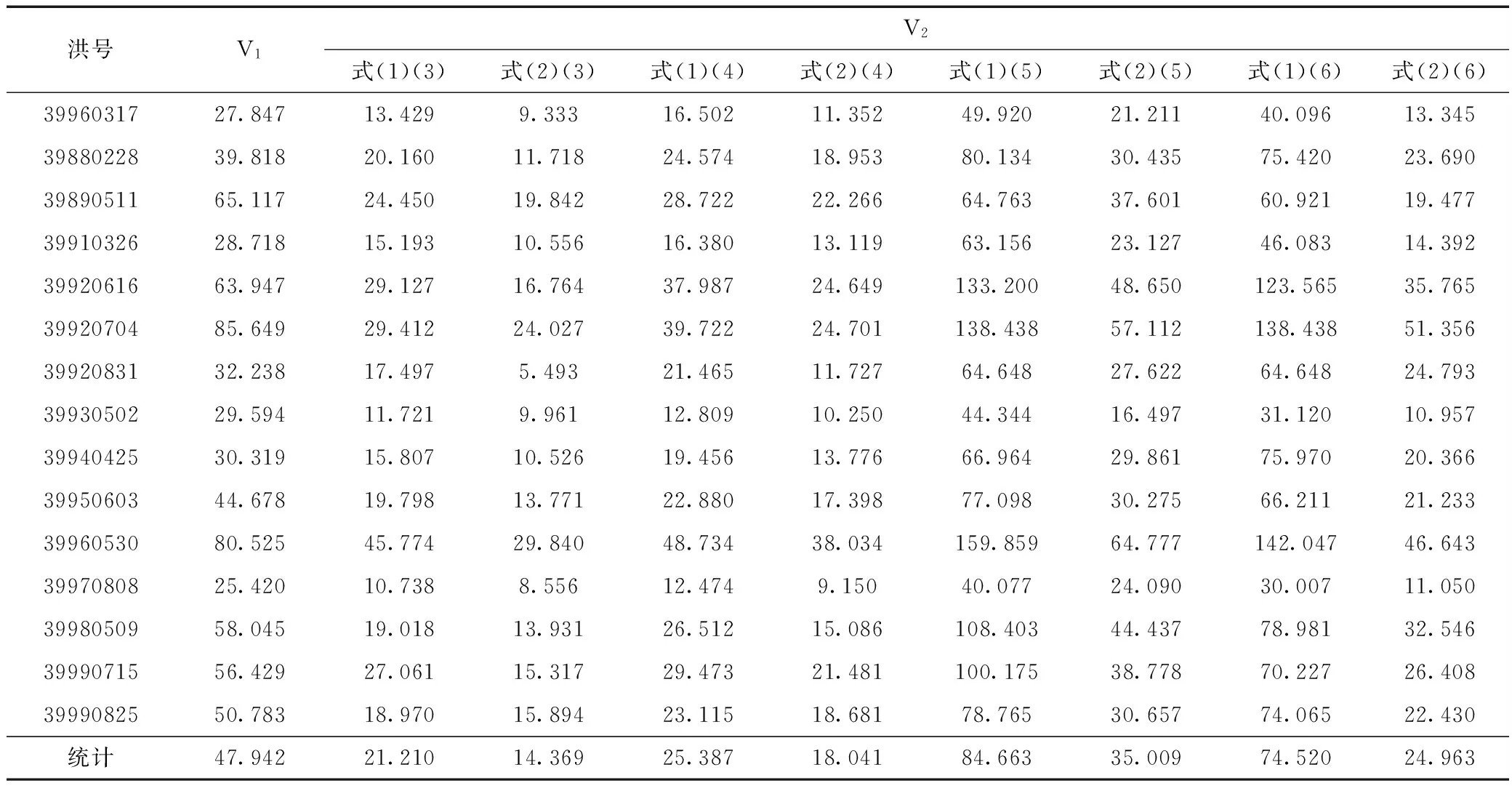
從表2分析權函數和權函數變量各種組合的抗

表2抗差結果統計

洪號V1V2式(1)(3)式(2)(3)式(1)(4)式(2)(4)式(1)(5)式(2)(5)式(1)(6)式(2)(6)3996031727.84713.4299.33316.50211.35249.92021.21140.09613.3453988022839.81820.16011.71824.57418.95380.13430.43575.42023.6903989051165.11724.45019.84228.72222.26664.76337.60160.92119.4773991032628.71815.19310.55616.38013.11963.15623.12746.08314.3923992061663.94729.12716.76437.98724.649133.20048.650123.56535.7653992070485.64929.41224.02739.72224.701138.43857.112138.43851.3563992083132.23817.4975.49321.46511.72764.64827.62264.64824.7933993050229.59411.7219.96112.80910.25044.34416.49731.12010.9573994042530.31915.80710.52619.45613.77666.96429.86175.97020.3663995060344.67819.79813.77122.88017.39877.09830.27566.21121.2333996053080.52545.77429.84048.73438.034159.85964.777142.04746.6433997080825.42010.7388.55612.4749.15040.07724.09030.00711.0503998050958.04519.01813.93126.51215.086108.40344.43778.98132.5463999071556.42927.06115.31729.47321.481100.17538.77870.22726.4083999082550.78318.97015.89423.11518.68178.76530.65774.06522.430統計47.94221.21014.36925.38718.04184.66335.00974.52024.963

差效果,可以得到以下結論：①除了式(1)式(5),式(1)式(6)的組合沒有抗差效果外,其余的6組組合抗差效果明顯。②當權函數變量相同時,式(2)的抗差效果明顯優于式(1),當權函數相同時,權函數變量的抗差效果是式(3)>式(4)>式(6)>式(5)。因此,式(2)、式(3)是抗差效果最好的組合，見圖2。分析其原因是式(1)將誤差分為三段,對于一定小的誤差,權為1,這會使得一部分粗差不能被該方法抵御,而式(2)、式(3)與其他組合相比更符合流量誤差分布特征。

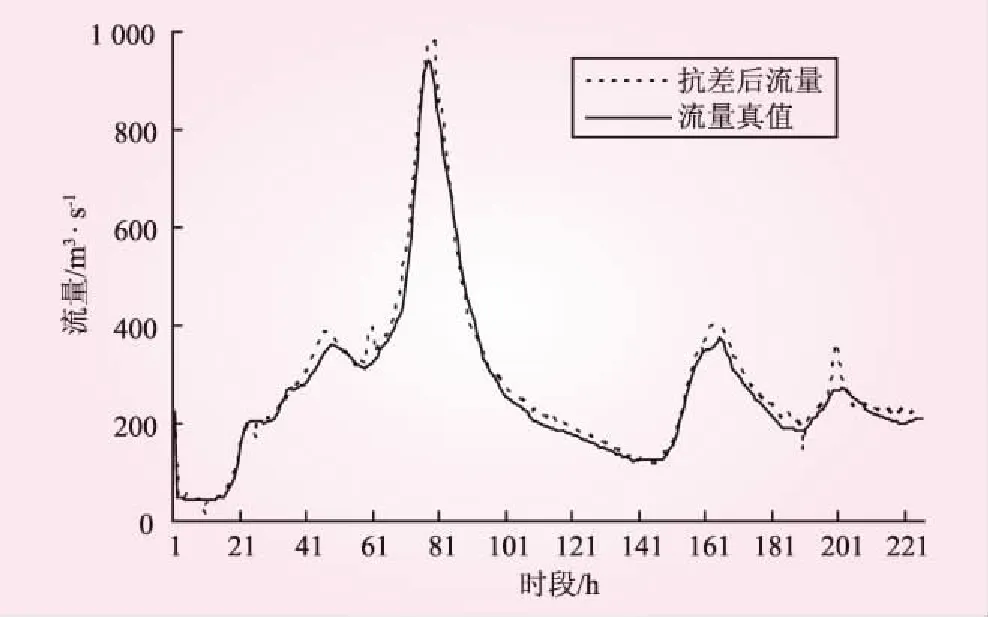
圖2　39960317次洪水流量抗差效果

在選擇合適的流量抗差權函數和變量之后,用上述抗差方法檢驗該方法在不同誤差情況下的抗差效果,這可以為使用該方法提供一個參考。因此對15場洪水分別賦予不同百分比的誤差,通過計算了解該方法對不同流量誤差的抗差效果(見表2)。

從圖3和表3可以看出,流量抗差方法對各種誤差都有一定的抗差效果。隨著平均誤差的增加,抗差前后的抗差均方差都近似線性增加,抗差后的值增加幅度較緩。隨著平均誤差的增大,殘差減小率先減小然后達到一個較穩定的范圍,這符合抗差的理論,說明該方法的設計是合理的,對抵抗流量資料中的粗差是有效果的。

表3不同誤差下的抗差效果

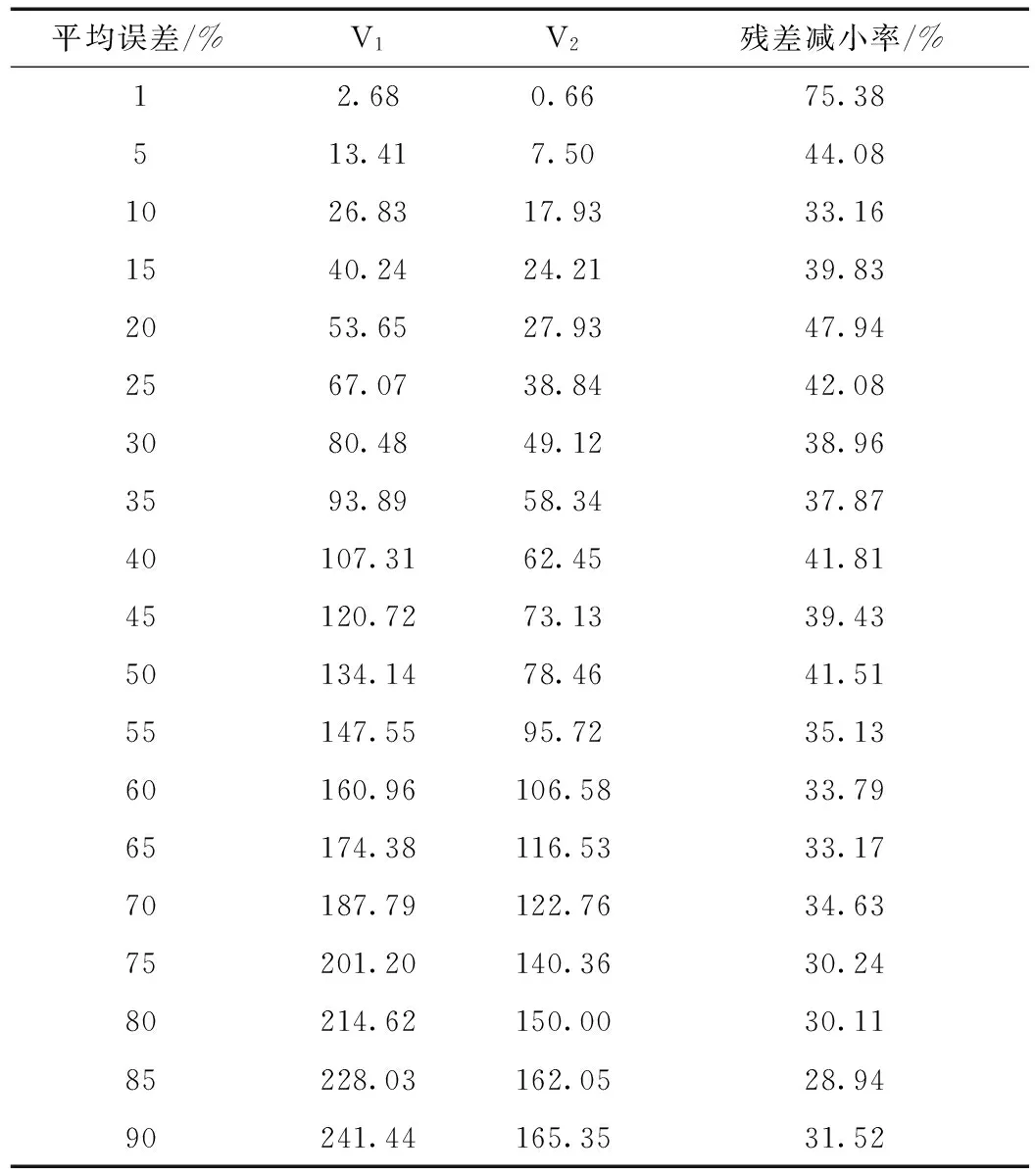
平均誤差/%V1V2殘差減小率/%12.680.6675.38513.417.5044.081026.8317.9333.161540.2424.2139.832053.6527.9347.942567.0738.8442.083080.4849.1238.963593.8958.3437.8740107.3162.4541.8145120.7273.1339.4350134.1478.4641.5155147.5595.7235.1360160.96106.5833.7965174.38116.5333.1770187.79122.7634.6375201.20140.3630.2480214.62150.0030.1185228.03162.0528.9490241.44165.3531.52

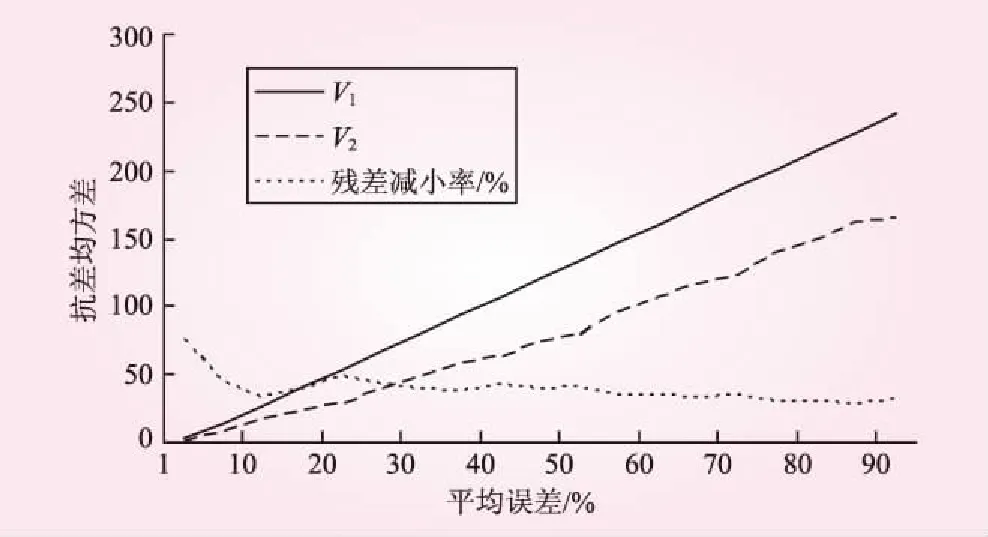
圖3　不同誤差下的抗差效果

5結語

通過在理想模型中驗證,式(2)和式(3)是適合流量資料抗差方法的權函數和變量,并驗證了該方法的可行性。該方法能有效的抵御流量資料中粗差,可以為流量過程多呈鋸齒形的水庫預報和模擬系統

提供較為準確的流量資料,且計算過程簡便。下一步的研究內容是將該方法運用到具有粗差的實際觀測流量中,如水庫,并結合預報、修正方法[6]來驗證該方法的效果。

參考文獻：

[1]包為民, 嵇海祥, 胡其美, 等. 抗差理論及在水文學中的應用[J]. 水科學進展, 2003, 14(4)： 133- 137.

[2]包為民, 瞿思敏, 黃賢慶, 等. 水文系統抗差權函數分析與檢驗[J]. 清華大學學報, 2003, 43(8)： 1127- 1129.

[3]李榮容, 吳國堯. 水庫入庫流量抗差修正研究[J]. 中國農村水利水電, 2008, (11)： 12- 14.

[4]趙超. 流域實時洪水抗差預報系統研究[D]. 南京： 河海大學, 2006.

[5]周江文, 黃幼才, 楊元喜, 等. 抗差最小二乘法[M]. 武漢： 華中理工大學出版社, 1997.

[6]司偉, 包為民, 瞿思敏. 洪水預報產流誤差的動態系統響應曲線修正方法[J]. 水科學進展, 2013, 24(4)： 497- 503.

(責任編輯陳萍)

收稿日期：2015- 05- 20

基金項目：國家自然科學基金資助項目(51279057,41371048)；國家重點實驗室專項基金(2009586412)；國家自然科學基金重大項目(51190091);中央高校基本科研業務費專項資金資助(2014B35314)

作者簡介：李佳佳(1991—),女,山西洪洞人,碩士研究生,主要從事水文水資源、水文預報研究．

中圖分類號：P337- 3

文獻標識碼：A

文章編號：0559- 9342(2016)04- 0027- 04

Robust Correction Method of Flow Data

LI Jiajia1, BAO Weimin1,2, LIU Kexin1, YANG Shanshan1, ZHAO Liping1

(1. College of Hydrology and Water Resources, Hohai University, Nanjing 210098, Jiangsu, China; 2. State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering, Hohai University, Nanjing 210098, Jiangsu, China)

Abstract:Flow data is important to flood forecasting. When it is influenced by the coarse errors which are non-normal distribution, the coarse errors will be brought into forecasting system and will cause an effect on the accuracy of forecasting results. To this question, the robust correction method of flow data is proposed, in which, the key is to determine the weighting function and variable equation. Two weighting functions and four variable equations are developed and evaluated by 15 floods in ideal model to analyze the robust effects, and the range of errors in which the method is available is testified. With the increase of errors, the robust effects tend to be steady．

Key Words:flow data; robust correction method; weighting function; variable equation; ideal model