探究高中數學解析幾何的多樣化解法

毛毳毳

（吉林省松原市長嶺縣第四中學 吉林松原 138000）

探究高中數學解析幾何的多樣化解法

毛毳毳

（吉林省松原市長嶺縣第四中學 吉林松原 138000）

在高中數學教學體系中，解析幾何是重要的組成部分，既是教學重點，同時也是教學難點，在開展高中數學解析幾何教學過程中，要尋求解題方法的多樣性和豐富性，通過尋找不同的解題路徑，可以幫助學生構建解析幾何知識體系，提升高中數學總體學習水平。本文立足高中數學教學實踐，從解析幾何具體知識入手，分析解析幾何的多樣化解決方法。

高中教學 高中數學 解析幾何 解法

解析幾何是高中數學的重點也是難點，也是訓練提升學生邏輯思維和空間想象能力的重要工具，備受高中數學教育工作者的重視[1]。在解析幾何學習過程中，往往有多種思考方式，運用綜合分析法和體系性分析法，都可以解決問題。在教學實踐中，教師要注重利用解析幾何知識，激發學生學習自主性和學習自信心，要利用幾何知識提升自身數學知識應用水平。

一、多樣化解決幾何最值問題

在高中數學解析幾何學習過程中，最常見的問題是求最值問題，屬于高頻考點，同時也是學生學習的關鍵和基礎。因此，通過尋求解析幾何最值問題的多樣化解決途徑，可以有效提升高中生解析幾何綜合應用能力，提高幾何教學實效[2]。

1. 充分利用幾何圖形的對稱性特點

在高中數學解析幾何解題過程中，應用對稱性解題方法，有著深刻的理論依據，當圖形兩邊之差或者兩邊之和實現三點共線的時候，可以實現其數值的最大化，運用這種思維，可以實現快速高效解題。

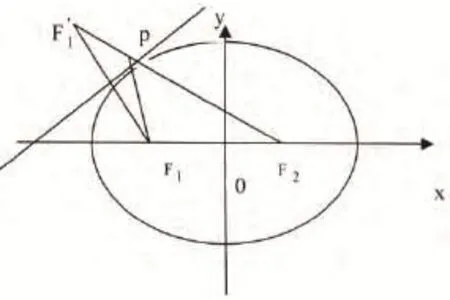
2. 綜合利用多種解題方式

除了利用圖形的對稱性外，還可以應用多種其他方法，解決解析幾何最值問題，比較常用的方式是利用圓錐曲線定義方式求解最值問題，通過提取關鍵信息，實現相關數值的量化和轉換，利用已知數值和條件，實現最值問題的有效求解[3]。此外，還可以利用函數值解決解析幾何中的具體問題，通過函數法，可以有效提升解析幾何問題的解題效率，特別是在最常見的求最值問題當中，應用代數思想，可以將抽象的圖像轉化為具體的數學公式，進而求解問題。

舉例來說，常用的函數解題方法包括二次函數法、均值不等式法等等，都是行之有效的解析幾何解題方式，可以實現多樣化解題的目的。對于很多數學能力比較強的同學，教師還可以強化教學引導，引導學生利用均值不等式原理，解決解析幾何問題。此外，還可以運用距離公式，提升解題效率和解題方式。因此，通過總結以上解題方式，不難看出，要想解決解析幾何問題，有著多種多樣的方法，最為重要的是掌握其中的原理，進而迅速發現“題眼”，找到解決問題的突破口，實現高效、快速解題，在應用多種方式解決解析幾何問題的時候，要仔細分析題意，做到心中有數，選擇最為熟練和快速的解題方法，通過反復練習，提升對于解析幾何問題的敏感度，提高解題速度，最終實現高中數學學習水平的有效提升，構建自身知識體系。

二、應用三角函數知識豐富解析幾何解法

在解決解析幾何問題的時候，三角函數知識是重要的突破口和切入點，結合幾何問題的特點，利用函數知識，可以實現高速解決。在應用三角函數解決幾何問題的時候，還是要根據具體的題目特點，很多時候應用三角函數知識解決解析幾何問題并不便捷，但是卻可以提供一種不同的思路，對于很多問題，運用三角函數解決是比較方便的[4]。教師在教學過程中，要注重教學引導，學生在選取多樣化解題方法之前，首先要了解清楚題干內容和題干要求，真正弄懂問題，根據題目中所考察的知識點，尋找最佳解決方法。

三、應用向量知識解決解析幾何問題

在高中數學解析幾何問題解決過程中，教師可以引導學生，利用向量知識解決解析幾何問題。從知識特點來看，解析結合中的各種元素，包括直線、線段、橢圓、曲線等，都是在坐標軸內呈現，這給向量知識的應用提供了廣闊的空間，在解析幾何知識結構中，很多幾何問題，包括平移、全等、相似等，都可以通過向量知識表現出來，運用向量知識，可以實現解析幾何問題的多樣化解決。

四、運用數列知識解決解析幾何難題

分析各地歷年高考題目，很多地方都出現了解析幾何知識與數列知識結合的問題，而且都是以最后壓軸大題的方式出現，難度較高，具有較高的考試區分度，如果能有效掌握這種解題方法，可以有效提高學生學習層次和考試成績。在高中數學教學實踐中，教師要注重解析幾何知識和數列知識的有機結合，從概念、性質等方面入手，尋求知識之間的有效銜接，打通高中數學學習脈絡，厘清知識點之間的內在關系，為學生解決解析幾何問題提供更多的方式和路徑，以提升學生知識應用的靈活程度，提高學生解題能力[5]。如此一來，不管是對于提升學生考試成績還是知識運用能力，都具有重要意義。

結語

綜上所述，在高中數學教學體系中，解析幾何是重要的組成部分，學習好解析幾何，不僅可以提升學生幾何解題能力，更為重要的是，能夠鍛煉學生的邏輯思維和空間想象能力，切實提高學生的數學水平。在高中數學解析幾何教學過程中，教師要注重教學引導，鼓勵學生從不同角度思考解析幾何問題，通過深入淺出分析，探索多樣化的解題方法，實現解題效率的提升，進而構建自身數學知識體系，提高解析幾何學習的邏輯性和體系性。

[1]宮前長.關注幾何性質喚出簡捷解法——例談解析幾何題的幾何剖析與教學啟示[J].中學數學,2010(10):52-54.

[2]鐘水兵.一類高考試題解法探究——解析幾何與幾何面積的交匯題的處理策略[J].中學數學雜志：高中版,2012(5):58-59.

[3]黃偉軍.解析幾何中的定點、定值與最值問題解法揭秘[J].廣東教育：高中版,2012(1):20-22.

[4]王貴文.一類高考解析幾何題的解法探究[J].數學教學研究,2011,30(10):43-44.

[5]過江英.一道意濃的解析幾何題[J].語數外學習（數學教育）,2013(6):28-28.