靈活運用假設法，讓分數應用教學更靈活

萬 麗

（江西南昌市城南小學 江西南昌 330000）

靈活運用假設法，讓分數應用教學更靈活

萬 麗

（江西南昌市城南小學 江西南昌 330000）

假設法是我們進行科學研究的一種重要思維方式，也是一種重要的數學思想方法，在數學領域中有著及其廣泛的應用。縱觀整個小學數學教學過程，當我們面對各種錯綜復雜的數學問題（尤其是分數應用類問題）束手無策時，往往是“假設法”給了我們“柳暗花明又一村”的希望。靈活運用假設法可以將一些抽象的條件具體化，復雜關系明朗化；可以幫助教師講清一些復雜題目之間的數量關系，使得我們的教學更加生動有效；亦可幫助學生拓展思維、加深理解，提高分析解決問題的能力，從而有效培養其主動探究的意識和創新精神。為了全面搞清假設法在小學分數應用類問題中的各種類型，在教學中有效滲透假設的數學思想，從而有效促進小學數學教學工作，本文將就假設法在小學分數應用教學中可能出現的各種類型展開較為細致的分類并對其進行論述。

假設法 分數應用 細致分類與論述

教學中，教師要充分引導學生大膽去假設。另外，需要明確的是假設法的運用必須得貼近學生的生活實際，并且要方便計算。假設的目的不僅僅是為了解決問題，更重要的是讓學生的思維不局限于老師和課本講過的方法內容當中，開創發散思維和求異思維，從而培養其勇于探索、敢于創新的精神，使學生的創造能力更好地得以開發。

為了能在教學中有效地滲透假設的數學思想，讓廣大學生能夠更好地掌握運用假設法，明確什么時候該假設，什么時候不需要假設，讓假設法充分為我所用，首先，作為教師我們必須得熟知假設法在小學教學中的各種類型。下面僅根據本人在教學實際中的點滴體會，結合具體實例就假設法在小學分數應用教學中可能出現的各種類型展開較為細致的分類并對其進行論述，以期能和各位同仁共勉。

一、只含其率，不見其量

當題目條件中只有分率而沒有具體數量，讓我們比較兩個量之間的關系時，教學中我們通常采用假設法（假設法在此類題目中運用得極為廣泛）。

教學中，當某個數量連續出現幾次變化，條件中又只給出變化前后這個數量所對應的分率，而沒有具體數量時，我們通常采用假設法。教師可引導學生假設原來這個數量為一個具體值（這個值得符合學生生活實際、便于計算），然后按著給定條件的變化規律，尋找最終結果與原先數量之間的關系即可。

從以下題目的解法對比中，我們可以更清楚地看出假設法在此類題目教學中的優勢：

[解析]教學過程中，我們可引導學生采用三種方法求解。

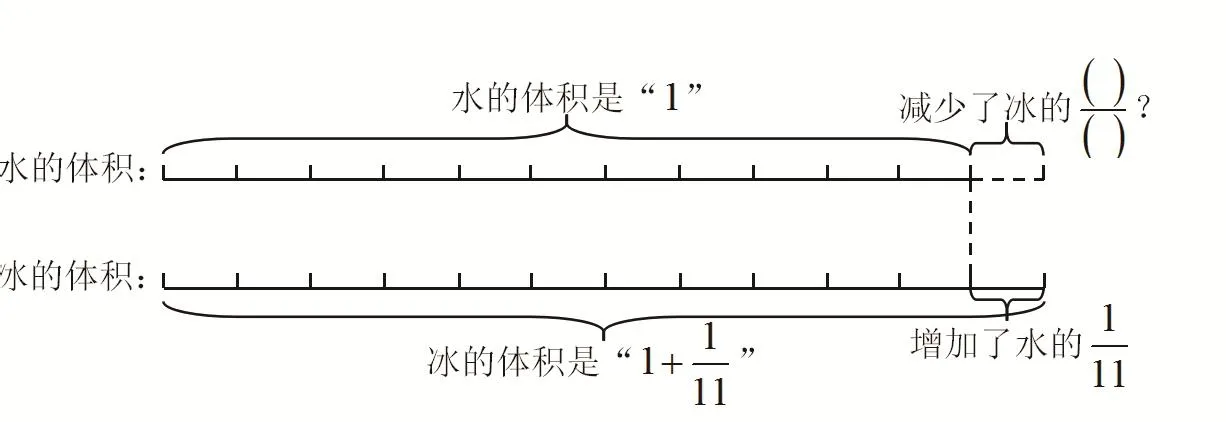
方法一（線段圖法）：

把水原來的體積看做單位“1”，水結成冰時，它的體積增加了原來的此時冰的體積變成了冰化成水后體積從”變回到了“1”，體積減少了因此，冰化成水后，它的體積減少了冰的。教學實踐表明，學生因對線段圖的畫法存在一定困難，而且根據線段圖分析解答問題的能力不強，所以此法收效甚微。

方法二（份數法）：根據“水結成冰時，它的體積增加了原來的”，我們可以把水原來的體積看做11份，增加了（份），冰就變成了11+1＝12（份），冰化成水后，體積又從12份變回到了11份，減少了1份，即體積減少了冰的對比“線段圖法”，“份數法”簡單了很多，但相對基礎一般、甚至較為薄弱的學生來說此法對于思維的邏輯性要求比較高，掌握起來并不怎么得心應手。

方法三（假設法）：假設水結成冰時，水原來的體積為11立方分米（假設11立方分米不僅符合生活實際，而且可以方便計算），則結成冰后體積變成了（立方分米）。因為冰化成水后，體積肯定從12立方分米變回到11立方分米，所以它的體積減少了冰的對比“份數法”，“假設法”在此題中的靈活運用，顯得更加直接形象，可以將抽象的分數應用題瞬間變得具體化，使廣大學生解答起來更輕松，理解起來更加深刻明了，亦可幫助我們有效突破教學難點，提高課堂教學效率。因學生更加習慣于運用具體數量解題，所以對比三種解法“假設法”最有優勢，廣大教師同仁們不妨一試。

二、式中含字母，得數比大小。

當給出的式子中有字母出現，比較的又是幾者得數之間的大小關系時，教學中我們可引導學生使用假設法。例如：

a是一個非0自然數，在下列各式中，（ ）的得數最小。

當然，此題可根據“除以一個數就等于乘以這個數的倒數”把除法全部變為乘法，再根據“被乘數一樣，乘數越小所得的積越小”來解。但如果我們的學生能夠靈活地運用假設法，哪怕不知道或沒有想到“被乘數一樣，乘數越小所得的積越小”也同樣能夠很方便地得到答案，而此法對于基礎較為薄弱的學生也同樣奏效。比如教學時，我們可以引導學生假設a=1，再分別求出四個選項的結果就很容易得到正確答案B。

值得一提的是，假設法幾乎在解答此類問題過程中均可被采用，可以說是解決此類問題的“萬能藥”，因此非常值得我們大家在教學中借鑒推廣。

三、未知藏等式，大小需待定

當題目沒有給出具體數量只給出幾個量之間關系的等式，并讓我們找出這些量之間的大小關系時，教學中我們通常采用假設法。例如：

⑴且A，B，C都不等于0，請排列出A，B，C的大小。

⑵買同樣價格的一支筆，甲用去了他所帶錢的乙用去了他所帶錢的判斷甲、乙誰帶去的錢多？

[解析]根據“買同樣價格的一支鋼筆”，可以知道甲所帶錢的就等于乙所帶錢的寫成等式，即甲由此我們可以假設甲

當題目沒有給出具體數量只給出幾個量之間關系的等式，并讓我們找出這些量之間的大小關系時，教學中，我們不妨引導學生假設該等式就等于1（或其它符合實際、方便計算的數都行），然后分別求出等式中的每個量，就能很方便地排列出這些未知量的大小。教學實踐表明，絕大多數學生對于運用假設法解答此類題目，掌握理解起來顯得得心應手。

總之，在小學分數應用教學中，教師要實時注重對學生假設數學思想方法的培養，并將其內化為學生的一種能力。因為，靈活運用假設法不但能夠輔助我們的課堂教學，幫助我們理清一些復雜的數量關系，使我們的教學更加生動有效，而且還可以幫助學生打破固有的思維模式，充分拓展思維空間，加深對題目意思的理解，從而提高分析解決問題的能力，繼而形成主動探究的意識和勇于創新的精神。