海底陣型校陣誤差評估方法*

張永超　徐國貴

(91388部隊　湛江　524022)

?

海底陣型校陣誤差評估方法*

張永超徐國貴

(91388部隊湛江524022)

摘要海底陣的測陣方法有絕對測陣和相對測陣。絕對測陣耗時長、精度高；相對測陣耗時雖短，但精度稍低。綜合利用這兩種測陣方法，文中給出了三種評估海底陣型測陣誤差的方法，為海底陣型尋找一個合理的測陣航行路線提供評估依據。方法一為推算誤差，利用誤差傳遞的方向和大小，畫圖標注誤差級別，近似計算各級別處定位誤差；方法二為建模仿真解算誤差；方法三為誤差公式計算誤差。通過分析三種評估方法計算的海底陣型各點誤差大小及誤差傳遞過程中的變化規律，可知三種方法在反映誤差傳遞過程中的變化規律相同，方法一直觀快捷，方法二結果可靠性強。

關鍵詞海底陣; 測陣校陣; 測陣誤差; 評估方法

Class NumberTB565

1　引言

基于海底水聲基陣的固定式測量系統，具有測量范圍大、受海況影響小、可長時間連續工作、對水下運動目標無影響、通信容易實施等特點，可用于海區環境的長期監測、海底地形地貌測量與海底地質勘察、水聲導航與動力定位、水聲通信與水聲遙控遙測等領域，此外，在軍用上可以滿足實戰條件下全系統、多平臺試驗任務，具有較高的綜合使用效益[1]。

鋪設較大規模的海底陣，其測陣校陣顯得尤為重要，目前的測陣方法為絕對測陣和相對測陣[2]。絕對測陣，耗時很長，但測量精度高；相對測陣，耗時雖短，但精度稍低。綜合利用這兩種方法，可以找出一種較為合適的測陣校陣航路，使得海底陣型校陣費時少、精度高。優選海底陣型校陣航路時，所需要的是能夠直觀快捷的排選方式，而對陣型校陣精度要求不高，但計算校陣中定位誤差的方法必需合理反映誤差變化情況。

文中給出三種評估海底陣型校陣中定位誤差的方法，方法一，即推算誤差，畫圖標注并利用誤差傳遞的方向和大小，近似計算待測點誤差；方法二，即仿真建模解算誤差，將陣型建立坐標系，通過已知點坐標(包含誤差)利用球面交匯公式計算其他位置潛標各點；方法三，即誤差公式求解誤差，利用誤差公式，帶入相關數據計算待測點誤差大小。通過三種方法計算的結果，分析它們的優缺點，為海底陣型校陣過程中，尋找合理的海底陣型校陣航路提供評估依據。

2　測陣原理

2.1絕對測陣

絕對測陣，即試驗船在GPS的引導下，按預定的航路航行到預定的數據錄取點時發射測陣詢問測距聲脈沖，并獲取所要潛標的測距值及測量船相應位置GPS坐標數據，每個數據錄取位置連續錄取若干幀數據，利用球面交匯的原理，解算出海底潛標的坐標。解算前需要對數據進行處理：各測量點相鄰連線成直角定位精度較高，對所求解取平均[3～4]。

航行測量過程如圖1所示。

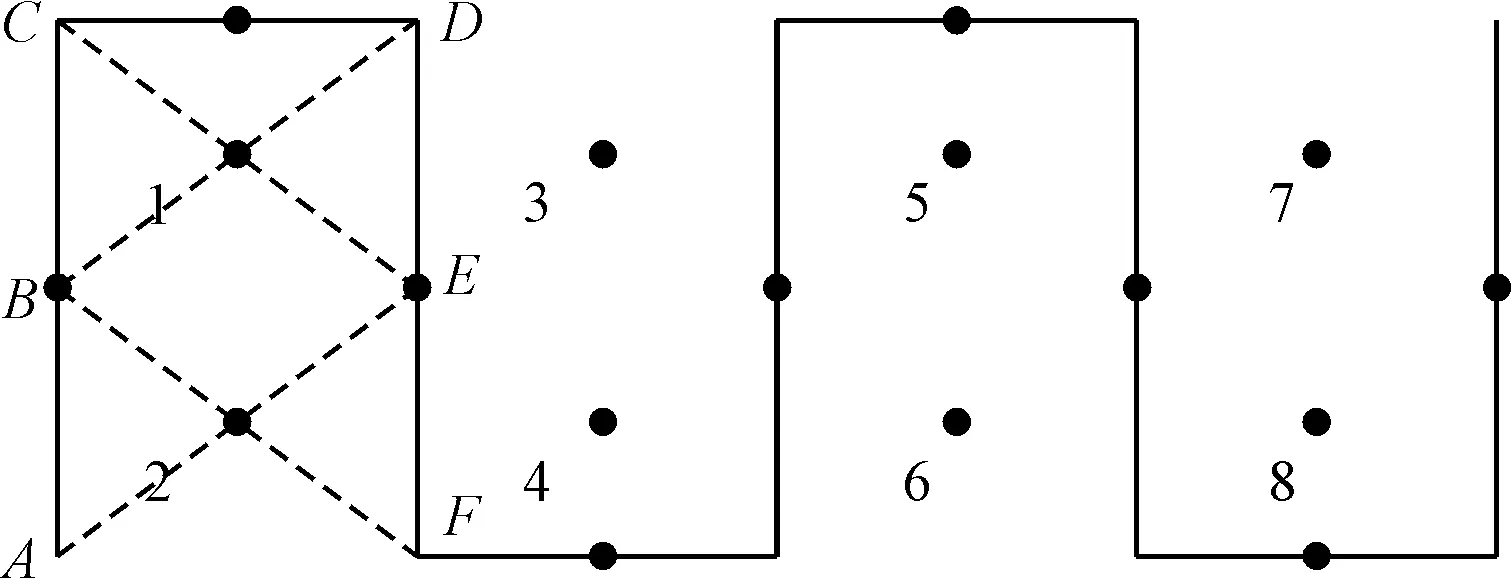
圖1　絕對測陣航路

圖1是絕對測陣所有潛標，船在GPS的引導下按預定航路航行，在A、B、C、D、E、F數據錄取點獲取所要潛標1和2的測距值及測量船相應位置GPS坐標數據。利用四點球面交匯可以定位潛標的位置。

2.2相對測陣

潛標具有自測陣功能。自測陣功能是指應答器可以由上級節點(測距儀或浮標)進行主從設置，采用“詢問-應答”的方式測量相鄰潛標之間的距離，這樣可以大大減少測陣的時間，可以快速地測出相對陣型[5～10]。

相對陣位坐標測量是指由于相鄰潛標彼此之間的距離是實測的(各潛標可測得)，因此，在已知潛標深度的情況下，某個潛標相對已知點的坐標，就可由兩個己知坐標的潛標及其彼此之間的距離測量值，通過求解兩個相交匯的圓方程，再結合已知的陣位投放初始位置確定其最終的陣位相對坐標。較為精確的圓交匯，是通過三個已知潛標坐標解算[6]。

3　航路設計

對海底陣的校陣可以采用絕對測陣和相對測陣相結合。絕對測陣，耗時長，但測量精度高；相對測陣，耗時短，精度較低。海底陣校陣可以先對某些潛標進行絕對測陣，得到大地坐標，這些點到相鄰潛標的距離可以通過潛標自測功能獲得，故而這些絕對測陣的潛標也可作為一個測量陣元。圖2航路設計，結合了絕對測陣和相對測陣的方法。

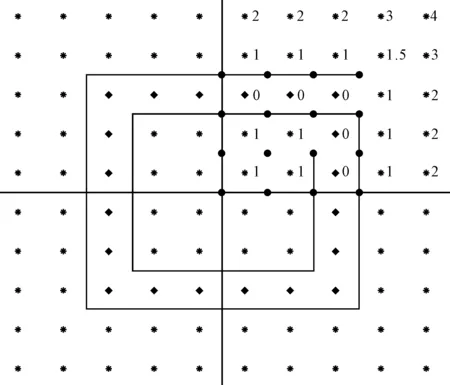
圖2　10×10潛標矩陣測量圖

圖2為10×10潛標構成矩陣，海底陣間距為2km，潛標間是通過電纜連接，并匯接到一個接駁盒中。圖中“回”型線表示航線軌跡，線上矩形點表示在航跡上選取的測量點。點表示通過絕對測陣的方式，利用四個測量點球面交匯的方式定位的潛標點[4]，用0表示。1處潛標的定位是通過試驗船測量點和已知潛標測距數據，1.5處潛標表示由試驗船測量點、1處已知潛標和0處已知潛標定位得到，2表示由1處已知潛標相對測陣得到，以此類推。數字大小也就反映了該位置處誤差傳遞的方向和精度。相對測陣的定位方式，在前面已經敘述，其可以通過兩個已知點或是兩點以上測量，航路二采用三個已知點定位的方式。

4　評估海底陣型測陣誤差的方法

4.1推算誤差

推算誤差，即計算上圖中標有數字處的潛標定位誤差。在0點處潛標存在的測量誤差為d0，即絕對測陣時的誤差，通過已知潛標測距未知潛標的誤差為d。通過相對測陣定位其他未知潛標，影響其定位誤差的因素有兩個方面，一是球面交匯誤差，二是已知潛標測距誤差。球面交匯造成的誤差，可以看成三個已知潛標點自身誤差的平均，總的誤差即為自身誤差的平均值加上它們測量未知潛標時的測距誤差。

分析航路二中標記數字點上的誤差，因為對稱的原因，只看右上角區域。假定d=k*d0，1處潛標的誤差長度為(1+k)*d0，2處潛標的誤差長度d+d1(d表示1處誤差長度)，3處潛標的誤差長度為d1+d*4/3，4處潛標的誤差長度為d1+d*17/9。1.5處潛標按1處潛標的誤差長度處理。

實際測量中，d0在良好水文條件下定位精度不大于5m，測距誤差d約為5m，故而它們的比值近似為1。測量1處潛標誤差長度時，還存在部分絕對測陣數據，將兩種數據取平均，可知1處誤差長度為7.5m。1～4標記點處的誤差依次為7.5、12.5、14.2、16.9m。

4.2誤差公式計算誤差

由多個點定位一個未知點，其解算方程式如下[2]：

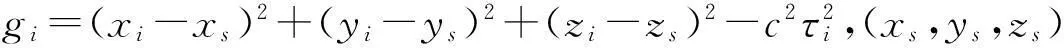
記x=f(x1，x2，x3，x4，y1，y2，y3，y4，z1，z2，z3，z4，c，τ1，τ2，τ3，τ4)

根據誤差傳遞理論可知[7～8]：

直接求上述誤差表達式比較復雜。若潛標的位置呈矩形排列，用距待測潛標最近的三個測量點進行定位解算。取三個測量點的坐標分別為：S1(0，0，0)，S2(0，L，h)，S3(L，L，h)，L為潛標間間隔，h為潛標深度。

將上述參數帶入方程，得：

三個方程式線性化得到：

容易解得：

求全微分得[9]：

公式中，dc取2m/s，dt=0.1ms，dL取決于該測量點自身的定位誤差長度。對于圖7中0點處潛標的誤差長度d0=5m，此時計算1處潛標誤差長度，dL=5m。故而可解算出1處潛標誤差長度為8m，2處潛標誤差長度為11.01m，3處潛標的誤差長度為13.9m，4處潛標的誤差長度為16.92m。

4.3建模仿真解算誤差

對航路二進行建模，以矩陣中心為坐標原點，仿真中只計算右上角區域。

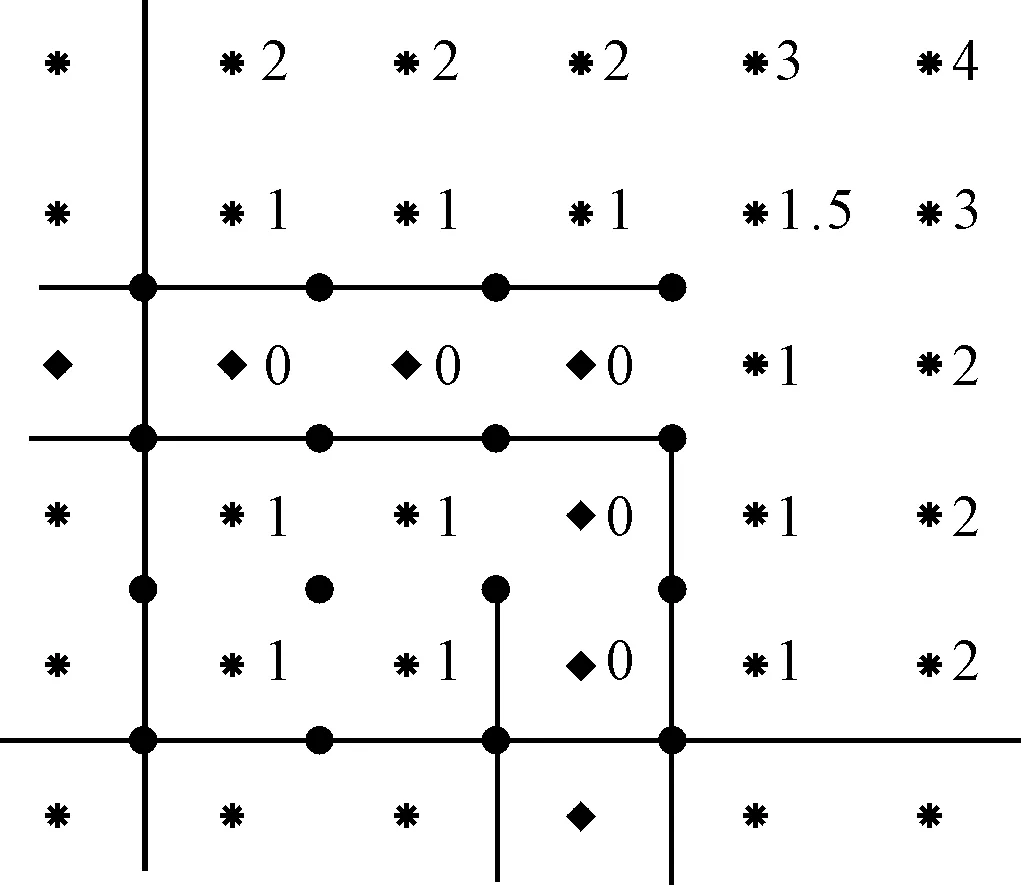
圖3　10×10陣型部分建模

坐標系中，已知點即圖中0處潛標點，其余都是要解算的點。設未知點的坐標為(x，y)，已知點為(x1，y1)，(x2，y2)，(x3，y3)，已知點到未知點的距離為k1、k2、k3則有：

(1)

(2)

(3)

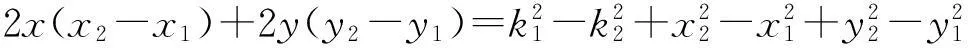
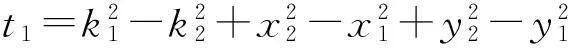
若已知點橫坐標互相不等，縱坐標互相不等，即三個已知潛標點不成直線則：

x=[t2-2y(y3-y2)]/[2(x3-x2)]

若已知三個潛標成直線，若與x軸垂直則

將y的值帶入式(1)，即可求得x值。同理可以解出與y軸垂直時的解。

仿真中，通過給已知潛標x、y方向上一個[0-5]隨機量表示。由已知潛標測量未知潛標的距離時，存在的誤差用[0-5]的隨機量表示。0處潛標誤差長度為5m。處理1處潛標誤差長度時，并未給予仿真計算，因為考慮到1處潛標的誤差長度還取決于船航行過程中的測量點測量的精度，故而1處潛標的誤差長度與前面推算誤差相同，誤差長度為7.5m。仿真計算2處潛標誤差長度為11.7m，3處潛標誤差長度為12.8m，4處潛標的誤差長度為15.75m。

5　結語

將上述三種計算潛標定位誤差方法的結果繪制成表1，并將其數據繪制成圖4。方法一，即推算誤差。方法二，即仿真建模解算誤差，將陣型建立坐標系，通過已知點坐標(包含誤差)利用公式計算其他位置潛標各點。方法三，即誤差公式求解誤差。

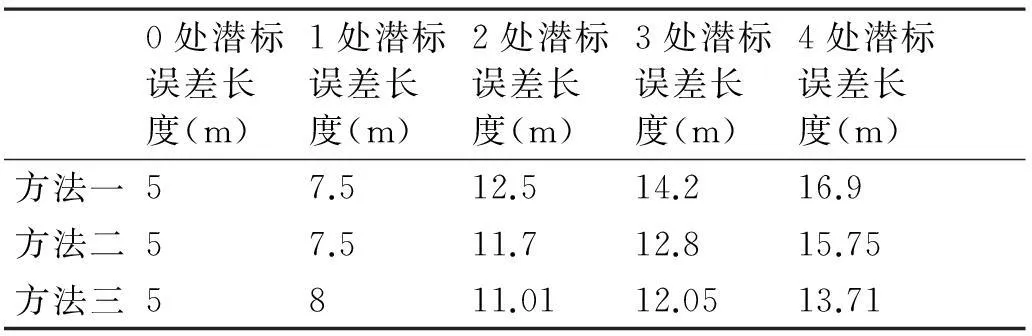
表1　三種方法誤差長度對比

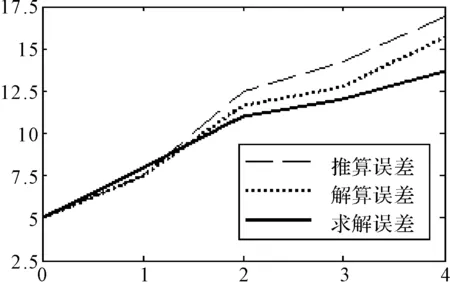
圖4　三種方法誤差長度變化趨勢

由表1數據和圖4可知，三種方法反映誤差傳遞過程中的誤差變化規律是一樣的。方法一直觀、計算快捷；方法二建模仿真過程復雜，結果可靠性好，方法三基于理論計算，計算的誤差較前兩者小。

在優選海底陣型校陣航路中，選用的優選方式只需近似反映定位誤差的變化情況，而在排選效率上要求高，可以采用方法一(推算誤差)計算每種航行路線在校陣中各陣元點誤差值，并求出平均誤差，用推算的結果評判設計的多種航行路線的優劣。

參 考 文 獻

[1] 孫大軍，鄭翠娥，錢洪寶,等.水聲定位系統在海洋工程中的應用[J].聲學技術，2012，31(2)：8-9.

[2] 李莉.長基線陣測陣校陣技術研究[D].哈爾濱：哈爾濱工程大學，2007:30-33.

[3] 張宏偉，林芳.基于長基線系統絕對測陣的測距修正算法優化[J].大慶師范學院學報，2014，3(3)：1-3.

[4] 劉百峰，楊志權,等.一種適用長基線系統絕對測陣的新航路[J].艦船電子工程，2011，31(6)：172-174.

[5] 王先華.長基線水下導航定位系統測陣校陣及系統集成[J].工程勘察，2010，8：49-53.

[6] 田春和，秦建.基于長基線水聲定位系統水下定位技術初步應用研究[J].水道港口，2015，3：268-271.

[7] 高國青，葉湘濱，喬純捷,等.水下聲定位系統原理與誤差分析[J].四川兵工學報，2010，6(6)：95-97.

[8] 于運治，姜璐，郭志強.一種水下精確定位方法及其誤差分析[J].四川兵工學報，2012，32(9)：121-123.

[9] 徐躍良,等.數值分析[M].成都：西南交通大學出版社，2015:80-88.

[10] 劉焱雄，彭琳，吳永亭,等.超短基線水聲定位系統校準方法研究[J].武漢大學學報，2006，7(7)：610-612.

*收稿日期：2015年10月21日,修回日期：2015年11月30日

作者簡介：張永超，男，碩士，助理工程師，研究方向：電磁場與微波技術。徐國貴，男，碩士，工程師，研究方向：水聲通信。

中圖分類號TB565

DOI：10.3969/j.issn.1672-9730.2016.04.034

Evaluation Methods on Array Measuring Error of Seabed Arrays

ZHANG YongchaoXU Guogui

(No. 91388 Troops of PLA, Zhanjiang524022)

AbstractThe measuring theory for seabed acoustic arrays is divided into absolute array measuring and relative array measuring. Absolute array measuring takes much time， but it has high precision of array measuring. Relative array measuring is in contrast to absolute array measuring. Comparering with the two measuring method， three methods of array measuring error in evaluating seabed acoustic arrays are given， which can help us find a better sailing path. The method one is prediction error， which marks the error’s direction and size as a point in a picture and estimates the error of the point as array measuring error. The method two is making use of modeling and simulation and calculating the array measuring error. The method three is calculating error by use of the error equation. Comparing the three methods， it is concluded that the three methods are of consistency on the change rule in the error trasfering， and the method one has advantages of graphics intuition and calculating fast， and the method two is reliable.

Key Wordsseabed arrays, array measuring and calibration, array measuring error, evaluation methods