以高中數學為例，談學生思維能力的培養

蔡寶祥（鹽城市東臺市三倉中學）

以高中數學為例，談學生思維能力的培養

蔡寶祥
（鹽城市東臺市三倉中學）

思維能力是指通過一系列的分析、綜合與概括，將感性的材料進行加工整理并轉化為理性認識以及解決問題的一種能力。看一個人是否聰明、有沒有智慧，主要就看他的思維能力強不強。

高中數學；思維能力；邏輯思維

高中階段學習的重點及難點學科之一是高中數學。而培養思維能力是學好數學最根本，也是最有效的辦法。下面我就簡單分享一下我在教學中的經驗。

一、推陳出新，培養獨創思維

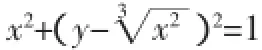
二、聚合抽象，培養創造性思維

聚合抽象指的就是將相似的事物按照一定的標準進行分類，以便歸納事物的共性與本質特點。要想運用好這種方法，就要做到以下三點。首先，要對相似的事物形成總體的認識，從感覺上找出其突出的特點；然后，從共性到個性，對問題進行肢解分析，抽象出事物的本質特征；最后，對抽象出的事物本質進行描述，形成具有指導意義的理論成果。

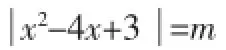
三、循序漸進，培養邏輯思維

學習本身就是一個循序漸進的過程，在做高中數學題時，更不能一味地為了做題而做題。很多高中學生，迫于現在考試的壓力，為了追求高分數，只注重“題海戰術”，認為題做得多了，成績自然就能上去。這種做法在短時間內雖然會起到顯著的作用，但是從長遠來看，學生很容易因為疲勞而對數學學習失去興趣與信心。高中數學的主要作用就是培養學生分析問題、解決問題的邏輯思維能力，只顧做題而不加思考，不注重邏輯思維能力的培養，很難學好高中數學。

在立體幾何的學習中，我發現班里有很多學生在解題時不知從何處入手，即使是簡單的證明題思路也不清晰，沒有條理性。后來我在上課時，就著重培養學生的邏輯推理、逆向思維能力。

例，在正方體ABCD-A1B1C1D1中，O是底面ABCD的中心，M、N分別是棱DD1、D1C1的中點，求證直線OM是AC和MN的公垂線。

分析：要證明OM是AC和MN的公垂線，即要證明OM⊥AC，OM⊥MN。那么作OM在面ABCD上的射影，即連接OD，那么根據三垂線定理，則能證明OM⊥AC，同理可證OM⊥MN。

經過一段時間，學生的邏輯分析能力和解題能力都有了顯著的提高，同時課堂的教學質量也得到了有效的保證。因此，我覺得我們在教學過程中，不能只注重學生的學習成績，更要注重對他們邏輯推理能力的培養，讓他們能夠運用邏輯思維能力分析并處理生活中遇到的各種問題。

四、生疑提問，培養創新思維

生疑提問是指對過去或現在一直被人們認為正確的東西或某種固定的思考模式提出質疑，敢于并善于提出自己的觀點和建議，并且能夠運用各種理論和證據來證明結論的正確性。要做到生疑提問，就要明確以下兩點：首先，每當觀察到一件事物或現象時，無論是初次還是多次接觸，都要養成問“為什么”的習慣，不要害怕丟臉，覺得沒面子；其次，每當我們遇到困難時，都應盡可能地從不同角度、不同方向觀察、分析問題，以免被固有的思維模式困住。

總而言之，在高中數學教學中，我們不僅要傳授給學生知識，還要注重對他們各種思維能力的培養與提高。思維能力是學習能力的核心，只有培養并提高學生的思維能力，使學生得到全面的發展，才能成為適應社會需要的復合型人才，成為國家的棟梁之才。

白慧明.高中數學教學中培養數學思維能力的實踐研究［D］.信陽師范學院，2015.

·編輯 薄躍華