聯合VLBI和天文導航的月球車定位結果分析
魏二虎 湯深權 金雙根 劉經南
1 武漢大學測繪學院,武漢市珞喻路129號,430079 2 中國科學院上海天文臺,上海市南丹路80號,200030 3 武漢大學GNSS研究中心,武漢市珞喻路129號,430079
?
聯合VLBI和天文導航的月球車定位結果分析
魏二虎1湯深權1金雙根2劉經南3
1武漢大學測繪學院,武漢市珞喻路129號,4300792中國科學院上海天文臺,上海市南丹路80號,2000303武漢大學GNSS研究中心,武漢市珞喻路129號,430079
摘要:推導了聯合甚長基線干涉測量(VLBI)和天文導航的月球車定位計算公式,并利用嫦娥三號(CE-3)實測數據分別解算VLBI單獨定位和聯合天文導航定位的月球車定位結果。結果表明,聯合定位相對于單獨VLBI定位,提高了天文導航的定位精度,改善了月球車的定位精度;同時,聯合VLBI和天文導航定位也保障了月球車定位的可靠性與穩定性。
關鍵詞:VLBI; 天文導航; 聯合定位; 深空探測; 月球車
月球車要提高自身生存能力以及順利開展科學探測任務,關鍵是獲取自身的位置信息[1]。對于月球車定位方法,國內外學者提出了同波束VLBI定位、天文導航、慣性導航(包括航位推算)、視覺導航等方法[2-3]。甚長基線干涉測量(VLBI)技術具備高精度、高分辨率等特點,在我國“嫦娥工程”的月球探測器實時精密定軌、定位中發揮了重要作用[4]。天文導航具有穩定性高、自主性強等特點,廣泛應用于船體、衛星及軍事武器設備的導航中[5]。VLBI定位技術可以提供高精度的位置信息,但由于受一些外部因素的影響,VLBI信號可能無法接收,導致其不能正常工作,月球車定位的穩定性和可靠性會因此受到影響。天文導航方法不受時間、距離長短的影響,能夠提供姿態和位置信息,但其短時定位精度較VLBI低。本文提出聯合VLBI和天文導航的月球車定位方法并推導了聯合定位公式,對今后天文導航用于月球車定位,提高月球車定位的穩定性和可靠性具有實際意義。
1 嫦娥三號(CE-3)月球車定位模型
1.1VLBI定位模型
A、B表示地面上2個VLBI測站點。設月球車信號到達A、B測站的時間分別為t1、t2,月球車與測站之間的距離分別為r1、r2,則:
(1)
式中,c表示光速,τ12表示信號到達測站A、B的時間差,(x1,y1,z1)為測站A的坐標,(x2,y2,z2)為測站B的坐標,(xs,ys,zs)為月球車的坐標。對式(1)進行線性化,按泰勒級數展開,舍去二次冪以上項,可得誤差方程:
cτo-c+a11dxs+a12dys+a13dzs=
a11dxs+a12dys+a13dzs
(2)
式中,dxs、dys、dzs為月球車坐標改正數,τo為時延觀測值,τc為理論幾何時延值,τo-c為時延觀測值與理論值之間的差值,(xs0,ys0,zs0)為t0時刻月球車的坐標初始值。 目前,中國有4個VLBI測控站,可以組成6條觀測基線,建立如下誤差方程:
(3)
僅使用VLBI得到的時延信息來轉換成角位置信息時,會有較大的誤差。因此,在實際解算月球車位置時,往往需要加入月球車的距離約束條件。可建立如下月球車距離條件限制方程:
(4)
對式(4)進行線性化并代入初始值,得:
(5)
聯合式(3)和式(5),得到VLBI解算的誤差模型:
(6)
1.2天文導航定位模型
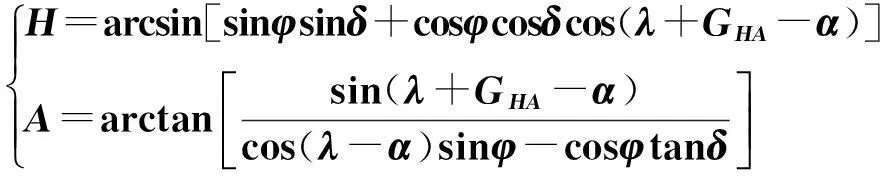
(7)
式中,H、A分別是目標天體在月球車所在水平坐標系中的高度角和方位角,α、δ分別為目標天體的赤經、赤緯,GHA為春分點的格林尼治時角。為方便計算,本文將sinH、tanA當作“虛擬觀測值”,并對上述觀測方程進行線性化,得:
(8)
式中,(sinH)0、(tanA)0是觀測值的近似值;其他系數如下:
(9)
式中,LHA為目標天體的地方時角。本文選取太陽和地球為目標觀測星體,其中HE、AE表示地球對應的高度角和方位角,HS、AS表示太陽對應的高度角和方位角。可以建立如下誤差方程:
(10)
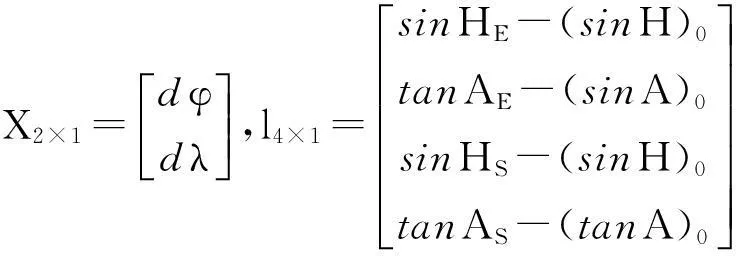
觀測值模擬的具體流程如下:
1)通過JPL星歷(本文采用DE423)獲取目標天體相對于月球的三維坐標,通過坐標轉換,轉換成觀測星體的赤緯、赤經;
2)將通過VLBI解算的月球車月固直角坐標通過坐標轉換,轉換成月固系下的赤經、赤緯;
3)將步驟1)、2)得到的值代入式(8),模擬出天文導航的觀測值;
4)加入觀測誤差,如星敏感器誤差、星歷誤差等。
1.3聯合定位模型
采用兩種系統進行月球車定位,可以增強系統的穩定性,并使其容錯性得到提升。由于月心直角坐標和月心大地坐標存在如下函數關系:
(11)
式中,N表示卯酉圈半徑:
a為橢球長半軸,e為橢球第一離心率。由于月球車活動范圍地勢較為平坦,故本文假設月面高程不變,采用固定值-2.64 km(由NASA、LRO圖像處理得到),求解月球車的月固坐標(xs,ys,zs)及(λ,φ)。先對式(11)求全微分,設B2矩陣為:
B2=
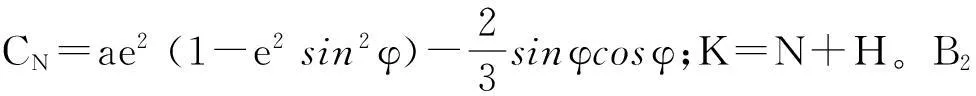
(12)
將式(12)代入式(6),對應的誤差方程為:
(13)
則可得VLBI聯合天文導航的誤差方程:
(14)
設VLBI和CNS解算時的權矩陣分別為PVLBI、PCNS。由于給定的初始權矩陣不合理,故本文采用赫爾默特方差估計法進行隨機模型的驗后估計[6]。先給定各類觀測值的初始權值,再進行迭代平差,直到各類單位權方差之比等于1為止。然后,迭代解算得到PVLBI、PCNS。最后采用最小二乘法解算出參數λ、φ,代入式(11),得到月球車的月固坐標。
2 實例解算分析
本文以嫦娥三號(CE-3)實測數據為例,采用北京(BJ)、昆明(KM)、烏魯木齊(UR)和上海(TM)4個測站2013-12-20 19:41:57.439 125~20:48:32.439 156的觀測數據,來進行月球車位置的解算,并模擬天文導航觀測值。在模擬天文導航觀測值的過程中,分別取太陽敏感器測量精度為6″,地球敏感器測量精度為36″,采樣間隔為5s(同VLBI采樣間隔一致)[7-9],得到的“虛擬觀測值”殘差如圖1(EA表示高度角,AZ表示方位角)。
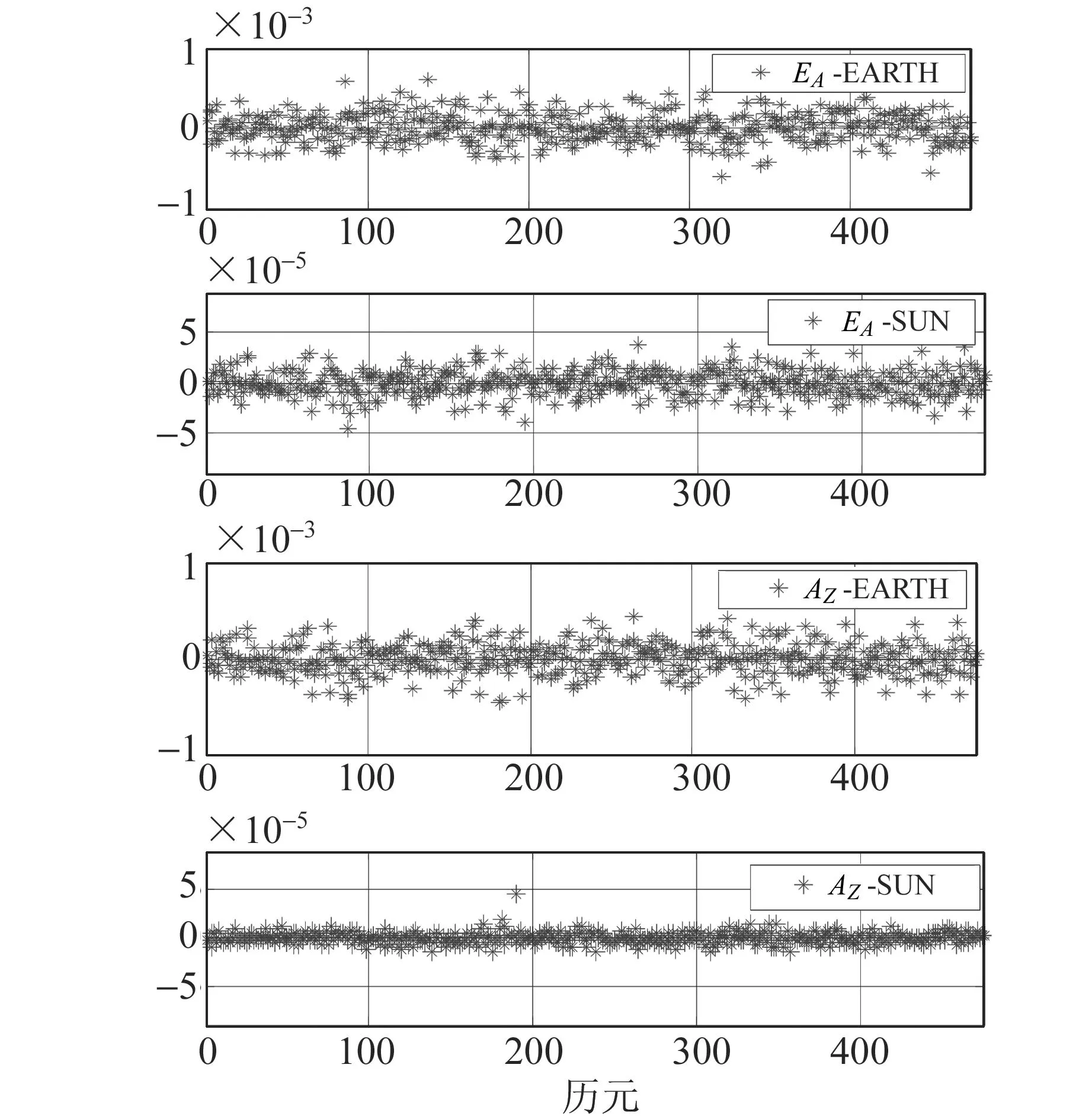
圖1 天文導航解算的觀測值殘差Fig.1 Plots of observation residuals calculated by celestial navigation
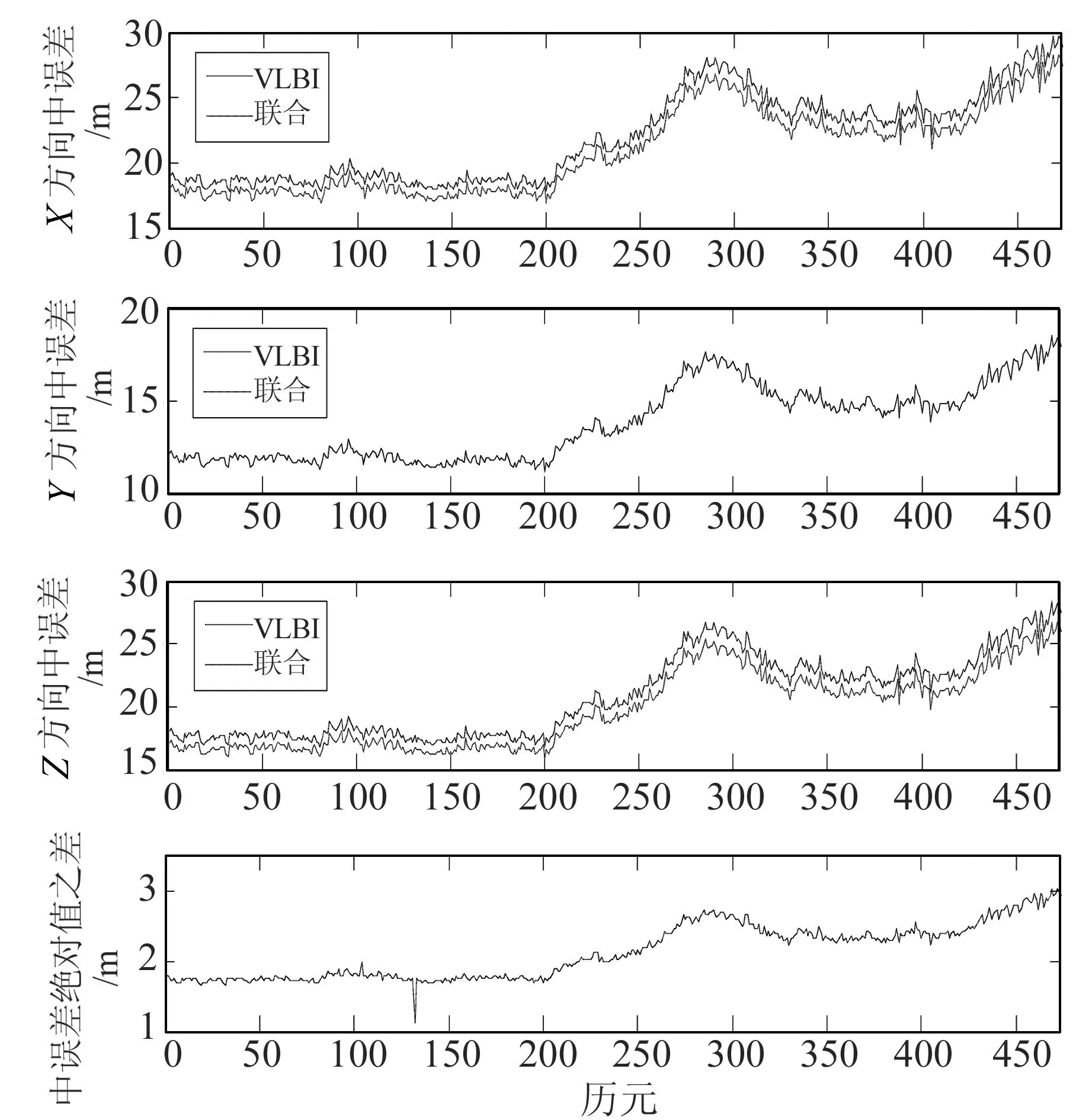
圖2 聯合解算和VLBI單獨解算的對比Fig.2 Comparison of joint solution and single solution of VLBI
由圖1可知,所有觀測值的殘差值接近于0,并且沒有出現系統性誤差,呈白噪聲分布趨勢,說明仿真過程成功解算了參數值。同時可以看出,地球敏感器的加入誤差比太陽敏感器要大,這是由于太陽的光源極強、視場很大,太陽敏感器的分辨率可達到角秒級;而地球敏感器工作波段一般選在14~16 μm的二氧化碳紅外窄波段上,收斂速度較慢且對初始誤差非常敏感,導致地球敏感器的測量精度相對較差[7-9]。
月球車定位實際是一個不斷迭代求解的過程。通過誤差方程求解獲得改正數,再將初值和改正數之和作為待求參數,進一步構造誤差方程進行解算,直到小于一定的闊值時解算得到最終值。圖2表示分別采用VLBI技術和聯合定位時,月球車X、Y、Z3個方向的坐標中誤差,最下面的圖表示兩者的三維坐標中誤差絕對值之和的差值。
可以看出,聯合解算較VLBI單獨解算在X方向、Z方向的精度有一定程度的提高,Y方向變化不明顯。X方向精度提高的最大值為2.0 m,最小值為0.60 m,平均值為1.02 m;Z方向精度提高的最大值為2.14 m,最小值為0.67 m,平均值為1.10 m;Y方向提升的最大值為0.07 m。這是因為,觀測信號的投影大都集中在Y方向,Y方向反映了較真實的觀測精度[10],故聯合解算較VLBI單獨解算改善較小。三維坐標中誤差絕對值之和的差值,最大為4.14 m,最小為1.11 m。這說明,聯合解算較VLBI單獨解算提高了月球車定位的精度。圖3表示的是聯合解算和VLBI解算分別求得的X、Y、Z參數的差值DX、DY、DZ。
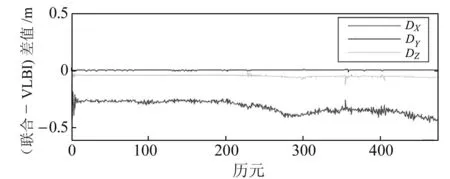
圖3 參數解算的差值Fig.3 Difference of parameters calculation
由圖3可以看出,聯合解算和VLBI單獨解算得到的月球車月固坐標的差值很小,Y方向和Z方向幾乎為0,X方向也都小于0.5 m。這說明,聯合VLBI和天文導航進行月球車月固坐標參數求解的過程是正確的。
圖4、圖5分別表示天文導航單獨解算和聯合解算時經緯度方向的誤差(模擬值和解算值之間的差值)。可以看出,由于天文導航短時精度受測量儀器精度的限制,導致其精度較低,在單獨采用天文導航進行解算時,經緯度方向的誤差較大并且波動也較大。而采用聯合解算時,因為加入了VLBI觀測量和距離限制條件,使得經緯度方向的誤差波動小了很多。緯度方向誤差范圍在-31~-33 m,經度方向誤差范圍在5.5~6.5 m。在加入VLBI觀測量之后,天文導航的解算更加穩定且解算精度有較大提升。
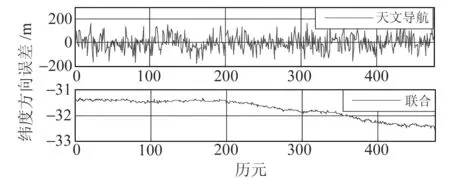
圖4 緯度方向誤差對比Fig.4 Comparison of error in latitudinal direction
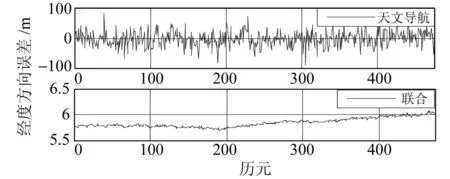
圖5 經度方向誤差對比Fig.5 Comparison of error in longitude direction
3 結 語
本文分別介紹并推導了月球車VLBI定位模型、天文導航定位模型以及VLBI聯合天文導航定位模型。模擬了天文導航觀測量,并以嫦娥三號(CE-3)實測數據進行解算。
1)在加入天文導航后,聯合解算較VLBI單獨解算在X、Z方向的坐標誤差有所減小,月球車定位的精度得以提升。
2)在加入VLBI觀測量之后,天文導航的解算變得更加穩定,精度也得到較大提升。
該聯合定位模型也存在不足,例如VLBI定位方式的主要優勢是角向精度較高,缺陷是視向精度較差。就星敏感器的工作原理而言,也是角度敏感的觀測方式。如果將VLBI數據和測距、測速數據結合,則角向、視向精度會更高,二者結合會有更好的互補性。
參考文獻
[1]寧曉琳,房建成. 一種基于天體觀測的月球車位置姿態確定方法[J]. 北京航空航天大學學報,2006,32(7):756-757(Ning Xiaolin, Fang Jiancheng. Position and Pose Estimation by Celestial Observation for Lunar Rovers [J]. Journal of Beijing University of Aeronautics and Astronautics, 2006,32(7):756-757)
[2]喬書波,李金嶺,孫付平. VLBI在探月衛星定位中的應用分析[J]. 測繪學報,2007, 36(3):262-268(Qiao Shubo, Li Jinling, Sun Fuping. Application Analysis of Lunar Exploration Satellite Positioning by VLBI Technique[J].Acta Geodaetica et Cartographica Sinica, 2007, 36(3):262-268)
[3]Moore M, Wang J. An Extended Dynamic Model for Kinematic Positioning[J]. The Journal of Navigation, 2003,56(1): 79-88
[4]李征航,魏二虎,王正濤,等. 空間大地測量學[M]. 武漢: 武漢大學出版社,2010(Li Zhenghang, Wei Erhu, Wang Zhengtao,et al. Space Geodesy[M]. Wuhan: Wuhan University Press, 2010)
[5]Benjamin P M. Celestial Navigation on the Surface of Mars[R]. ADA392455,2001
[6]崔希璋,於宗儔,陶本藻,等. 廣義測量平差[M]. 武漢:武漢大學出版社,2009(Cui Xizhang, Yu Zongchou, Tao Benzao, et al. Generalized Surveying Adjustment[M]. Wuhan: Wuhan University Press, 2009)
[7]岳富占,崔平遠. 基于地球敏感器和加速度計的月球車自主定向算法研究[J]. 宇航學報,2005,26(5):553-557(Yue Fuzhan, Cui Pingyuan. Earth Sensor and Accelerometer Based Autonomous Heading Detection Algorithm Research of Lunar Rover[J]. Journal of Astronautics, 2005, 26(5):553-557)
[8]張萬永. 高精度太陽敏感器原理與精度穩定性分析[J].光電技術應用,2009,24(6):32-33(Zhang Wanyong. Analysis of Principle and Accuracy Reliability of High Accurate Sun Sensor[J]. Electrooptic Technology Application, 2009, 24(6):32-33)
[9]吳江. 月球探測器多源天文自主導航方法研究[D]. 哈爾濱:哈爾濱工業大學,2013(Wu Jiang. Study on Multi-source Celestial Autonomous Navigation of Lunar Probe [D]. Harbin: Harbin Institute of Technology, 2013)
[10] Wei E H, Jin S G, Yang H Z, et al. Simulation and Results on Real-Time Positioning of Chang’e-3 Rover with the Same-Beam VLBI Observations[J]. Planetary and Space Science,2013,84: 20-27
Foundation support:National Natural Science Foundation of China,No.41374012.
About the first author:WEI Erhu, professor, PhD supervisor, majors in space geodesy and geodynamics, E-mail: ehwei@sgg.whu.edu.cn.
收稿日期:2015-09-08
第一作者簡介:魏二虎,教授,博士生導師,主要從事空間大地測量和地球動力學研究,E-mail: ehwei@sgg.whu.edu.cn。
DOI:10.14075/j.jgg.2016.08.011
文章編號:1671-5942(2016)08-0703-05
中圖分類號:P228
文獻標識碼:A
Positioning Results of Lunar Rover Based on Combined VLBI and Celestial Navigation
WEIErhu1TANGShenquan1JINShuanggen2LIUJingnan3
1School of Geodesy and Geomatics,Wuhan University,129 Luoyu Road, Wuhan 430079,China2Shanghai Astronomical Observatory, CAS,80 Nandan Road, Shanghai 200030,China3GNSS Research Center,Wuhan University,129 Luoyu Road, Wuhan 430079,China
Abstract:The calculation formula of lunar rover positioning based on VLBI and celestial navigation is presented in the paper. The results of VLBI positioning and joint positioning based on combined VLBI and celestial navigation are calculated with the measurement data of Chang’e-3 (CE-3). This shows that joint positioning can improve the positioning accuracy of lunar rover by celestial navigation or VLBI alone. Furthermore, joint positioning can also guarantee the reliability and stability of lunar rover positioning.
Key words:VLBI;celestial navigation;joint positioning;deep space exploration;lunar rover
項目來源:國家自然科學基金(41374012)。

