最小二乘法的幾點研究
云南省會澤縣待補中學 浦 帥 王利娟
?
最小二乘法的幾點研究
云南省會澤縣待補中學浦帥王利娟
最小二乘法是科學實驗和統計工作中常用的一種數據處理方法,解決如何從一組測量值中尋求規律,其基本原理是:成對等精度測得一組數據 ,找出一條最佳的擬合曲線,使這條擬合曲線上的各點的值與測量值的差的平方和在所有擬合曲線中最小,即從一組實驗數據(xi,yi)(i=1,2,…,n)中尋找自變量x與因變量y之間的函數關系y=f(x)。由于觀測數據不準確,因此不要求y=f(x)經過所有數據點,只要求所在所有給定點xi上的偏差的平方和達到最小。
最小二乘法 歷史發展 數據擬合 多項式
一、引言
十八世紀,最小二乘法就由高斯首先創立,成功地應用于天文觀測和大地測量工作中。三百年來,它已廣泛應用于科學實驗與工程技術。隨著現代電子計算機的普及與發展,這個古老的方法顯示出強大的生命力。
無論是經濟管理、社會科學、醫學還是工程技術、工業實驗往往會遇到這樣的情況:實驗產生n組數據(xi,yi)(i=1,2,…,n),其中橫坐標xi是明確的,而最小二乘法的目標之一,根據使誤差的平方和最小的原則確定一個函數y=f(x),將這些變量聯系起來,從一類允許的函數中進行選擇并最終確定它們的系數。選擇函數的可能性是多樣的,本文從線性函數和非線性函數以及多項式函數三種形式,給出函數y=f(x)的確定方法。
二、最小二乘法的基本原理和多項式擬合
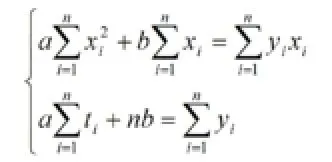
三、最小二乘法的矩陣原理
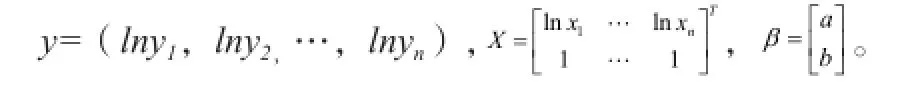
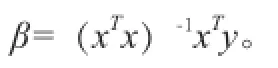
四、多項式擬合
定義4 給定數據(xi,yi)(i=1,2,…,n),在取定的函數類Φ中,求P(x)∈Φ,使誤差,1,…,n )的平方和最小,即,從幾何意義上講就是尋求與給定點的距離平方和為最小的曲線y=P(x)。這樣就把函數P(x)稱為擬合函數或最小二乘解,求擬合函數P(x)的方法稱為曲線擬合的最小二乘法。
五、一般最小二乘擬合
多項式擬合形式比較規范,方法也比較簡單,但在實際應用中,針對所討論問題的特點,擬合函數可能為其他類型,如指數函數、有理函數、三角函數等,這就是一般最小二乘擬合問題。
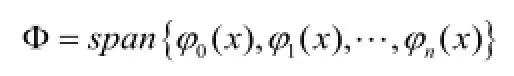
六、總結
本文通過對最小二乘法的幾點研究全面介紹最小二乘法及其一些應用,對于解決實際社會生產生活中的數據問題有著重要的作用。今后的學習和研究中我們將不斷深入探討,結合線性模型及正規方程的計算理論對數據進行研究,發現其中的規律與問題,以彌補本文不足。
[1]賈小勇,徐傳勝,白 欣.最小二乘法的創立及思想方法[J].西北大學學報,2006
[2]徐傳勝,呂建榮.亞伯拉罕·莫夫的概率思想與正態概率曲線[J].西北大學學報,2006
ISSN2095-6711/Z01-2016-06-0182

