基于分數階 PIλDμ的船舶航向控制

張安明，孫　潔，黃　晶，劉　健（. 海軍駐大連46廠軍事代表室，遼寧 大連 6000；. 東部戰區海軍裝備部信息系統處，浙江 舟山6000；. 中國船舶重工集團公司第七〇七研究所 九江分部，江西 九江 007）

基于分數階 PIλDμ的船舶航向控制

張安明1，孫潔2，黃晶3，劉健3
（1. 海軍駐大連426廠軍事代表室，遼寧 大連 116000；2. 東部戰區海軍裝備部信息系統處，浙江 舟山316000；3. 中國船舶重工集團公司第七〇七研究所 九江分部，江西 九江 332007）

船舶在海上航行時受到海風、海浪和海流等環境擾動作用，這造成在不同航速下船舶動力學模型的參數不確定性，本文對船舶本體運動和風浪流干擾進行建模，提出一種基于分數階 PIλDμ的抑制風浪干擾的的航向控制算法，并與傳統 PID 算法進行對比，針對某型船舶動力學模型在 6 級海風和 5 級海浪海況下進行對比數字仿真。仿真結果表明，該算法在不同航速下具有較好的控制品質和魯棒性，對風浪干擾具有良好的適應性，可應用于船舶的航向控制，易于工程實現。

船舶控制；航向控制；分數階 PIλDμ

0　引　言

非線性與不確定性是船舶運動的重要特征，船舶在海上航行時受到海風、海浪和海流等海洋環境擾動作用，風浪流的作用存在強非線性和強不確定性，這造成航向會出現不可避免的不斷改變［1］。船舶在以不同航速進行航行的過程中，受到海風、海浪和海流的作用效果大小很不一致，操縱機構舵機在不同航速情況下的舵面效率也不一致，低航速下舵效低而高航速下舵效高，這造成在不同航速下對船舶進行建模過程中的模型參數的不確定性，這些因素都會對實現船舶高精度和高穩定度的航向控制帶來嚴重的困難。

經典PID控制及相關改進方法應用最為廣泛，廣泛應用于航空、航天、航海［2］和化工等各種工業控制中。在經典的 PID 控制中，Ki， Kp和 Kd分別為系統過去、現在和將來的誤差信息比例，控制器綜合系統的過去、現在和將來的誤差信息傳遞給操縱結構進行調整，控制器需要的傳感器信息量較少，控制器結構簡單并易于實現。隨著分數階微積分學理論的發展，國內外學者對分數階 PIλDμ控制方法進行廣泛研究［6-11］，國外 Dorcak L.［7］和 Podlubony I.［8］提出 MFOPID（Fractional Order Proportion Integration Differentiation，FOPID）控制器，國內曾慶山［9］對分數階 PIλDμ控制器進行比較系統的仿真研究，應用在 W 平面上的根軌跡分析控制參數對系統的影響，金永順［11］針對不同控制對象的提出MFOPID 控制器參數魯棒性的整定方法。分數階 PIλDμ控制器的階次可以為任意實數，這種控制器結構更為精細，對系統過去、現在和將來的誤差信息綜合也更完整，控制效果穩定而不易發散，調節控制更為細膩，系統動態性能更良好，逐漸受到控制領域國內外學者重視。

1　船舶運動模型

船舶首搖響應的線性方程式為：

在操舵不是很頻繁的情況下，船舶的運動可以看做一個大質量物體在舵作用下的緩慢轉首運動，因此可以對船舶運動方程進行簡化，野本謙作［1， 4］提出可用以下傳遞函數簡化

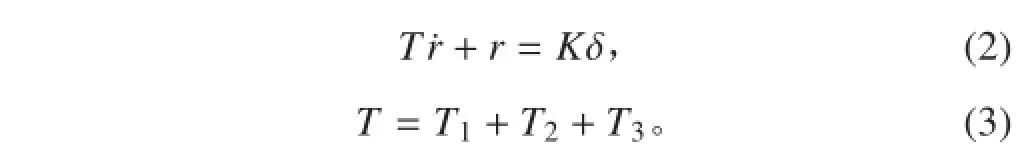
上式稱為一階 KT 方程，其中 K 稱為回轉性參數，T 為穩定性參數。

某型船舶首搖運動的數學模型，在航行速度 15 kn 和 24 kn 下開環 Bode 圖如圖1 和圖2 所示。舵液壓執行機構模型簡化方框圖如圖3 所示。

圖1　航速 15 kn 下艏搖運動的 Bode 圖Fig. 1　The yawing Bode diagram for velocity of 15 knots

舵液壓執行機構的運動模型可簡化為一階慣性環節［3］形式，即

圖2　航速 24 kn 下艏搖運動的 Bode 圖Fig. 2　The yawing Bode diagram for velocity of 24 knots

船舶因為受到海風、海浪和海流的干擾作用而產生偏移。海風產生的首搖干擾力矩［9］為

海浪產生的首搖干擾力矩為：

式中：k1為波數；為第 i 個諧波波面偏離靜水面的高度；L 為船長；Bm為船寬；和分別為諧波的初相角和船舶的遭遇頻率。

記

海流產生的首搖干擾力矩為

2　分數階 PID 控制器設計方法

定義連續的分數階微積分算子如下［8］：

意大利數學家 M. Caputo［11］為調和分數階微積分在數學和物理應用上的矛盾，提出新的分數階微積分定義如下：

從 Caputo 分數階微分定義，可以得到其任意正數階 Laplace 變換，可表示為：

類比于整數階 PID 控制器，用微分方程表示分數階 PID 控制器如下：

進行拉氏變換得到分數階 PID 控制器的傳遞函數為：

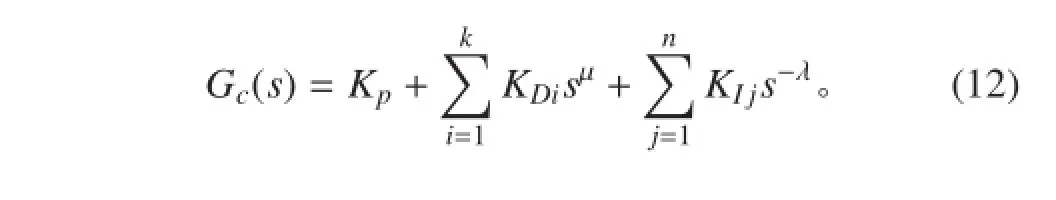
3　分數階 PID 控制器設計

通過 Symbolic Math Toolbox 控制箱進行選擇分數階控制系統參數設計，得到控制系統 Bode 圖如圖4和圖5所示。

如圖4 所示，在航速 15 kn 時，航向保持回路為穩定回路，截止頻率為 0.109 rad/s，相角裕度為 76.1°；如圖5 所示，在航速 24 kn 時，航向保持系統為穩定回路，截止頻率為 0.177 rad/s，相角裕度為 87.5°，相角裕度滿足一般控制系統指標要求［12］。

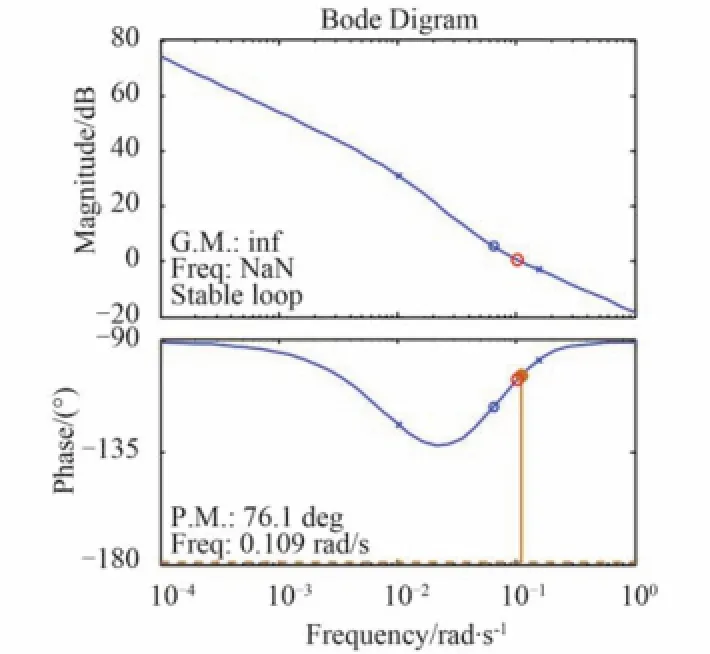
圖4　航速 15 kn 下閉環系統 Bode 圖Fig. 4　The Bode diagram of closed loop system for velocity of 15 knots

圖5　航速 24 kn 下艏搖運動的 Bode 圖Fig. 5　The Bode diagram of closed loop system for velocity of 24 knots

4　仿真試驗與數據分析

將設計好的分數階 PIλDμ控制器參數和整數階 PID控制器分別對船舶非線性模型進行數字仿真，仿真中加入 6 級海風和 5 級海浪干擾擾動，為驗證所設計分數階控制器的魯棒性和適應性，分別對船舶航速在 15 kn 和 24 kn 下進行仿真。

針對 6 級海風和 5 級海浪風浪干擾下某型船舶的非線性動力學模型，航速分別為低航速 15 kn 和高航速 24 kn 下進行數字仿真，仿真結果如圖6 ～ 圖9 所示。船舶在低航速 15 kn 情況下，從 MFOPID 控制和PID 控制仿真結果看出，MFOPID 控制器下系統具有較短的調節時間和超調量，且打舵次數且打舵量的平均幅度與采用傳統 PID 控制器的系統基本相當；在高航速 24 kn 下，采用 MFOPID 控制器與傳統 PID 控制器相比則具優越性，采用 MFOPID 控制器，閉環系統具有更小的超調和更短的調節時間，且打舵次數與打舵量的平均幅度與采用傳統 PID 控制器的系統基本相當。試驗結果表明，采用 MFOPID 控制器系統，船舶在面對風浪干擾和模型攝動時也能具備比較好的航向穩定性。

圖6　航速 15 kn 下航向保持回路仿真響應曲線圖Fig. 6　The simulating response curves of heading-hold loop for velocity of 15 knots

圖8　航速 15 kn 下舵角輸入曲線圖Fig. 8　The rudder input curves for velocity of 15 knots

圖9　航速 24 kn 下舵角輸入曲線圖Fig. 9　The rudder input curves for velocity of 24 knots

5　結　語

本文針對某型船舶在不同航速情況下存在模型參數不確定性和風浪流的干擾問題，提出一種基于分數階 PIλDμ的航向控制算法并進行不同航速下仿真對比實驗。仿真結果表明，該算法在滿足控制精度的基礎上，具有較好的動態特性和魯棒性，對模型的攝動具有良好的適應性，可較好地應用于船舶的航向控制。

［1］范尚雍. 船舶操縱性［M］. 北京： 國防工業出版社， 1988：30-31.

［2］吳金波， 李天奇. 基于交叉耦合的浮筏舉升系統模糊PI同步控制［J］. 艦船科學技術， 2015， 37（12）： 33-37. WU Jin-bo， LI Tian-qi. Synchronized fuzzy PI control for raft lifting system based on cross-coupling［J］. Ship Science and Technology， 2015， 37（12）： 33-37.

［3］PEREZ T. Ship motion control： Course keeping and roll stabilisation using rudder and fins［M］. London： Springer， 2005：107-109.

［4］金鴻章， 李國斌. 船舶特種裝置控制系統［M］. 北京： 國防工業出版社， 1995： 1-5.

［5］CHISLETT M S， STR?EM-TEJSEN J. Planar motion mechanism tests and full-scale steering and maneuvering predictions for a mariner class vessel， technical report Hy-6［M］. Lyngby， Denmark： Hydro- and Aerodynamics Laboratory， 1965：1-41.

［6］王春陽， 李明秋， 姜淑華， 等. 分數階控制系統設計［M］. 北京：國防工業出版社， 2014： 5-15.

［7］DORCAK L. Numerical models for the simulation of the fractional-order control systems［R］. UEF-04-94， Kosice， 1994：arXiv：math/0204108.

［8］PODLUBNY I. Fractional differential equations［M］. New York： Academic Press， 1998： 243-259.

［9］劉勝. 現代船舶控制工程［M］. 北京： 科學出版社， 2010：34-37.

［10］曾慶山， 曹廣益， 王振濱. 分數階 控制器的仿真研究［J］. 系統仿真學報， 2004， 16（3）： 465-469， 473. ZENG Qing-shan， CAO Guang-yi， WANG Zhen-bin. Simulation research on fractional-order controller［J］. Journal of System Simulation， 2004， 16（3）： 465-469， 473.

［11］金永順. 面向魯棒運動控制系統的分數階PID控制器設計、自整定及實驗研究［D］. 長沙： 湖南大學， 2011： 1-7. JIN Yong-shun. Fractional order PID controller synthesis，auto-tuning and experiment studies for robust motion control systems［D］. Changsha： Hunan University， 2011： 1-7.

［12］盧京潮. 自動控制原理［M］. 西安： 西北工業大學出版社，2009： 135-150.

Marine course control based on fractional-order PIλDμ

ZHANG An-ming1， SUN Jie2， HUANG Jing3， LIU Jian3
（1. The Navy Representative Office in No. 426 Shipyard， Dalian 116000， China；
2. Eastern Theater Naval Armaments Department Information Systems Branch， Zhoushan 316000， China；3. Jiujiang Branch of the 707 Research Institute of CSIC， Jiujiang 332007， China）

The sailing marine vehicles are disturbed by the wind， wave and current on the ocean， which cause the model parameters' uncertainty for ship motion in different sailing velocity. In this paper， the body of ship and the disturbances of wind， wave and ocean are modeled， and a course control algorithm based on Fractional-Order PIλDμ（FOPID） to restrain the disturbance of wind and wave is proposed. The comparing numerical simulation for the dynamic model of some ship is carried out by the sea state of the 6 wind degree and 5 wave degreecompared with the conventional PID control algorithm. The numerical simulation result shows that， the algorithm proposed guarantee pretty nice control quality and robustness for different sailing speeds， and is adaptive to the disturbance of wind and wave， which can be applied to the course control of ship， and is not complicated to apply in engineering .

ship modeling；course control；fractional-order PIλDμ

V249.122+.2

A

1672-7619（2016）05-0087-04

10.3404/j.issn.1672-7619.2016.05.019

2016-02-03；

2016-03-07

張安明（1976-），男，碩士，工程師，研究方向為艦船控制、分數階及艦船建造。