三角形中有關中點問題的解題策略

楊樹艷

?

三角形中有關中點問題的解題策略

楊樹艷

數學是思維的體操，聯想是一種非常重要的思維品質，善于聯想是尋求解決問題的重要方法.當你遇到三角形中有關中點的問題時，你會產生哪些聯想呢？但愿本文能給你帶來一定的啟示.

一、遇到等腰三角形底邊上的中點聯想到“三線合一”

例1 如圖1，在△ABC中，AB=AC=5，BC=6，點M為BC中點，MN⊥AC于點N，則MN等于（）.

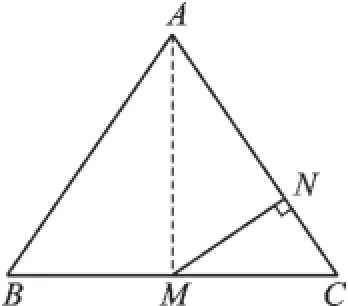
圖1

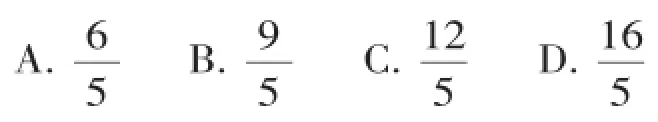
【分析】連接AM，根據等腰三角形三線合一的性質得到AM⊥BC，根據勾股定理求得AM的長，再根據直角三角形的面積公式即可求得MN的長.

解：連接AM，∵AB=AC，點M為BC中點，

∴AM⊥CM，BM=CM（三線合一），

∵AB=AC=5，BC=6，∴BM=CM=3，

在Rt△ABM中，AB=5，BM=3，根據勾股定理得：

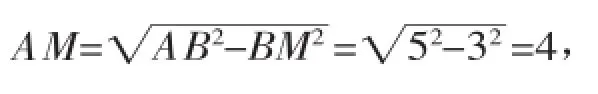
二、遇到直角三角形斜邊上的中點聯想到“斜邊上的中線，等于斜邊的一半”

例2（2015·宿遷）如圖2，在Rt△ABC中，∠ACB= 90°，點D，E，F分別為AB，AC，BC的中點.若CD=5，則EF的長為_______.

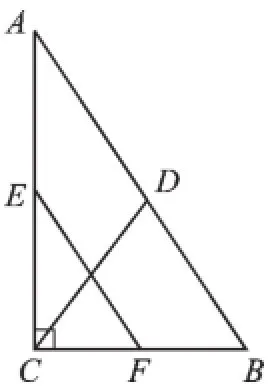
圖2

【分析】已知CD是Rt△ABC斜邊AB的中線，那么AB=2CD.EF是△ABC的中位線，則EF應等于AB的一半.

解：∵△ABC是直角三角形，

CD是斜邊上的中線，

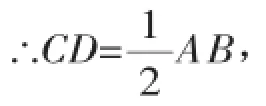
∴AB=2CD=2×5=10，

∵EF是△ABC的中位線，

三、遇到三角形中兩邊的中點，聯想“三角形的中位線定理”

例3（2015·無錫）已知：如圖3，AD、BE分別是△ABC的中線和角平分線，AD⊥BE，AD=BE=6，則AC的長等于_______.

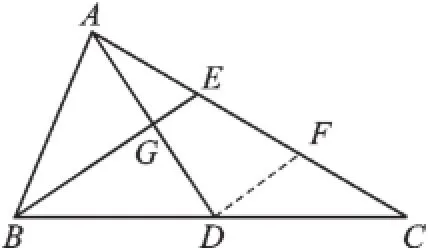
圖3

解：過D點作DF∥BE，

∵AD是△ABC的中線，AD⊥BE，

∴F為EC中點，AD⊥DF.

∵AD=BE=6，

∵BE是△ABC的角平分線，AD⊥BE，

∴△ABG≌△DBG，

∴G、E分別為AD、AF的中點.

例4（2015·巴中）如圖4，在△ABC中，AB=5，AC=3，AD、AE分別為△ABC的中線和角平分線，過點C作CH⊥AE于點H，并延長交AB于點F，連接DH，則線段DH的長為_______.

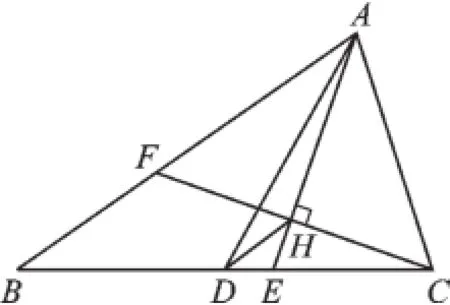
圖4

【分析】首先證明△ACF是等腰三角形，則AF=AC=3，HF=CH，則DH是△BCF的中位線，利用三角形的中位線定理即可求解.

解：∵AE為△ABC的角平分線，CH⊥AE，∴△ACF是等腰三角形，∴AF=AC，

∵AC=3，∴AF=AC=3，HF=CH，又AD為△ABC的中線，

∵AB=5，

∴BF=AB-AF=5-3=2，

∴DH=1.故答案為：1.

四、兩條線段相等，為全等提供條件（遇到兩平行線截得線段的中點時，常聯想“八字型”全等三角形）

例5 如圖5（甲），在正方形ABCD和正方形CGEF（CG＞BC）中，點B、C、G在同一直線上，M是AE的中點.

（1）探究線段MD、MF的位置及數量關系，并證明；

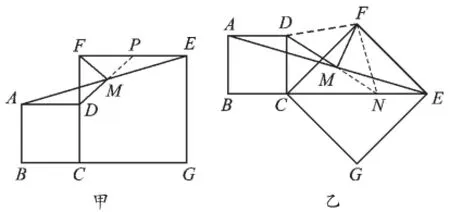
圖5

（2）將圖5（甲）中的正方形CGEF繞點C順時針旋轉，使正方形CGEF的對角線CE恰好與正方形ABCD的邊BC在同一直線上，得圖5（乙）原問題中的其他條件不變. （1）中得到的兩個結論是否發生變化？寫出你的猜想并加以證明.

【分析】（1）延長DM交EF于點P，由AM= EM，可證△ADM≌△EPM，得DM=PM，根據△DFP是直角三角形即可解題；

（2）延長DM交CE于點N，連接FN、DF，易證∠DAM=∠NEM，可證△ADM≌△ENM，得EN=AD，DM=MN，可證CD=EN，即可證明△CDF≌△ENF，得DF=NF，即可解題.

解：（1）MF⊥DM，MF=DM.

證明如下：

延長DM交EF于點P，

∵正方形ABCD和正方形FCGE，

∴AD∥EF，∠MAD=∠MEP，

∠CFE=90°.

∴△DFP是直角三角形.

∵M為AE的中點，∴AM=EM.

在△ADM和△EPM中，

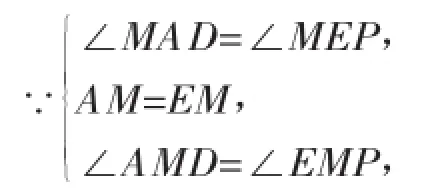
∴△ADM≌△EPM（ASA），

∴DM=PM，∴M是DP的中點，

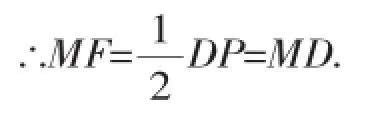
∵FD=CF-CD=CF-AD=EF-PE=PF，

∴△DFP是等腰直角三角形，

∴FM⊥DM.

（2）結論依舊成立，證明如下：

延長DM交CE于點N，連接FN、DF，

∵CE是正方形CFEG的對角線，

∴∠FCN=∠CEF=45°，

∵∠DCE=90°，∴∠DCF=45°，

∵AD∥BC，∴∠DAM=∠NEM，

在△ADM和△ENM中，

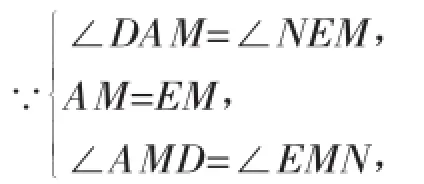
∴△ADM≌△ENM（ASA），

∴EN=AD，DM=MN，

∵AD=CD，∴CD=EN，

在△CDF和△ENF，

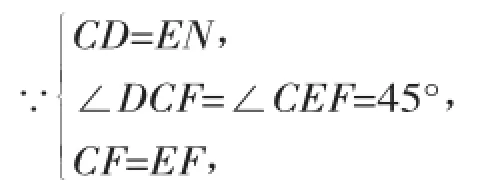
∴△CDF≌△ENF（SAS），

∴DF=NF，∠DFC=∠NFE，

又∵∠CFE=90°，

∴∠DFN=90°，

∴△DFN是等腰直角三角形，

∴DM=FM，DM⊥FM.

會學比學會更重要，方法比知識更重要.要解決三角形中有關中點的問題就必須學會聯想，通過作輔助線創造條件，運用等腰三角形底邊中線、直角三角形斜邊中線、三角形中位線的性質或倍長中線法構造全等三角形等與中點有關的策略解決問題.

（作者單位：江蘇省鹽城市明達中學）