“圓”中錯解,你有過嗎?
趙萍萍
?
“圓”中錯解,你有過嗎?
趙萍萍
圓的學習,概念繁多,性質與判定交叉復雜,不少定理又有限制條件或前提條件,而且圓還具有多種對稱性質,使得與圓有關的角、弦等位置關系充滿著多種可能性,初學圓或綜合起來解圓的習題時,有些同學就容易混淆概念或忽略不同情形,造成漏解、錯解,下面我們做一些易錯題盤點.
易錯點1一條弦所對圓周角的值有兩個,忽略其中一個
例1在半徑為r的圓內,求長為r的弦所對的圓周角.
【錯解】如圖1所示,⊙O的半徑為r,AB= r,∠ACB為弦AB所對的圓周角,連接OA,OB,則OA=OB=AB=r,
∴△OAB為等邊三角形,
∴∠AOB=60°,

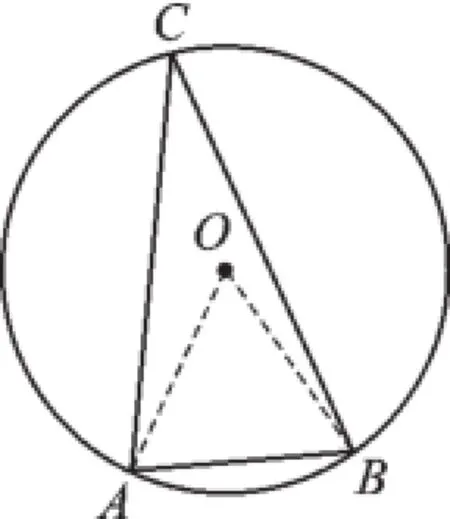
圖1
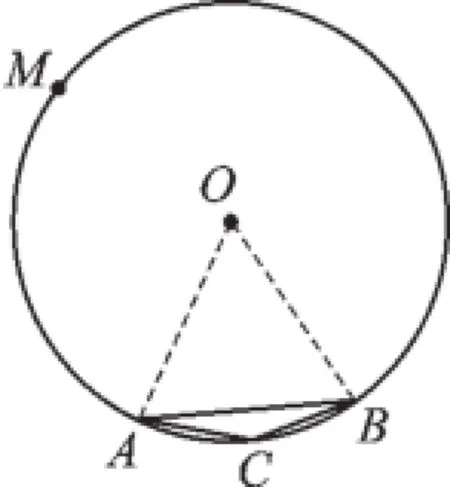
圖2
【錯解分析】產生錯解的原因是只考慮了長為r的弦所對的圓周角的頂點在優弧上,卻忽略了圓周角的頂點在劣弧上的情況.
【正解】如圖1,當圓周角的頂點在優弧上時,同上;如圖2,當圓周角的頂點在劣弧上時,∠ACB=180°-30°=150°.
易錯點2證明切線時理由不充足,表達不規范
例2 如圖3,已知△ABC中,∠C=90°,AC=BC,D,E分別是AC,BC的中點,⊙O是△DCE的外接圓.求證:AB是⊙O的切線.

圖3
【錯解】連接CO并延長交直線AB于F,
∵AC=BC,D,E分別為AC,BC之中點,
∴DC=EC=AD=BE,
∴DE∥AB,
∴O為CF中點,即有OF=OC,
∴AB為⊙O的切線.
【錯解分析】證明中雖有OF=OC,但沒有說明OF是圓心到直線的距離,理由不充足.
【正解】連接CO并延長交直線AB于F,
∵∠C=90°,∴DE為直徑,點O在DE上.
∵AC=BC,D,E分別是AC,BC的中點,
∴CD=CE,DE∥AB,
∴O為CF中點,即OC=OF.
∵DE為⊙O的直徑,OD=OE,
∴CO⊥DE,
∴OF⊥AB,
故AB為⊙O的切線.
易錯點3當兩圓相切時,只考慮一種情況造成漏解
例3半徑分別為1 cm和2 cm的兩圓外切,那么與這兩圓都相切且半徑為3 cm的圓的個數有().
A.2個B.3個
C.4個D.5個
【錯解】A或C.
【錯解分析】錯選A的原因是只考慮所求圓與已知兩圓外切的情形;錯選C的原因是考慮所求圓與已知兩圓都外切的情形,以及與其中一圓內切、另一圓外切的情形,漏掉了與兩圓都內切的情形.所求圓與已知兩圓的位置關系有五種情形:與兩個圓都外切,符合條件的圓有兩個;與其中一個內切,另一個外切,符合條件的圓也有兩個;與兩個都內切,符合條件的圓只有一個.
【正解】D.
易錯點4滾動問題中弧長的計算出錯
例4一個小朋友在粗糙不滑動的“Z”字型平面軌道上滾動一個半徑為10 cm的圓盤,如圖4所示,AB與CD是水平的,BC與水平面的夾角為60°,其中AB=60 cm,CD= 40 cm,BC=40 cm,請你作出該小朋友將圓盤從A點滾動到D點其圓心所經過的路線的示意圖,并求出此路線的長度.
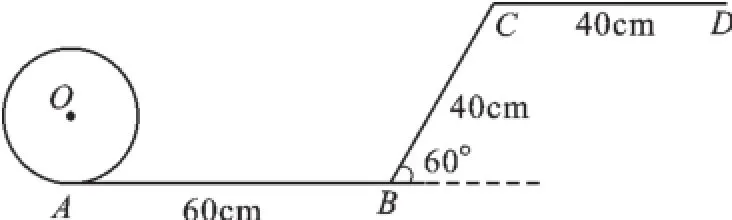
圖4
【錯解】此路線的長度為AB+BC+CD= 60+40+40=140(cm).
【錯解分析】如圖5所示,圓盤在滾動過程中圓心經過的路線由四段組成,第一段:線段OO1,第二段:線段O1O2,第三段:O2到O3的一段圓弧,第四段:線段O3O4.顯然路線長度不是線段AB、BC、CD的長度之和.
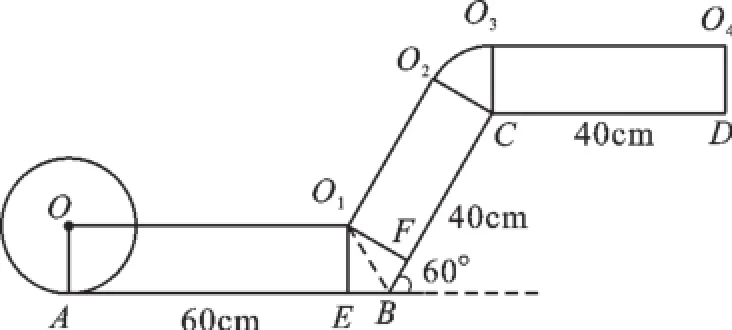
圖5
【正解】由點O1分別作O1E⊥AB,O1F⊥BC,可得∠O1BE=∠O1BF=60°,
在Rt△O1BE中,

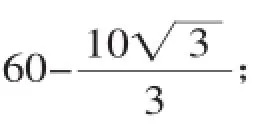
由BE=BF得,
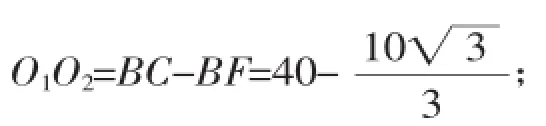
由∠O2CO3=360°-120°-2×90°=60°,

O3O4=CD=40.
所以,圓盤從A點滾動到D點其圓心所經過的路線的長度是
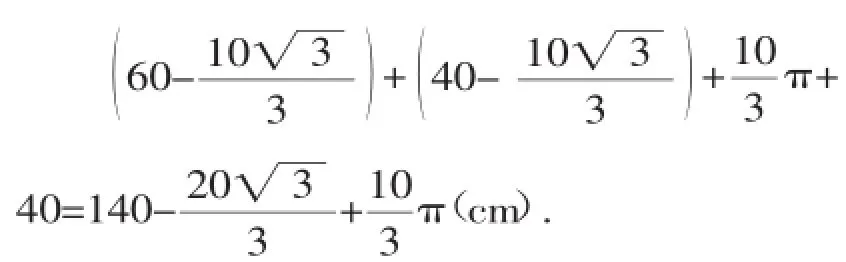
小試身手
1.(2015·黑龍江)如圖6,⊙O的半徑是2,AB是⊙O的弦,點P是弦AB上的動點,且1≤OP≤2,則弦AB所對的圓周角的度數是().
A.60°B.120°
C.60°或120°D.30°或150°
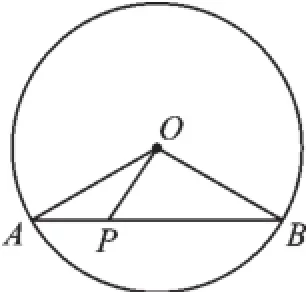
圖6
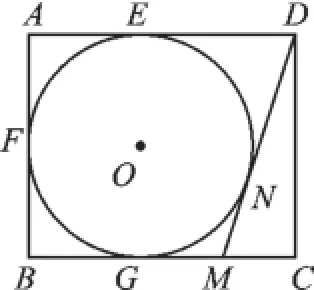
圖7
2.(2015·南京)如圖7,在矩形ABCD中,AB=4,AD=5,AD、AB、BC分別與⊙O相切于E、F、G三點,過點D作⊙O的切線交BC于點M,則DM的長為().

參考答案
1.C
2.A解:如圖8,連接OE,OF,OG,
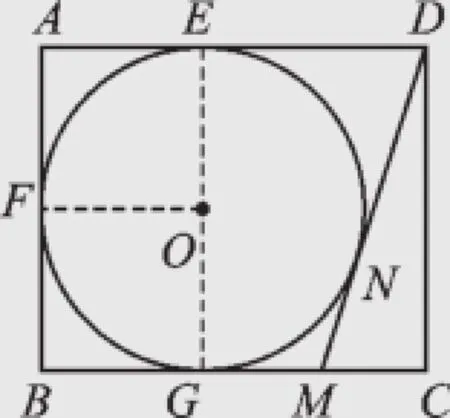
圖8
則根據矩形和切線的性質知,四邊形AEOF,FOGB都是正方形.
∵AB=4,
∴AE=AF=BF=BG=2.
∵AD=5,
∴DE=DN=3.
設GM=NM=x,
則CM=BC-BG-GM=3-x,DM=DN+NM= 3+x.
在Rt△CDM中,由勾股定理得:
DM2=CD2+CM2,即(3+x)2=42+(3-x)2,
故選A.
(作者單位:江蘇省南通市第一初級中學)

