結構性軟土粘彈塑性邊界面損傷本構模型

溫欣 ，徐東強，閆文賞，張媛

(1.河北工業大學 土木工程學院，天津 300130；2.唐山工業職業技術學院 建筑化工系，河北 唐山 063200；3.華北理工大學 建筑工程學院，河北 唐山 063000)

?

結構性軟土粘彈塑性邊界面損傷本構模型

溫欣1,2，徐東強1，閆文賞3，張媛2

(1.河北工業大學 土木工程學院，天津 300130；2.唐山工業職業技術學院 建筑化工系，河北 唐山 063200；3.華北理工大學 建筑工程學院，河北 唐山 063000)

各向異性；邊界面模型；損傷；粘彈塑性

在軟土流變性的滯后流變理論基礎上，引入考慮損傷和各向異性影響的邊界面理論，建立結構性軟土粘彈塑性邊界面損傷本構模型，并將軟土的粘彈塑性邊界面損傷模型計算結果與常規室內三軸蠕變試驗數據進行比較分析。結果表明：對應不同偏應力比，圍壓較高時的軸應力-時間曲線和孔隙水壓力-時間曲線蠕變特征明顯，圍壓較低條件計算曲線略低于對應試驗數據，表明初始作用階段模型參數設定、土樣的試驗誤差等因素誤差導致土樣初始變化具有復雜性，但總體計算模型同試驗數據基本吻合，表明模型分析的有效性。

在我國沿海地區分布著結構性和流變性特征明顯的天然軟土，大量工程實踐表明，充分理解軟土結構特性對于軟土地區地基、路基的變形預測與沉降控制具有重要影響，必須加以重視。魏星、黃茂松[1]在邊界面模型的基礎上引入各向異性張量，建立了各向異性的邊界面和硬化法則；為了考慮軟土的破損過程，孫吉主、王勇等[2]在邊界面理論的彈塑性模量中引入損傷函數，建立了結構性軟土的邊界面損傷模型；區別于傳統的Perzyna流變理論，為了更方便地描述軟土流變性，Dafalias[3]進一步提出了基于滯后變形理論的彈塑性-粘塑性理論；李興照、黃茂松等[4]將準前期固結壓力引入邊界面理論，提出了流變性軟粘土的粘彈塑性邊界面損傷本構模型。

現有流變模型研究成果多是通過完善已有模型缺陷，進而建立新的流變本構模型。該項研究通過基于修正的劍橋模型的邊界面理論，符合軟土性狀的假設以及巖土損傷理論首先構建了邊界面損傷方程，并作為滯后變形理論中的軟土塑性應變基本方程體現軟土的結構性特征，為了保證滯后粘性應變求解的概念簡單、參數意義明確，粘性應變包括的體積蠕變和剪切蠕變分別按照對應蠕變規律求解，在體現軟土結構性、流變性優點基礎上，提出一個適用于工程實踐的粘彈塑性邊界面損傷本構模型，對沿海軟土長期蠕變沉降進行預測和控制。

1 邊界面損傷方程構建

1.1邊界面方程構建

邊界面理論適用于結構性土體和流變性土體，天然粘土的結構性和各向異性是互相影響的，二者都會影響土體塑性變形的發展，為便于研究，該項研究邊界面模型做出如下假定：(1)土體結構性的形成只與顆粒間的膠結強度相關，與顆粒排列無關；(2)應力狀態落在邊界面內部或邊界面上；(3)邊界面大小由硬化規律決定；(4)彈性應變由廣義虎克定律計算；(5)假設應力作用導致結構性各向異性的改變只與顆粒排列有關，可以通過傾斜邊界面的方法表征軟土的初始各向異性；(6)邊界面上的應力點塑性應變增量大小由流動法則確定；(7)土體在邊界面內部也能產生塑性應變，塑性模量大小依賴于映射規律，也即由當前應力點與其在邊界面上的對應像應力點之間的距離確定；(8)本模型不考慮純彈性區域，采用類似修正劍橋模型的橢圓屈服面作為邊界面。

在p-q應力空間選取邊界面為橢圓見圖1，橢圓與p軸正向相交于點A (p0，0)，橢圓頂點與CSL(臨界狀態線，斜率為M)相交于頂點B，R為形狀參數，實際應力狀態(p，q)與其在邊界面上的像應力符合徑向投影規律，本文在修正劍橋模型的橢圓屈服面基礎上引入各向異性張量和損傷變量更準確的描述土體的屈服狀態，p-q空間的邊界面性狀見圖1，結構性土邊界面具體方程如(1)式：

圖1　p-q應力空間邊界面

(1)

(2-a)

(2-b)

(2-c)

(2-d)

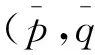
模型中涉及到的硬化內變量包括p0和aij，前者根據軟土壓縮性采用等向硬化法則，后者采取Wheeler各向異性硬化法則[4]。

(3)

式中： ψ、m為模型參數。

1.2損傷變量引入

正常固結天然軟粘土的基本特征之一是具有結構性，且不可逆，土體剛度在加載時增加，但同時因為土體損傷會發生衰減，因此呈現出相反的變形機理，因此有必要在邊界面模型中引入巖土損傷理論，定義土體損傷變量為ω。

(4)

根據Lemaitre等效應力變假設，應力作用在受損土體引起的應變與等效應力作用在無損材料上引起的應變等價，也即損傷土體的本構關系可以采用無損時的形式，因此認為損傷過程表現為土體剛度的衰減，也就是無損狀態模量的逐步衰減過程，(1-dpω)作為損傷導致的“劣化因子”被結合到粘彈塑性土體中，巖土力學材料參數損傷可用下式表示[5]：

Sd=(1-dpω)Si

(5)

1.3邊界面損傷方程構建

邊界面模型的損傷主要體現為塑性應變塑性模量Hp的衰減，引入“劣化因子”后塑性應變損傷模量Hpd表示如下：

Hpd=(1-dpω)Hp

(6)

將式(6)代入式(1)、式(3)可得各向異性邊界面損傷方程。

2 結構性軟土粘彈塑性邊界面損傷方程

方程建立基于Bjerrum提出的滯后變形理論，土體總應變由彈性應變εe，考慮損傷的塑性應變εpd和滯后應變εt構成，其中滯后應變εt又包括體積蠕變εtv和剪切蠕變εts

(1)彈性應變εe可不考慮損傷影響，由廣義胡克定律直接求取，表述如(7)式所示[6]：

(7)

(2)塑性應變εpd考慮損傷影響，由前文考慮損傷影響邊界面方程計算，表示如下：

(8)

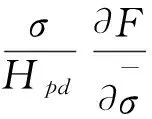
(3)滯后應變εt由體積蠕變εtv和剪切蠕變εts構成，考慮到結構性軟土蠕變的非線性特征，采用Taylor次固結理論計算體積蠕變εtv，采用Singh-Mitchell剪切蠕變公式計算剪切蠕變εts[7]。

體積蠕變率不考慮初始應變的積分變化形式為：

(9)

剪切蠕變率采用積分變化后，m≠1且不考慮初始應變的Singh-Mitchell剪切蠕變公式

(10)

(11)

3 模型特性與預測分析

唐山沿海軟土雖然按照土質分類為淤泥，但唐山沿海地基處理工程涉及的原狀土室內、室外試驗結果表明其具有一定的抗剪強度，呈現典型的結構性，為了驗證本文所提出模型的合理性，運用前面建立的考慮邊界面損傷的粘彈塑性流變模型對該海域原狀灰色淤泥質軟土進行蠕變過程進行計算，通過常規室內實測土樣的三軸蠕變不排水軸向應變和孔隙水壓力試驗，并將不同圍壓(σ3=100kPa，σ3=200kPa)、不同偏應力比(n=0.2，n=0.4)的實測土樣試驗結果同模型計算結果進行比較分析，土樣的主要物理力學指標見表1，模型參數依據可擬合曲線及經驗確定，合理的取值可提高模型計算的精度，具體選用見表2所示，與試驗數據比較結果如圖2,圖3所示，其中曲線代表理論計算結果，點符代表試驗數據。

表1　土樣的主要物理力學性質

表2　粘彈塑性流變模型計算參數

圖2　不同偏應力比軸向變形-時間試驗同計算比較

圖3　不同偏應力比孔隙水壓力-時間試驗同計算比較

從圖2、圖3結果對比可以看出，不同條件下模型計算結果同試驗數據發展規律基本吻合，不同偏應力比(n=0.2，n=0.4)條件下，高圍壓(σ3=200kPa)狀態軸應力-時間和孔隙水壓力-時間曲線蠕變趨向穩定，低圍壓(σ3=100kPa)狀態上述曲線的初始階段模擬計算值要小于試驗觀測數據，可能因素在于土體取樣時擾動影響導致以及模型初始條件設定和模型參數取值同土樣實際性能參數存在一定差異，需要對模型盡可能引入初始條件，并對模型參數進行合理性調整。

4 結論

(1)提出了考慮各向異性邊界面損傷的粘彈塑性軟土本構模型，分析假定貼近土體原始性狀，在保留了經典邊界面塑性模型的各種功能基礎上引入了各向異性張量。

(2)提出的分析模型涉及損傷因素在分析中直接體現為邊界面塑性模量的衰減，容易理解，計算方便。

(3)模型分析中通過對邊界面理論、損傷理論、滯后變形理論的合理引入，將淤泥質軟土各種特性進行耦合分析，模型計算結果同室內土工三軸試驗數據基本吻合，誤差較小，該模型建模思路清晰，模型的物理意義明確，易于被巖土工作者接受。

[1]魏星,黃茂松. 粘土的各向異性邊界面模型[J] .水利學報,2006,37(7):831-837.

[2]孫吉主,王勇,孔令偉.湛江海域結構性軟土的邊界面損傷模型研究[J].巖土力學,2006,27(1):99-101.

[3]DAFALIAS Y F. Bounding surface elastoplasticity viscoplasticity for particulate cohesive media[C]. //LUGER H J ed. Proceedingly of IUTAM Symposium on Deformation and Failure of Granular Materials. Rotterdam：A. A. Balkema,1982:97-107.

[4]李興照,黃茂松,王錄民. 流變性軟粘土的彈粘塑性邊界面本構模型[J] .巖石力學與工程學報,2007，26(7):1393-1401.

[5]柳艷華,黃茂松,李帥. 循環荷載下結構性軟粘土的各向異性邊界面模型[J] .巖土工程學報, 2010，(7): 1065-1071.

[6]Wheeler S, Naatanen A, Karstunen M. Anisotropy hardening model for normally consolidated soft clays[A]. Proc. of NUMOG VII[C]. Graz,1999.

[7]陳曉平,白世偉. 軟粘土地基粘彈塑性比奧固結的數值分析[J] .巖土工程學報, 2001,23(4):481-484.

[8]沈珠江. 理論土力學[M]. 北京:中國水利水電出版社, 2000:60-66.

[9]潘曉明,楊釗,雷春娟,等. 廣義西原粘彈塑性流變模型在ABAQUS中開發與應用[J].建筑結構學報(S2),2010，(S2):324-329.

[10]熊傳祥. 軟土結構性與軟土地基損傷數值模擬[D]. 浙江大學,2000.

Constitutive Model of Visco-elasticity Plasticity Boundary Surface Damage of Structural Soft Soil

WEN Xin1,2, XU Dong-jiang1, YAN Wen-shang3, ZHANG Yuan2

(1.Institute of Civil Engineering，Hebei University of Technology, Tianjin 300130, China；2. Department of Architecture and Chemical Engineering, Tangshan Industrial Vocational and Technical College, Tangshan Hebei 063200, China；3. College of Civil and Architectural Engineering, North China University of Science and Technology, Tangshan Hebei 063000, China)

anisotropy;boundary surface model;damage;visco-elasticity plasticity

On the basis of lagging rheological theory of soft soil rheological property,the theory of anisotropic boundary surface theory considering the effects of injury is introduced in setting up constitutive model of visco-elastic plastic boundary surface damage for structural soft soil and the model calculation results of soft soil is compared with indoor triaxial creep test data. The results of the comparison indicate: in corresponding to different deviatoric stress ratio and under the higher confining pressure the characteristics of curve about the axial stress - time curve is obvious, as well as the pore water pressure and time curve, corresponding to the test data, the calculated curve is lower than the test data under low confining pressure conditions，which shows the initial change soil sample may be complex due to model parameter setting，soil sample test error and so on，but the overall calculation model is consistent with the test data，which proves the effectiveness of the model analysis.

2095-2716(2016)03-0114-06

TU431

A