振動鉆削用階梯形變幅桿動力學性能仿真分析

李占國　劉　丹　史堯臣

(①長春理工大學機電工程學院，吉林 長春 130022；②長春大學機械工程學院，吉林 長春130022)

?

振動鉆削用階梯形變幅桿動力學性能仿真分析

李占國①②劉丹①史堯臣①②

(①長春理工大學機電工程學院，吉林 長春 130022；②長春大學機械工程學院，吉林 長春130022)

階梯形變幅桿具有結構簡單、加工方便、放大倍數大等優點，但通過傳統解析法所得變幅桿的實際諧振頻率及節點位置與理論設計值存在較大偏差，后期需進行大量修整工作。以變幅桿截面突變處添加的過渡圓弧及桿長為修整目標，利用有限元方法分析了過渡圓弧及桿長變化對放大倍數、節點位置、諧振頻率的影響規律，并得到滿足設計要求時的修整量與原有結構參數之間的函數關系式。針對某振動鉆削用階梯形變幅桿，依據函數關系式求得其修整量，并對修整后的變幅桿進行分析。結果表明：沿法蘭盤固定前后變幅桿性能參數與理論值均有較高的吻合度。

階梯形變幅桿；有限元分析；影響規律；函數關系

超聲振動鉆削技術作為一種重要的特種加工方法，有效提高了深小孔鉆削的加工精度及排屑能力。變幅桿作為超聲振動系統的重要組成部件，主要用于振幅放大及換能器與聲負載之間進行阻抗匹配[1]。常見的變幅桿有圓錐形、指數形、懸鏈形等。相對于其它形狀變幅桿，階梯形變幅桿以其結構簡單、加工方便、放大倍數大等優點受到廣泛應用[2]。變幅桿設計時要求其性能參數滿足理論設計要求，且法蘭盤固定前后無明顯變化。即變幅桿在實現固定的同時降低了因振動抑制而造成的能量損耗，從而保證超聲能量的有效傳遞。但由于傳統解析法所得階梯形變幅桿的實際節點位置及諧振頻率與理論設計值存在較大偏差，后期往往需要進行大量修整工作，使設計過程變得繁瑣[3-4]。

本文針對階梯形變幅桿，運用有限元方法分析了過渡圓弧及桿長變化對放大倍數、節點位置、諧振頻率的影響規律，并得到了相應函數關系式，從而簡化修整過程，有效地提高了變幅桿的設計效率。

1　階梯形變幅桿的理論設計

階梯形變幅桿結構如圖1所示，由兩段不同半徑的等截面圓桿組成，其中大段直徑為D，截面積為S1，長度為L1；小段直徑為d，截面積為S2，長度為L2。由于超聲波在變截面桿中的傳播可看做簡諧振動，則階梯形變幅桿縱振波動方程為：

(1)

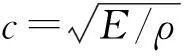
由式(1)求解得到質點位移方程：

ξ1(x)=A1cos(kx)+B1sin(kx)(-L1≤x≤0)

(2)

ξ2(x)=A2cos(kx)+B2sin(kx)(0≤x≤L2)

(3)

結合兩端自由時的邊界條件，可求得階梯形變幅桿的頻率方程、放大倍數MP、位移節點x0分別為：

S1tan(kL1)+S2tan(kL2)=0

(4)

MP=(S1sin(kL1))/(S2sin(kL2))

(5)

x0=L2-λ/4

(6)

式中：λ=c/f為縱波波長。根據式(5)、(6)求解可知，當大小段桿長均為四分之一波長時，變幅桿放大倍數達到最大，此時節點位于變幅桿的中間位置，即截面突變處。

本文針對某振動鉆削用階梯變幅桿進行設計，其理論諧振頻率f=30 kHz，材料為45鋼，材料參數如表1所示，大段直徑D=34.2 mm，小段直徑d=13.7 mm。則通過理論計算可得變幅桿大小段桿長L1=L2=L=λ/4=85.6 mm、徑長比α=D/L=0.4、大小段直徑比N=D/d=2.5、放大倍數Mp=N2=6.25。

表145鋼的材料參數

材料密度ρ/(kg/m3)彈性模量E/GPa聲速c/(m/s)泊松比μ45鋼7850207.151360.28

2　階梯形變幅桿有限元分析

運用CATIA建立上述解析法所得階梯形變幅桿的三維模型，將其導入ANSYS軟件，材料屬性根據表1定義，然后進行模態分析，得到變幅桿縱振模態下過軸線任意截面的位移分布云圖如圖2所示，并將其性能參數的仿真結果與理論值對比列于表2。

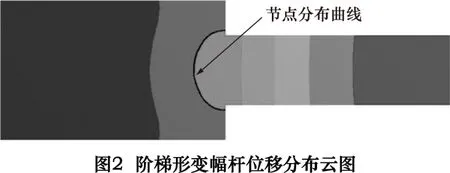
表2階梯形變幅桿性能參數對比

x0/mmf/HzMP理論值0300006.25仿真值-7.3275915.91

從所得結果可以看出，變幅桿諧振頻率仿真值遠低于理論諧振頻率；軸心節點位置向大段偏移,且過軸線任意平面內的節點分布是一條近似圓弧的不規則曲線。這是因為傳統解析法忽略了變幅桿縱振過程中截面突變處應力集中及材料的橫向振動。因傳統解析法通常將變幅桿的軸心節點視為固定節點并向外延伸設置法蘭盤進行固定，這樣勢必會抑制變幅桿的振動甚至造成損壞[5-6]。

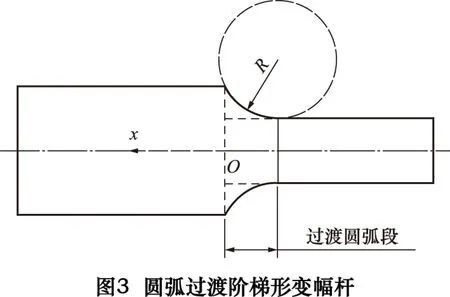
對解析法所得階梯形變幅桿進行修整時，為減小截面突變處應力集中對變幅桿諧振頻率的影響，往往在截面突變處添加過渡圓弧。當圓弧半徑小于大小段半徑差時，圓弧與突變截面及小段均相切；當圓弧半徑大于大小段半徑差時，添加方法如圖3所示，一端與變幅桿大段邊緣相交，另一端與變幅桿小段相切。法蘭盤的添加位置應選在變幅桿軸向外緣輪廓上振動位移為零的位置，即輪廓節點處。

3　階梯形變幅桿性能影響規律分析

由于變幅桿的大小段直徑需根據換能器及鉆削加工刀具系統尺寸確定，其修整一般只針對截面突變處的過渡圓弧及桿長[7]。因此本文針對振動鉆削用變幅桿，系統研究了不同N、α、f時過渡圓弧及桿長變化對變幅桿性能參數的影響規律。

3.1過渡圓弧對性能影響規律分析

取f=20 kHz、α=0.3，當N分別等于2、3、4時，對不同過渡圓弧的階梯形變幅桿進行有限元分析，得到過渡圓弧半徑R對變幅桿性能的影響規律如圖4所示。

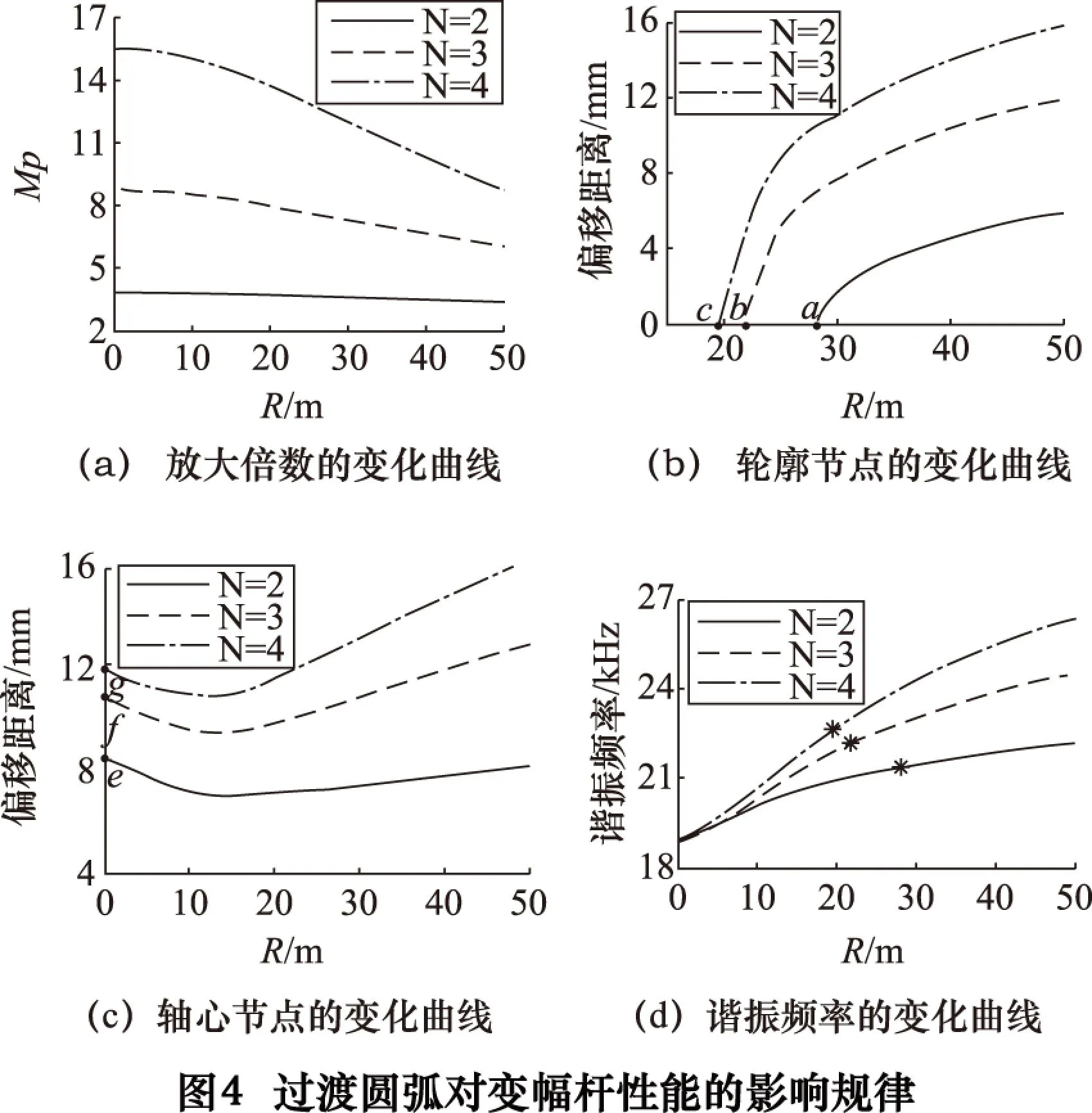
由圖4a和4b可以看出，隨R增大，變幅桿的放大倍數逐漸減小；輪廓節點沿過渡圓弧段向大段方向產生偏移，并且當R增大到某一值(a、b、c)時，輪廓節點移動到大段與過渡圓弧段交界處。由于變幅桿在輪廓節點位置需設置法蘭盤，而過渡圓弧段應力、應變分布比較復雜[8]，且考慮到此處法蘭盤加工難度等問題，輪廓節點分布于過渡圓弧段顯然是不合理的。綜合考慮，輪廓節點應位于大段與過渡圓弧段交界處，此時的過渡圓弧稱之為理想過渡圓弧，其半徑用RL表示。

對比圖4b和4c中變幅桿輪廓節點及軸心節點位置的變化情況可以看出，隨N值變化，RL(a、b、c)與無過渡圓弧時軸心節點的偏移距離x(e、f、g)在數值上存在相同變化規律。

首先對無過渡圓弧的階梯形變幅桿進行有限元分析，得到x隨N、α、f的變化規律如圖5所示。

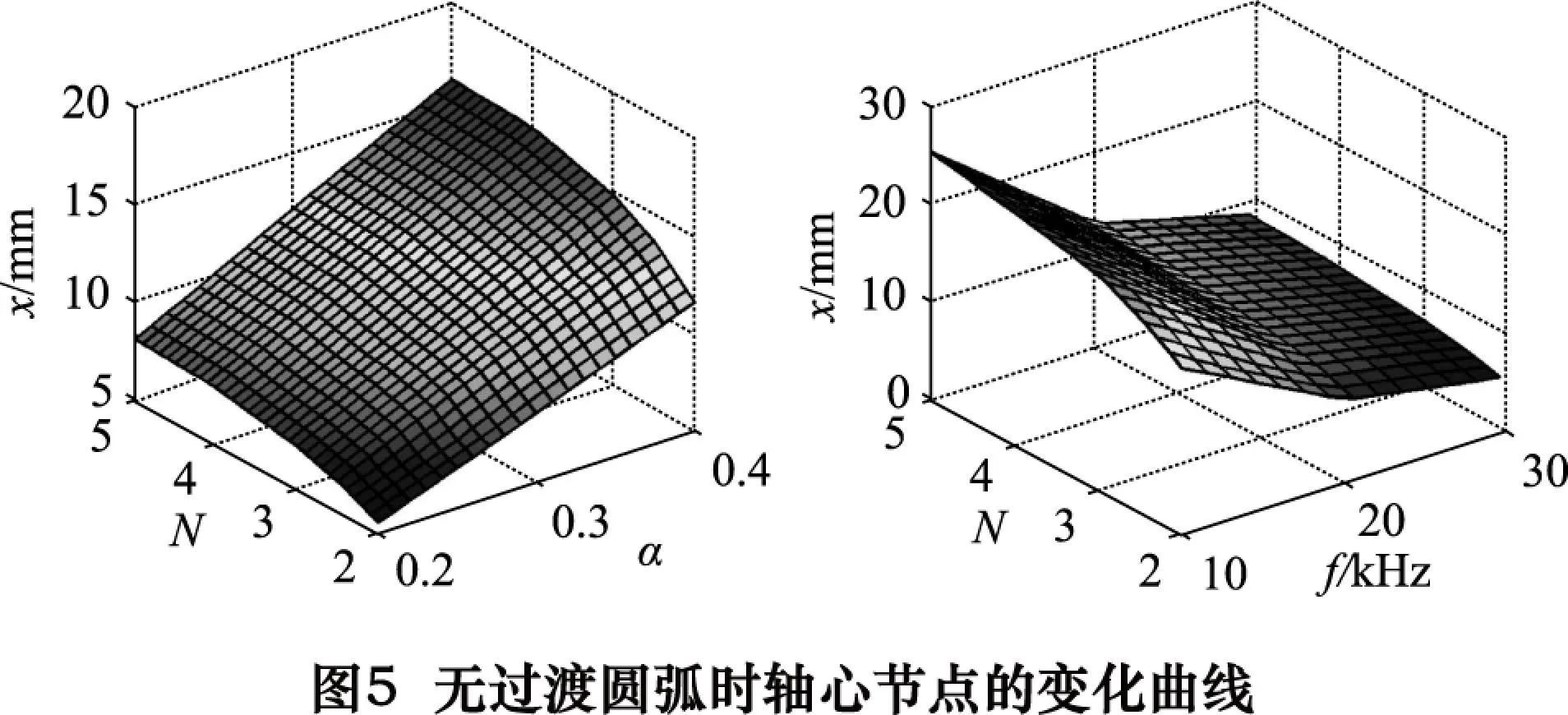
從圖5可以看出，x隨N增大而增大，增大幅度逐漸減小；與α近似于正比例關系；與f近似成反比。經整理，可將x與N、α、f間的關系可表述為：

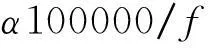
(7)

通過分析RL與無過渡圓弧時過軸線任意平面內軸心節點及截面突變處大段兩端點組成圓弧的半徑之比y的變化規律，所得結果如圖6所示。

通過上述分析可得RL與x之間的關系，整理后可將RL與N、α、f之間的關系可表述為：

(8)

通過圖4d分析可知，變幅桿的諧振頻率隨R增大逐漸增大。如圖中標記點所示，當R=RL時階梯形變幅桿的諧振頻率均大于理論諧振頻率f。經分析，添加理想過渡圓弧后的變幅桿諧振頻率相對于f的增量Δf與f的百分比變化規律如圖7所示。

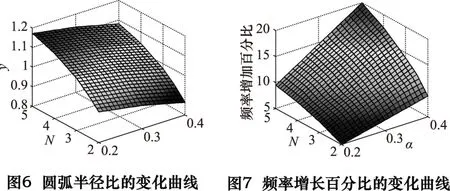
通過上述分析可將Δf與N、α、f之間的關系表述為：

Δf=[-(0.162 2-0.315α)N4+(2.078 3-3.48α)N3

-(9.387-10.68α)N2+(16.87+8α)N

-(9.39+15.6α)]f/100

(9)

3.2桿長對性能影響規律分析

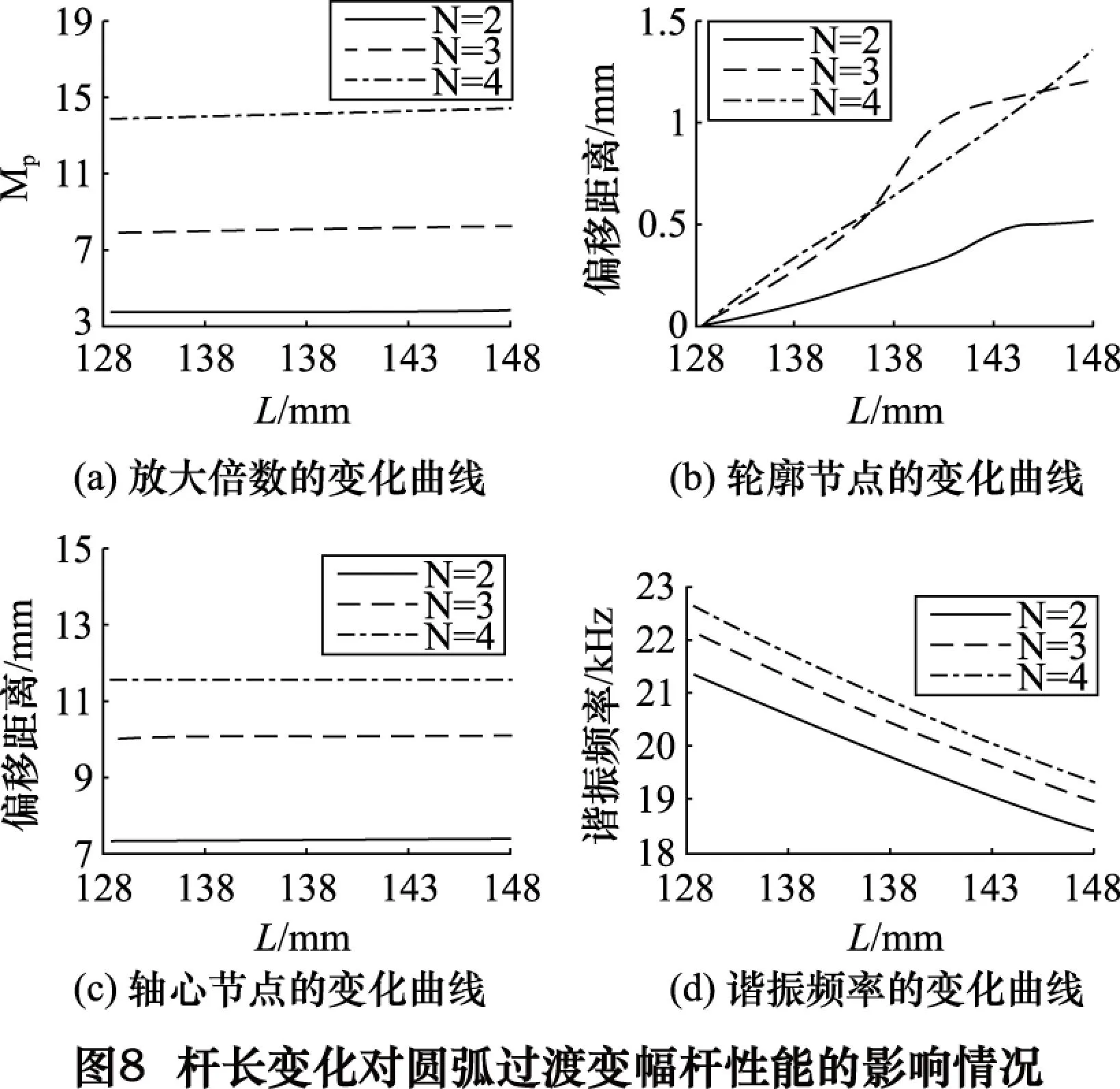
在添加理想過渡圓弧情況下，對f=20 kHz、α=0.3、N分別等于2、3、4時的階梯形變幅桿進行有限元分析，得到桿長變化對變幅桿性能的影響情況如圖8所示。其中桿長變化是指變幅桿兩端同時增加或減小某一長度。

根據圖8分析可知，隨桿長增加，變幅桿放大倍數、輪廓節點及軸心節點向大段方向的偏移量均有較小變化；諧振頻率明顯減小。為使具有理想過渡圓弧階梯形變幅桿的諧振頻率接近理論諧振頻率f，可適當調整變幅桿的桿長[7]。

針對具有理想過渡圓弧的階梯形變幅桿，將其大小段桿長同時增加或減小1 mm時所產生的頻率變化量與f的百分比δ定義為桿長變化對諧振頻率的影響系數。通過分析得知，頻率影響系數δ對N及α的敏感度相當低。在忽略兩者影響的前提下，得到δ隨f的變化規律如圖9所示。

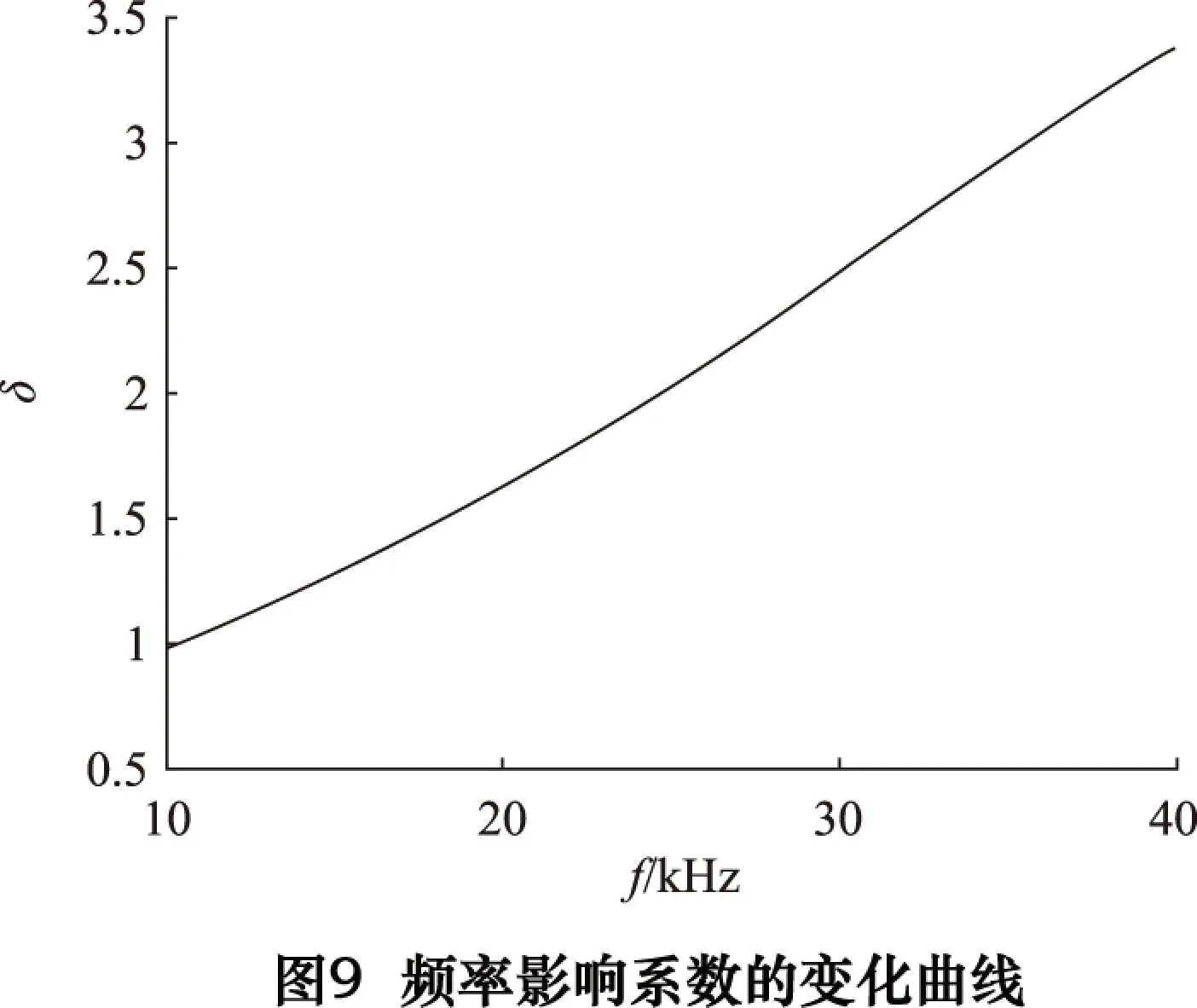
對圖9所示規律進行分析整理，得到δ與f之間的關系式為：

δ=-0.000 001 631(f/1 000)4+0.000 136 7(f/1 000)3

(10)

通過式(10)求出桿長對諧振頻率的影響系數δ，結合式(9)可得到修整后變幅桿的實際桿長：

LS=L+200Δf/(fδ)

(11)

由于變幅桿輪廓節點的位置隨桿長變化會產生微量偏移，但通過分析發現，滿足諧振頻率要求的桿長增量使輪廓節點沿軸向產生的偏移范圍內，變幅桿外緣縱振幅值與大段端面縱振幅值相差至少兩個數量級，故桿長變化對節點位置的影響可以忽略。

4　驗證

依據上述分析對第一節理論設計所得階梯形變幅桿進行修整，修整后的變幅桿桿長為95.16 mm，過渡圓弧半徑為22.9 mm,并在大段與過渡圓弧段交界處添加同樣大小的法蘭盤。對法蘭盤固定前后的變幅桿進行分析對比，對比結果如表3所示，通過傳統解析法所得變幅桿，沿法蘭盤固定前后其諧振頻率與理論值之間的偏差均比較大，放大倍數在固定前與理論值較接近，但法蘭盤固定前后變化較大；而修整后的變幅桿，沿法蘭盤固定前后其諧振頻率均接近于理論值，固定前后放大倍數變化小于6%。

表3變幅桿性能參數對比

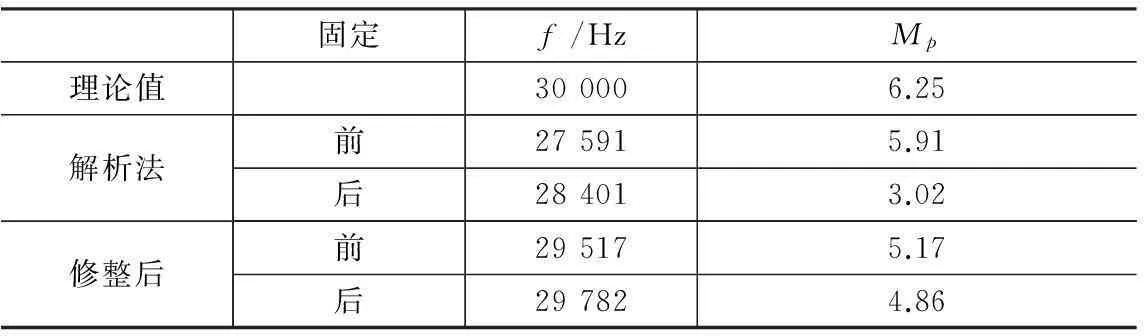
固定f/HzMp理論值300006.25解析法前275915.91后284013.02修整后前295175.17后297824.86

5　結語

(1)分析了階梯形變幅桿過渡圓弧對其放大倍數、節點位置、諧振頻率的影響規律，并得到使輪廓節點位于變幅桿大段與圓弧過渡段交界處時的理想過渡圓弧半徑RL與N、α、f之間的函數關系。

(2)分析了具有理想過渡圓弧階梯形變幅桿桿長對其放大倍數、節點位置、諧振頻率的影響規律，并得到滿足諧振頻率時桿長Ls與N、α、f之間的函數關系。

(3)針對某階梯形變幅桿，對比修整前后變幅桿性能參數，可以看出修整后的變幅桿沿法蘭盤固定前后的性能參數均接近理論值，較好地滿足了設計要求，有效地提高了變幅桿的設計效率。

[1]林仲茂. 超聲變幅桿的原理和設計[M].北京：科學出版社, 1987:53-54

[2]賈楊，沈建中. 帶過渡圓弧階梯形變幅桿的有限元分析[J]. 聲學技術，2006，25(1)：75-81

[3]趙波，許永強，鄭友益，等. 基于ANSYS的超聲變幅桿節點優化及振動性能試驗[J]. 河南理工大學學報，2014，33(3)：304-308

[4]Graham G,Petzing J N,Lucas M.Modal analysis of ultrasonic block horns by ESPI[J]. Ultrasoics, 1999(37) : 149-157.

[5]趙明利，程雪利，趙波. 帶工具頭超聲變幅桿節點定位偏差問題分析[J]. 聲學技術，2013，32(3)：253-256

[6]陳俊波. 超聲變幅桿節點優化設計[J].聲學與電子工程，2009，95(3)：23-25

[7]鄭建新，侯雅麗. 階梯形變幅桿數值設計研究[J]. 機械設計，2015，32(5)：91-94

[8]曾凡凡，王時英，呂明. 階梯形變幅桿圓弧過渡動力學分析[J]. 機械設計與制造，2012，10(10)：210-212

如果您想發表對本文的看法，請將文章編號填入讀者意見調查表中的相應位置。

Dynamic performance analysis for vibration drilling with stepped horn

LI Zanguo①②，LIU Dan①，SHI Yaochen①②

(①College of Mechanical and Electrical Engineering, Changchun University of Science and Technology,Changchun 130022, CHN; ②College of Mechanical Engineering, Changchun University, Changchun 130022, CHN)

Stepped horn has the advantages of simple structure, easy processing, high magnification and so on, but traditional analytical method of the results and theoretical design value has relatively large deviation, there are large number of repair work need by later process. Taking the transition arc and the rod length as the trimming target, the influence law of the transition arc and the length of the rod to amplification factor, node position, resonance frequency is analyzed by the finite element method, and the functional relationship between the amount of repair and the original structural parameters is obtained. Aiming at the stepped horn used in vibration drilling, the change of the amplitude of the horn is obtained according to the function relation, and analyze the trimmed horn by finite element analysis method. The results show that the amplitude transformer performance parameters are in good agreement with the theoretical values.

stepped horn; finite element analysis; influence law; function relation

TB559

A

李占國，男，1961年生，教授，博導，研究方向為現代機械設計理論與方法，已在國內外發表論文40余篇。

(編輯李靜)(2015-11-30)

160412