三軸數控機床加工誤差分析*

鄭　財　黃賢振

(東北大學機械工程與自動化學院，遼寧 沈陽110819)

?

三軸數控機床加工誤差分析*

鄭財黃賢振

(東北大學機械工程與自動化學院，遼寧 沈陽110819)

以三軸數控機床為研究對象，運用多體系統理論和齊次坐標變換，從裝配誤差、運行誤差、換刀誤差以及熱誤差這4個方面來分析數控機床加工誤差，進而建立數控機床空間誤差模型，分析出XYZ型數控機床的加工誤差。

數控機床；多體系統理論；齊次坐標變換；誤差模型

機床在機械制造工業中起到基礎性的作用，是機械制造業發展的重要保證。隨著科技的不斷進步和創新，機械設備的加工制造工藝正朝著高精度、高效率、高穩定性的方向發展。對于一些精密儀器的加工，要求加工設備具有極其高的幾何加工精度[1]。

目前，對于數控機床加工精度研究不是很成熟，大多數研究只是考慮幾何誤差和熱誤差[2-4]，同時考慮裝配誤差、運行誤差、換刀誤差以及熱誤差并建立綜合誤差模型對于數控機床加工精度的研究十分有必要。本文將XYZ型數控機床加工誤差進行更深入的分析和探討。

1　多體系統理論和齊次坐標變換

1.1多體系統理論在XYZ型數控機床中的應用

多體系統是對一般復雜機械系統的完整抽象和有效描述，是如今分析和研究復雜機械系統的最優模式。我們通過對系統的多個體進行合理的編號，然后用抽象的圖行表達系統中的各個體并滿足不同體之間的位置關系，來形成多體系統的拓撲結構[5]。

XYZ型數控機床的三維結構圖如圖1所示。

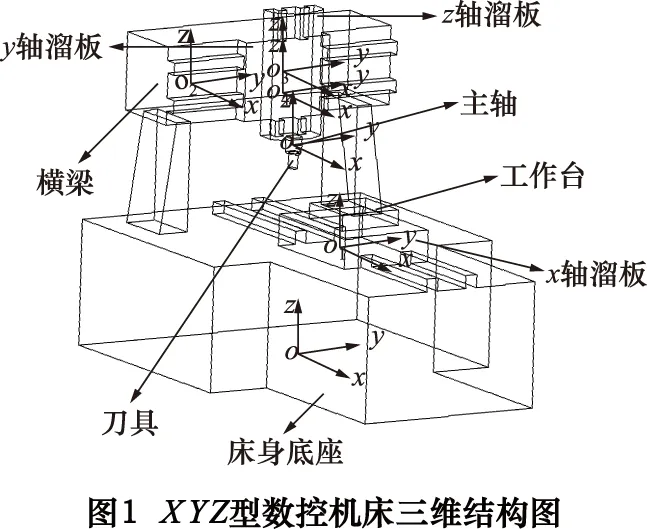
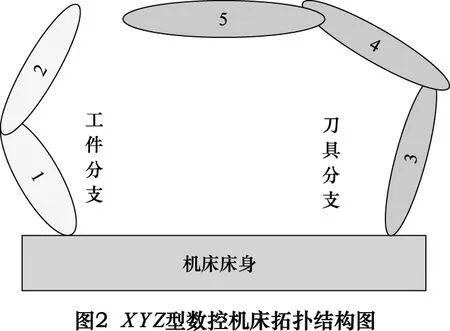
我們建立XYZ型數控機床的兩條分支：工件分支和刀具分支。拓撲結構如圖2所示。

根據圖2所示的拓撲圖，可以得到兩條誤差分支，即工件分支：床身—1—2；刀具分支：床身—3—4—5。

工件分支：圖形1代表x溜板，圖形2代表安裝在x溜板上的被加工工件。

刀具分支：圖像3代表y溜板，圖形4代表z溜板，圖形5代表刀具。

1.2齊次坐標變換理論在XYZ型數控機床中的應用

齊次坐標就是將一個原本是n維的向量用一個n+1維向量來表示。例如，二維點(x,y)的齊次坐標表示為(nx,ny,n)[6]。因此，一個向量的齊次表示并不是唯一確定的，齊次坐標的n取不同的值都表示的是同一個點，比如齊次坐標(16,8,2)、(8,4,1)表示的都是二維點(8,4)。齊次坐標系分析參考圖如圖3所示。

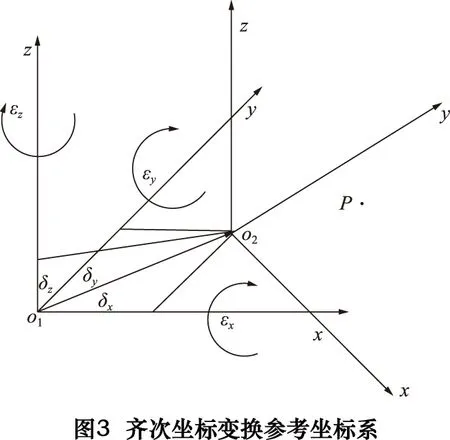
從圖3所示的坐標系中可以看出，坐標系o1、o2之間存在著一定的變化關系：將坐標系o1沿x軸移動δx，沿y軸移動δy，沿z軸移動δz，平移后的坐標系再分別繞x軸、y軸以及z軸旋轉角度εx、εy、εz即可得到坐標系o2。

坐標系o2到坐標系o1變換矩陣為：

T=TxTyTzRxRyRz

(1)

式中：Tx、Ty、Tz分別指坐標系o2到坐標系o1的移動坐標變換；Rx、Ry、Rz分別指坐標系o2坐到標系o1的旋轉坐標變換。

當位移和旋轉角度很小時，有cosε≈1、sinε≈ε，只保留一階量并進一步化簡得到：

(2)

2　XYZ型數控機床誤差分析

影響數控機床加工精度的誤差因素有很多，裝配誤差、運行誤差、換刀誤差以及熱誤差都是其影響因素。

2.1數控機床裝配誤差分析

我們分別在XYZ型數控機床的床身、x軸溜板、橫梁、y軸溜板、z軸溜板以及主軸按如下要求建立相應的坐標系(在刀具和工件上選取的參考坐標系根據實際加工情況而定)。

(1)在機床床身上建立相應的參考坐標系，并分別在x溜板、y溜板、z溜板、工作臺、橫梁、主軸、刀具以及工件上建立相應坐標系。

(2)建立在x溜板、y溜板、z溜板、工作臺、橫梁、主軸、刀具以及工件上的坐標系的x軸、y軸以及z軸方向都要和床身底座的參考坐標系的x、y、z軸向一致。

(3)建立在x溜板、y溜板、z溜板、工作臺、橫梁、主軸、刀具、工件以及底座上的坐標系的坐標原點彼此之間不重合。

(4) 要在x溜板、y溜板、z溜板、工作臺、橫梁、主軸、刀具以及工件上選取合適的點作為裝配誤差計算參考點。

通過上面的分析可以得到工件誤差分支的理論變換矩陣為：

(3)

但是由于實際裝配誤差的存在會得到工件誤差分支的實際變換矩陣為：

(4)

式中：

(5)

(6)

(7)

式中：x、y、z代指相鄰部件參考位置點間的理論坐標差值；Δx、Δy、Δz是相鄰部件參考位置點間的移動誤差差值；εx、εy、εz指旋轉誤差差值。

同理可得到刀具誤差分支的實際變換矩陣：

(8)

T(實際)=T(理論)·E

(9)

式中：E是一個綜合誤差矩陣。

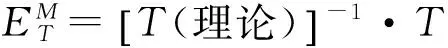
(10)

由于計算量較復雜，可以將工件分支和刀具分支的裝配誤差矩陣的表達式簡化為式(11)和(12)。

(11)

(12)

可以將總的裝配誤差定義為：

E(裝配)=E(工件)⊕E(刀具)

(13)

式中：⊕代表只把矩陣中含有字母的對應項相加，常數項不相加。

2.2數控機床運行誤差分析

根們據XYZ型機床的特點，按下面的要求建立數控機床的不同參考坐標系。

(1)在們機床床身上建立參考坐標系o，并分別建立x溜板、y溜板、z溜板、刀具以及工件的參考坐標系o1、o2、o3、T和M。

(2)x溜板、y溜板以及z溜板建立的參考坐標系的x軸、y軸以及z軸方向都要和床身底座的參考坐標系的x、y、z軸向一致。

(3)建立在刀具和被加工工件上的坐標系的x軸、y軸以及z軸方向都要和床身底座的參考坐標系的x、y、z軸向一致。

(4)根據XTYZ型機床的結構特點，在數控機床床身的合適位置選取床身底座的坐標原點。

(5)x溜板、y溜板以及z溜板建立的參考坐標系的原點o1、o2、o3和參考坐標系o的原點重合。

(6)為了便于分析，刀具和加工工件的參考坐標系的原點需要單獨建立：在刀尖處建立刀具坐標系原點，在工件底部處建立工件坐標系原點。

刀具運動鏈：機床床身—y溜板—z溜板—刀具，以及工件運動鏈：機床床身—x溜板—安裝在x溜板上的被加工工件。

在理想狀態下也就是幾何誤差不存在的情況下，刀具的實際切削點應該和編程所指示位置重合[7]，此時刀具坐標系T相對于工件坐標系W的坐標變換矩陣為：

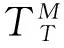
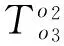
(14)

在實際加工過程中，刀具的實際切削點和理論位置會發生一定的偏移，此時刀具坐標系T相對于工件坐標系W的坐標變換矩陣為：

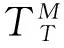
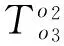
(15)

進一步分析得：

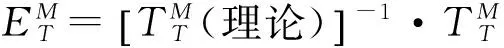
(16)

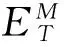
(17)

式中：Δδx、Δδy、Δδz為刀具坐標系相對于工件坐標系的位置誤差：Δθx、Δθy、Δθz為刀具坐標系相對于工件坐標系的旋轉誤差。

將不同運動鏈的具體的坐標變換矩陣代入后可得Δδx、Δδy、Δδz和Δθx、Δθy、Δθz的具體表達式。

2.3數控機床換刀誤差分析

由于數控機床在加工過程中換刀的次數與具體加工的工件有關，因此可以假設數控機床的換刀次數為n。為了便于計算，在選取合適的參考坐標系后，可以直接分析換刀一次后刀尖理想位置和實際位置的偏差。假設Δx1、Δx2、Δx3、…、Δxn為換刀后x方向的偏差，下標字母代表換刀的次數；Δy1、Δy2、Δy3、…、Δyn為換刀后y方向的偏差，下標字母代表換刀的次數；Δz1、Δz2、Δz3、…、Δzn為換刀后z方向的偏差，下標字母代表換刀的次數。

換刀n次后x軸方向總的偏移量為：

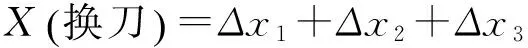
(18)

換刀n次后y軸方向的總的偏移量為：

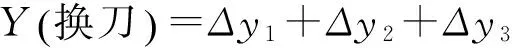
(19)

換刀n次后z軸方向的總的偏移量為：

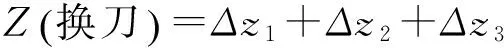
(20)

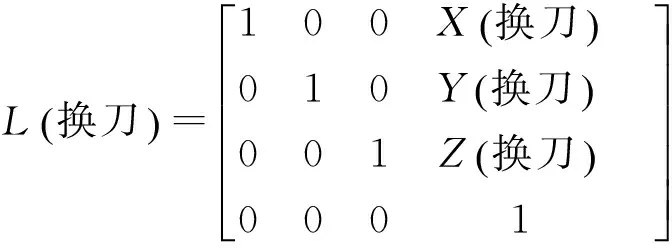
(21)

2.4數控機床熱誤差分析

數控機床在加工過程中，由于加工時機床零部件間溫度的升高，除了幾何誤差外，還會產生熱誤差。當溜板沿某一軸向運動時，由于熱轉動誤差較小一般可以忽略，所以只考慮熱漂移誤差[8]。

當數控機床的溜板沿x軸、y軸以及z軸中的某一軸運動時，會產生3個不同方向的熱漂移誤差，具體可以做以下規定：

(1)當溜板沿x軸移動時，產生的熱漂移誤差分別為lx(x)、ly(x)、lz(x)。

(2)當溜板沿y軸移動時，產生的熱漂移誤差分別為lx(y)、ly(y)、lz(y)。

(3)當溜板沿z軸移動時，產生的熱漂移誤差分別為lx(z)、ly(z)、lz(z)。

其中，下標字母x、y、z代表熱漂移誤差的方向,括號內的字母代表溜板的移動方向。

當數控機床在高速轉動時，主軸雖然會產生大量的熱量，但由于數控機床的安裝精度以及材質要求較高，在這里也只考慮主軸的3個熱漂移誤差，分別記為：lx(主)、ly(主)、lz(主)。

同樣從工件分支和刀具分支來對數控機床進行熱誤差的坐標變換。工件分支：床身—1—2；刀具分支：床身—3—4—5。

工件分支：圖形1代表x溜板，圖形2代表安裝在x溜板上的被加工工件。

刀具分支：圖像3代表y溜板，圖形4代表z溜板，圖形5代表刀具。

(22)

式中：

(23)

Δly=ly(x)+ly(y)+ly(z)+ly(主)

(24)

Δlz=lz(x)+lz(y)+lz(z)+lz(主)

(25)

3　結語

我們將數控機床誤差分為裝配誤差、運行誤差、換刀誤差以及熱誤差這四項誤差。為了便于分析，可以假設這四項誤差相互獨立，那么數控機床的綜合誤差就是這四項誤差之和。

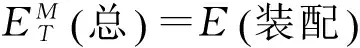
(26)

[1]袁哲俊. 精密和超精密加工技術[M].北京: 機械工業出版社, 2007:1-9.

[2]岳中軍.五軸數控機床通用幾何誤差軟件補償技術的研究[D].北京:北京工業大學，2005.

[3]張志飛.多軸數控機床熱誤差與幾何誤差建模及補償技術的研究[D].天津：天津大學，2000.

[4]童恒超, 楊建國. 數控車床兩軸聯動系統空間誤差建模技術[J].上海交通大學學報,2006, 40(7): 1213-1217.

[5]王秀山,楊建國,閆嘉鈺. 基于多體系統理論的五軸機床綜合誤差建模技術[J]. 上海交通大學學報, 2008,42(5): 761-764.

[6] 童恒超, 楊建國. 機床導軌系統空間誤差的齊次變換建模及應用[J].上海交通大學學報, 2005, 39(9): 1400-1403.

[7]王哲,趙愛國,趙德云，等.數控機床定位精度的綜合分析[J]. 機械設計與制造, 2010(9): 132-133.

[8]劉延斌,韓秀英. 雙轉臺五軸數控機床的綜合誤差建模與補償研究[J]. 機床與液壓,2008,36(4): 241-243.

(編輯譚弘穎)

如果您想發表對本文的看法，請將文章編號填入讀者意見調查表中的相應位置。

Three axis NC machine tool machining error analysis

ZHENG Cai，HUANG Zhenxian

(School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, CHN)

Based on the three axis NC machine tool as the research object, using the multi-body system theory and homogeneous coordinate transformation, from the four aspects of assembly error, error operation，tool change error and thermal error to analyze NC machine tool machining error, and the numerical control machine tool space error model, theXYZtype NC machine tool machining error.

NC machine tool；multi-body system theory；homogeneous coordinate transformation；error model

TH161.5

A

10.19287/j.cnki.1005-2402.2016.08.014

鄭財，男，1990年生，碩士研究生，從事機械可靠性設計研究。

2016-01-05)

160825

* 國家自然科學基金項目(51105062&51305071)