數控系統故障分布規律的確定與選擇*
高連生 任 增
(北京航空航天大學機械工程及自動化學院,北京 100191)
?
數控系統故障分布規律的確定與選擇*
高連生任增
(北京航空航天大學機械工程及自動化學院,北京 100191)
針對高可靠性的數控系統產品故障間隔時間樣本量少的特點,提出采用故障總時間法按故障發生的先后順序將考察的同系列多臺數控系統的樣本數據統計到一臺樣本上來考察該系列數控系統故障間隔時間的分布模型。為了增加可靠性研究的準確度,分別假設故障間隔時間同時滿足常用的四種壽命分布函數,對通過檢驗的分布模型分別采用誤差面積比指數、相關指數法以及灰關聯分析法計算樣本數據與參考分布的誤差面積比指數、相關指數以及關聯度,根據誤差面積比指數、相關指數以及關聯度的大小進行分布模型的擇優,最終確定該系列數控系統故障間隔時間服從威布爾分布。同時給出了故障率曲線,為數控系統可靠性的預測和控制提供依據。
故障間隔時間;故障總時間法;誤差面積比指數;相關指數;威布爾分布
數控系統的故障分布模型是對其進行可靠性分析的重要基礎,是一切可靠性提高工作的開端。目前國產數控系統的可靠性數據通常通過定時截尾統計試驗方案獲得。確定故障分布模型的常用數理統計方法是等時間間隔頻次法,即將統計總時間按故障發生總數劃分為若干個等時間區間,將一次考核的多臺數控機床的故障時間觀測值從小到大排序,統計落入各個區間的樣本數和頻率,以每組的區間中值為橫坐標,每組的累積失效概率的觀測值為縱坐標作累積頻率分布圖[1]。用圖估法初步判斷母體的分布類型,采用最小二乘法或極大似然法求出未知分布參數的估計值,最后采用d檢驗法或者χ2檢驗法對故障分布模型進行驗證。該方法的不足之處是當樣本數據較少時不易確定時間區間的大小,時間區間過大,則得到的散點數據較少,時間區間太小則可能導致區間內頻次為零,致使輸出的分布圖不夠精確。時間區間的確定很大程度上取決于主觀因素,需要有豐富的經驗。而且對于高可靠性的產品來說單個產品故障時間的樣本點少,得到的散點不足以判斷母體的分布類型。故障總時間法將考核的同系列多臺樣本數據統計到一臺系統上以此得到總的故障間隔時間的樣本觀測值,分別以樣本觀測值以及相應的經驗分布函數為橫、縱坐標得到故障間隔時間的累積分布函數[2]。故障總時間法能夠有效地解決樣本單個系統樣本點較少的問題。在建立分布模型的過程中,以往的研究通常是直接假設故障間隔時間服從指數分布、正態分布、威布爾分布中的一種,進行擬合分析[3]。但事實上,數控系統的故障時間可能同時滿足幾種分布為了增加可靠性研究的準確度,假設故障間隔時間同時服從正態分布、對數正態分布、指數分布、威布爾分布,分別進行分布模型的擬合,對于假設檢驗通過的分布模型同時采用相關指數法、誤差面積比指數法及灰關聯分析法確定最優的分布模型。
表1故障記錄部分數據
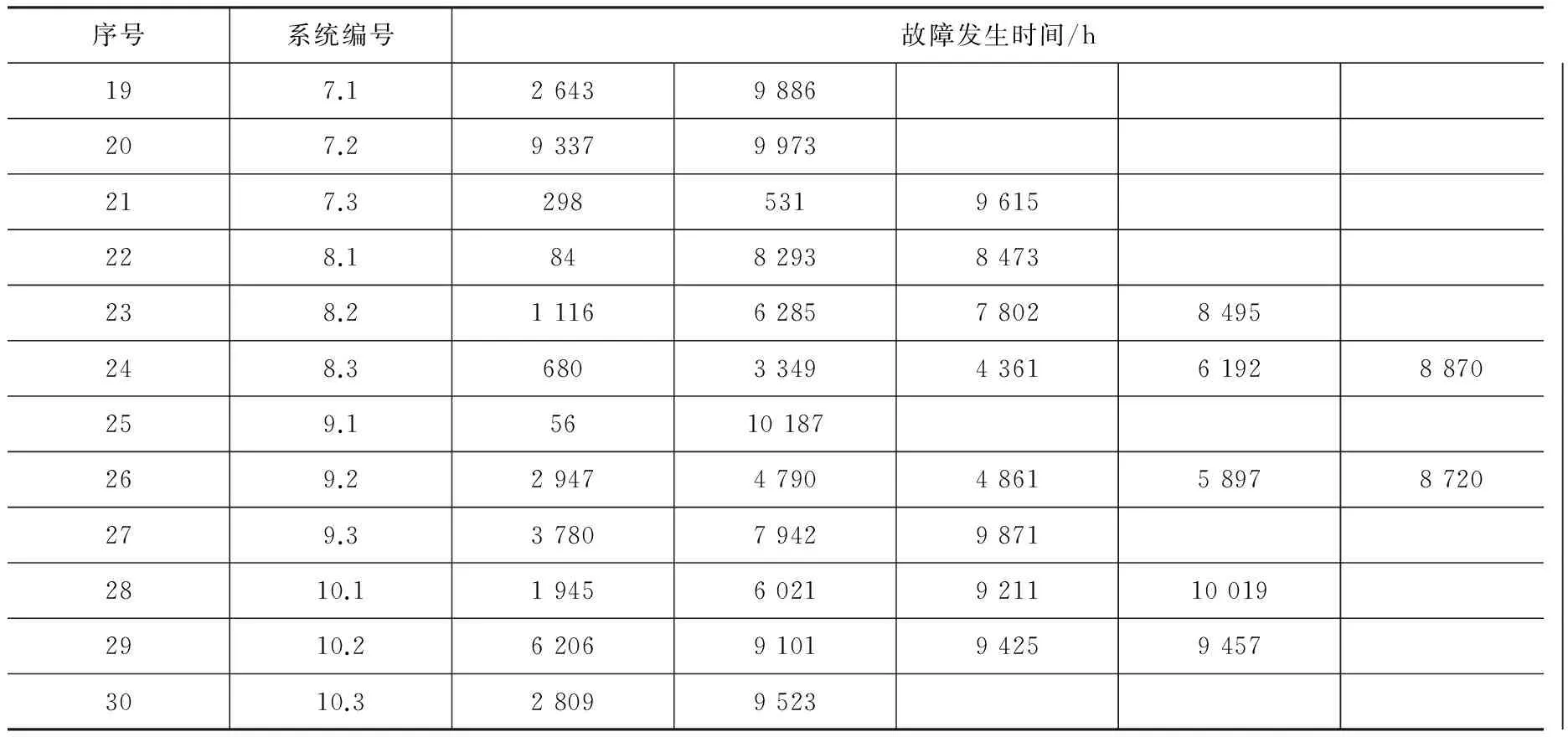
序號系統編號故障發生時間/h197.126439886207.293379973217.32985319615228.18482938473238.21116628578028495248.368033494361619288709059259.15610187269.229474790486158978720279.33780794298712810.1194560219211100192910.262069101942594573010.328099523
1 故障分布規律的初步確定
1.1故障總時間法
故障總時間法實際上是將同系列多臺系統的數據統計到一臺系統上,其計算方法如圖1所示[4]。
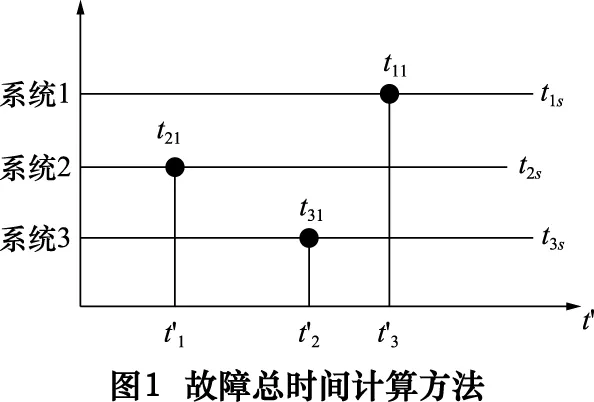
圖中,tis(i=1,2,3)為第i臺數控系統終止試驗時間;
tij為第i臺系統發生第j次故障的時間點。
各故障點的總時間計算公式分別為:
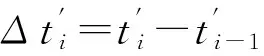
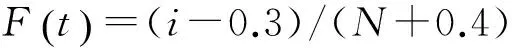
(1)
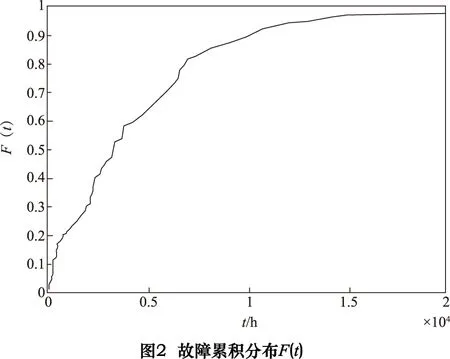
其中:i表示按失效時間點前后排列的故障序號;N表示總故障次數。
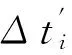
1.2故障間隔時間分布模型的擬合
①假設故障間隔時間服從正態分布
(2)
用最大似然法估計參數得:
μ=3 981.42,σ2=6 680 211
用K-S檢驗法檢驗假設:
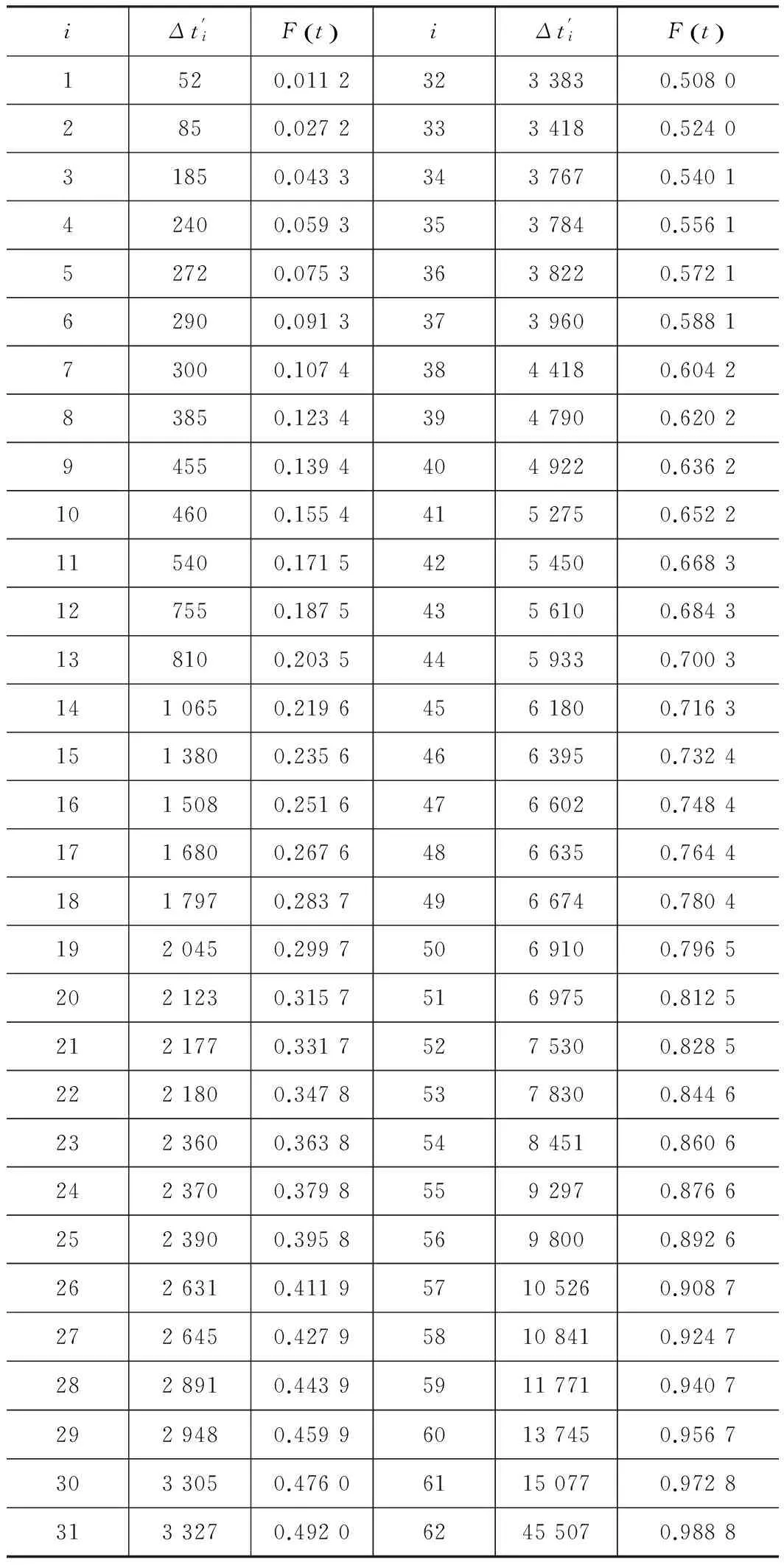
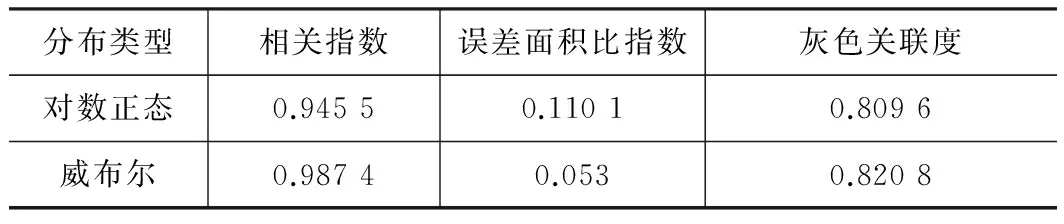
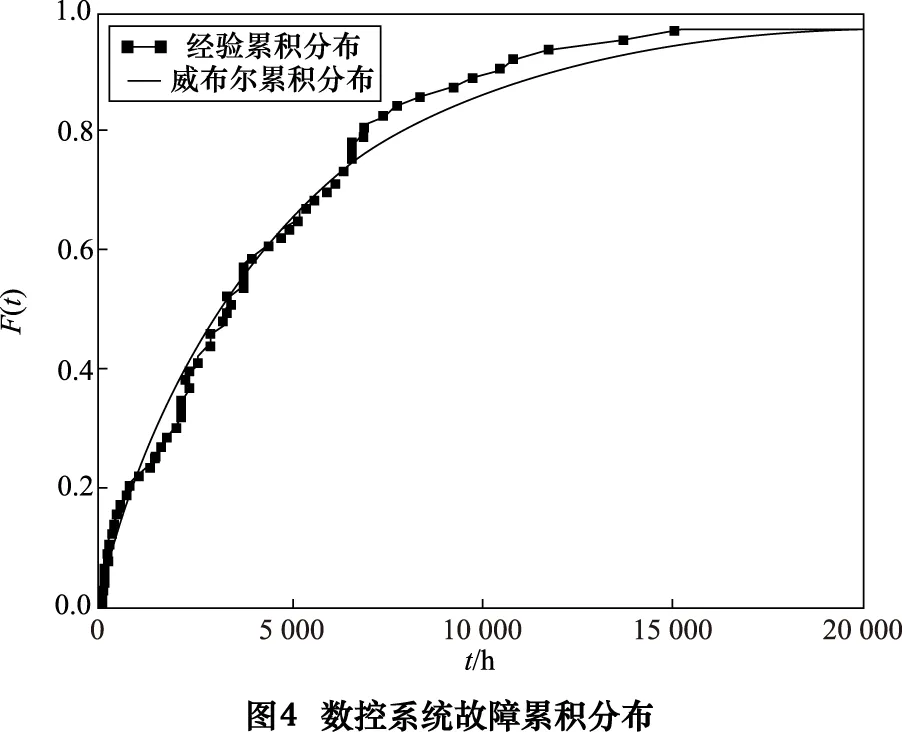
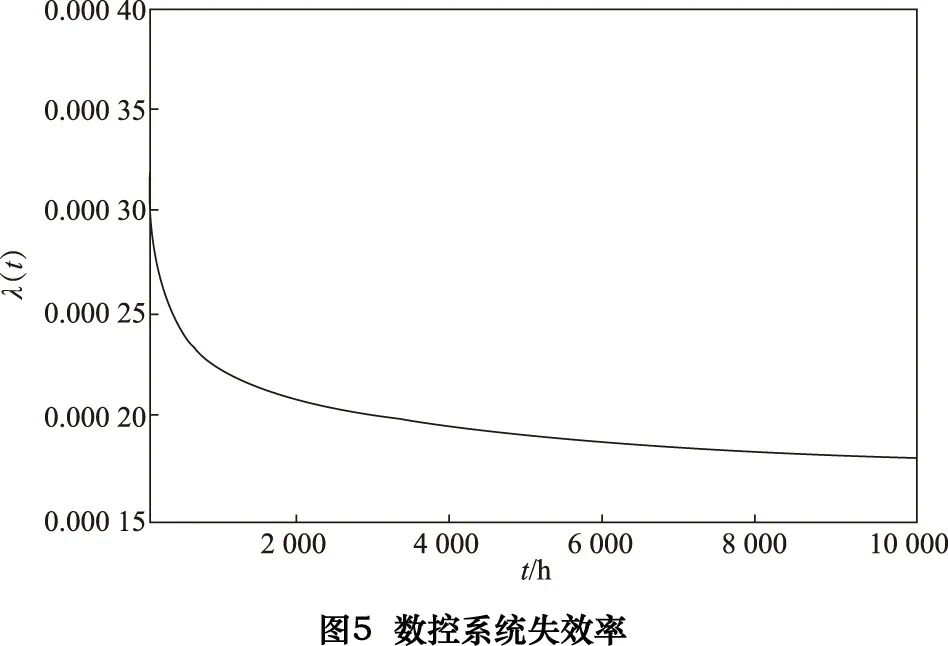
顯著度為0.1時,D(n,∝)=0.158,所以D(n,∝) ②假設故障間隔時間服從對數正態分布 (3) 用最大似然法估計參數得: μ=7.838 9,σ2=1.759 6 同上,用K-S檢驗法檢驗假設:Dn=0.135 8 顯著度為0.1時,D(n,∝)=0.158,所以D(n,∝)>Dn,故接受原假設。 表2樣本觀測值 iΔt'iFt()iΔt'iFt()1520.01123233830.50802850.02723334180.524031850.04333437670.540142400.05933537840.556152720.07533638220.572162900.09133739600.588173000.10743844180.604283850.12343947900.620294550.13944049220.6362104600.15544152750.6522115400.17154254500.6683127550.18754356100.6843138100.20354459330.70031410650.21964561800.71631513800.23564663950.73241615080.25164766020.74841716800.26764866350.76441817970.28374966740.78041920450.29975069100.79652021230.31575169750.81252121770.33175275300.82852221800.34785378300.84462323600.36385484510.86062423700.37985592970.87662523900.39585698000.89262626310.411957105260.90872726450.427958108410.92472828910.443959117710.94072929480.459960137450.95673033050.476061150770.97283133270.492062455070.9888 ③假設故障間隔時間服從指數分布 (4) ④假設故障間隔時間服從威布爾分布 (5) 用最小二乘法估計參數得m=0.910 3,η=4 712.6。用K-S檢驗法檢驗假設:Dn=0.073 9。顯著度為0.1時,D(n,∝)=0.158,所以D(n,∝)>Dn,故接受原假設。 綜上所述,在同樣的顯著度下,故障間隔時間的分布同時符合對數正態分布和威布爾分布。為了獲得最為準確的分布模型,應用相關指數法、誤差面積比指數法和灰關聯分析法定量計算,比較理論分布與經驗分布函數的相關指數以及誤差面積比指數以及灰關聯系數,得出較為準確的分布模型[5]。 2.1相關指數法 樣本數據服從所假設的分布的程度高低,能夠用相關指數R來衡量: (6) 2.2誤差面積比指數法 偏差曲線e(x)與橫坐標圍成的面積越小,說明理論曲線與實際曲線之間的偏差就越小。Se表示偏差曲線與橫坐標所圍成區域的面積[6]。則 (7) 式中n表示分割區間的個數。Se越小擬合的越好。 (8) 2.3灰色關聯度分析法 兩個系統之間的因素,其隨不同對象或時間變化而變化的關聯性大小的量度,稱為關聯度。隨著系統的發展,如果兩個因素同步變化程度較高,稱為二者關聯程度較高;反之,較低[1]。灰色關聯度分析方法,就是根據因素之間發展趨勢的相似或相異程度作為衡量因素之間關聯程度的一種方法,它不關心因素之間的偏差大小,主要關心因素發展趨勢是否一致。 灰關聯分析法在分布擬合擇優中的應用方法如下:對于時間區間[a,b],b>a≥0,令Δtk=tk-tk-1,k=2,3,…,n,Δtk>0,兩原始序列在[a,b]各點的取值分別為: (9) (10) 其中X1,X2是相同指標在各點上的值。 (1)生成增量序列 (11) (12) (2)標準化 (13) (14) (3)計算各時間點的關聯系數 (15) (16) 2.4分布模型擇優 上述三種擇優方法計算結果如表3。可以看出相關指數和誤差面積比以及灰色關聯度分析的結論是一致的,認為威布爾分布是最優的分布模型。所以綜合來看選擇威布爾分布為最優分布模型。 表3三種方法計算結果比較 分布類型相關指數誤差面積比指數灰色關聯度對數正態0.94550.11010.8096威布爾0.98740.0530.8208 (17) (18) MTBF的數學期望按下式計算: (19) 數控系統故障累積分布情況以及數控系統失效率曲線如圖4、圖5所示。 綜上所述采用故障總時間法處理同系列多臺樣本數據可以實現單臺樣本觀測值少的情況下的數據的統計分析,避免主觀因素的影響,簡化計算過程。為了提高分布模型的研究精度進行分布類型的優選是必要的。這里運用相關系數法、誤差面積比、灰關聯分析等各種擇優方法對通過K-S檢驗的失效模型進行擇優,獲取了相對準確的平均無故障間隔時間MTBF的分布模型-威布爾分布模型,并進一步計算得到了數控機床準確的可靠性指標MTBF及失效率曲線,為數控系統實施可靠性增長和制定維修計劃提供有力幫助。 [1]張英芝,賈亞洲,申桂香,等.數控機床故障分布的灰關聯分析法[J]. 農業機械學報,2004,35:195-197. [2] 于捷,賈亞洲.數控車床故障間隔時間分布模型與擬合檢驗[J]. 機床與液壓,2005(11):198-200. [3] 王興珊.包裝機械的MTBF計算和故障分析[D].無錫:江南大學,2008. [4] 張英芝,賈亞洲,張學文,等.數控沖床的故障概率分布模[J].吉林大學學報:工學版,2004(2):264-267. [5] 王興珊,錢靜.關于故障分布模型擇優方法的探討[J].機床與液壓,2008(5):208-210. [6] 張英芝,賈亞洲,申桂香,等.基于隨機截尾的數控機床故障分布模型研究[J].系統工程理論與實踐,2005(2):134-138. (編輯汪藝) 如果您想發表對本文的看法,請將文章編號填入讀者意見調查表中的相應位置。 Determination and selection of failure distribution of the CNC system GAO Liansheng, REN Zeng (Mechanical Engineering Department, Beihang University, Beijing 100191, CHN) According to the characteristic of little failure interval sample of CNC systems with high reliability, the total failure time method is put forward to count several CNC systems samples data of one series to one sample according to the order of the failure time of CNC systems to survey the failure distribution model of this series of CNC systems. In order to increase the accuracy of reliability research, time between failure are assumed to satisfy four kinds of life distribution function, the optimum distribution model is determined by applying method of error area ratio, relevant index and gray correlative analysis. According to the error area ratio, relevancy and correlation degree the optimized distribution model is confirmed to obey Weibull distribution. At the same time the failure rate curve is given which provides the basis for reliability prediction and control of CNC system. time between failures; total failure time; error area ratio index; relevant index; Weibull distribution TG659 A 10.19287/j.cnki.1005-2402.2016.07.018 高連生,男,1961年生,博士,副教授,研究方向為企業信息化、質量工程、數控系統可靠性,累計發表科研論文20余篇,其中EI收錄6篇、ISTP收錄4篇。 2016-05-18) 160829 * “高檔數控機床與基礎制造裝備”科技重大專項( 2010ZX04014-017)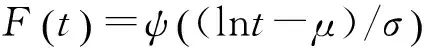
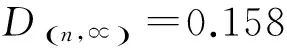
2 故障分布規律的擇優
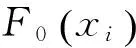
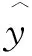
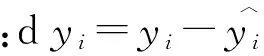
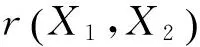
3 分布模型的確定
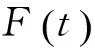
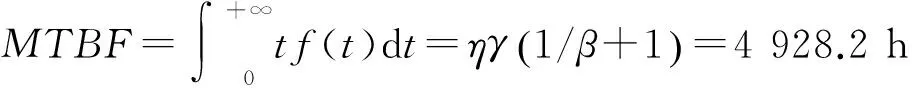
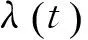
4 結語

