兩類圖在球面和環面上的嵌入

劉新求

(湖南工程職業技術學院基礎課部,中國 長沙　410151)

?

兩類圖在球面和環面上的嵌入

劉新求*

(湖南工程職業技術學院基礎課部,中國 長沙410151)

圖在不同虧格曲面上的嵌入往往有相關關系, 因此, 分析一些圖類在小虧格曲面上的嵌入是一項有意義的工作. 本文利用劉彥佩教授提出的嵌入的聯樹模型研究了兩類圖在球面和環面上的嵌入特征,分別得到了它們的嵌入個數.

曲面; 虧格; 嵌入; 聯樹

本文中關于曲面、嵌入和虧格等概念均與文獻[1]一致. 圖的曲面嵌入是拓撲圖論的一個重要分支, 特別地, 研究圖在不同虧格曲面上的嵌入個數即圖的虧格分布和完全虧格分布問題是其中重要研究方向之一. 上世紀九十年代起, 國內外很多學者做出了一些有價值的研究[2-7], 但是還遠遠未解決這個問題, 對于大部分圖類, 還不能得出其虧格分布和完全虧格分布, 此問題被證明為NP難問題. 于是, 有學者轉而研究一些圖在特定曲面上的嵌入, 譬如研究圖在球面、射影平面、環面及Klein平面等小虧格曲面上的嵌入. 近年來, 利用劉彥佩教授提出的聯樹模型和曲面運算理論[8], 國內一些學者在這方面做出了一些有意義的結論[9-11].本文作者亦在聯樹模型的基礎上, 研究了兩類項鏈圖在射影平面上的嵌入[12], 本文擬在此基礎上, 進一步研究兩類圖在球面和環面上的嵌入.

1　曲面運算理論和聯樹模型

為了表述方便, 本文對曲面運算理論和聯樹模型進行簡要介紹[8].

曲面運算理論：任何一個曲面都可以看作是由一個正多邊形“粘合”而成, 所以曲面可以用多邊形來表示, 具體的表示理論參考文獻[8]. 下面僅列出本文敘述中要用到的三種運算和三種關系.

運算1Aaa-?A.

運算2AabBab?AcBc.

運算3AB?(Aa)(a-B).

以上三種運算不改變曲面的類型. 由這三種運算, 導出曲面的三種拓撲等價關系:

關系1AaBbCa-Db-E～ADCBEaba-b-.

關系2AaBaC～AB-Caa.

關系3Aaabcb-c-～Aaabbcc.

運用以上三種運算和三種關系, 任何一個曲面都可以化為標準型代數表示:

聯樹模型[8]：聯樹模型是劉彥佩教授創立的一種研究圖的曲面嵌入的新方法. 這種方法可以如下概述: (1) 合理選擇生成樹; (2) 切斷余樹邊,得到聯樹; (3) 標記余樹邊, 按旋系走遍, 記錄余樹邊得到關聯曲面. 關聯曲面的虧格為k, 既表明在此旋系下, 圖G嵌入在虧格為k的可定向或不可定向曲面上. 圖的曲面嵌入和關聯曲面之間一一對應.

2　引理和定義

定義1若可定向曲面S=AaBbCa-Db-, 則稱邊a和b在曲面S中交錯, 若可定向曲面S=AaBa-CbDb-, 則稱邊a和b在曲面S中平行.

引理1[8]若曲面S1是可定向曲面且虧格為p, 曲面S=S1aba-b-, 則曲面S的可定向虧格為p+1.

根據引理1,S的虧格至少為1，與S是球面矛盾，所以A中邊的下標應該是從大到小，從而

充分性顯然.

從以上引理可知，一個曲面是球面當且僅當曲面中任意兩條邊均平行.

引理3[9]設A是a1,a2,…,am的線性序，曲面S=a1a2…amA～O1, 則線性序A有

種不同的排序.

定義2在兩個節點之間連結m(m≥2)條重邊構成的圖叫做雙極圖，記作Dm.

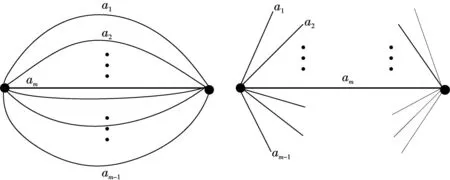
圖1　圖Dm及其聯樹Fig.1　Graph Dm and its joint tree

圖2　圖Fig.

3　主要結論

定理1雙極圖Dm在球面上的嵌入個數為(m-1)!.

證如圖1, 選擇邊am作為生成樹, 切斷余樹邊a1,a2,…,am-1, 得到聯樹. 一個點的旋有(m-1)!個, 如圖所示, 固定雙極圖左邊點的旋, 則得到雙極圖Dm的關聯曲面S=a1a2…am-1A, 其中A表示右邊點的旋, 是a1,a2,…,am-1的線性序. 根據引理2.2可知, 雙極圖Dm在球面上的嵌入個數為(m-1)!.

定理2雙極圖Dm(m≥3)在環面上的嵌入個數是

圖3　圖的聯樹Fig.3　Graph and its joint tree

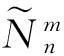
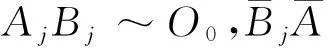
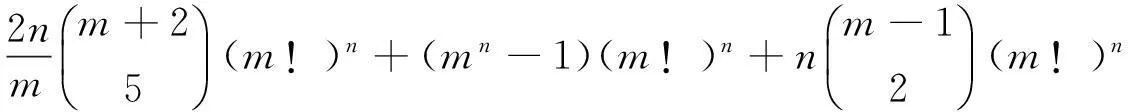
證嵌入情形1E1,E2,…,En中的每條邊均與a0平行.

同樣地, 固定節點u2i-1:i=1,2,…,n的旋, 對于i≠j, 根據引理2, 節點u2i的旋唯一確定. 所以關聯曲面中Ei(i≠j)中邊的放置方法均為m!種.

綜上, 嵌入情形1在環面上的嵌入個數為

嵌入情形2E1,E2,…,En中至少有一條邊與a0交錯.

設Ej(1≤j≤n) 中有一條邊與a0交錯, 則Ej與a0組成的子列Sj有下列子情形：

嵌入情形2.1Ej中與a0交錯的邊相互平行.

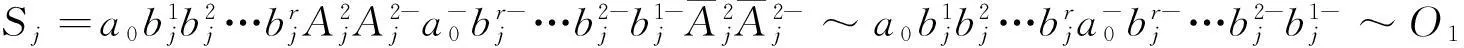
或者

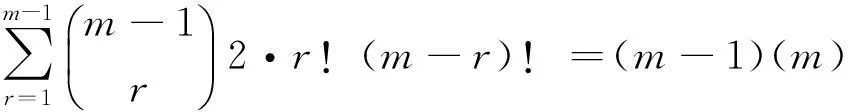
而Ei(i≠j) 的邊的放置方法有(m-1)m!+m!=mm! 種.

綜上, 嵌入情形2.1 在環面上的嵌入個數為

(mn-1)(m!)n.

嵌入情形2.2Ej中與a0交錯的邊至少有兩條互相交錯.

嵌入子情形2.2.1

方程

的非負整數解的個數為

所以Ej的邊的放置方法有

而Ei(i≠j) 的邊的放置方法均為m!, 所以此嵌入子情形在環面上的嵌入個數為

嵌入子情形2.2.2

嵌入子情形2.2.2 在環面上的嵌入個數等同于嵌入子情形2.2.1.

嵌入子情形2.2.3

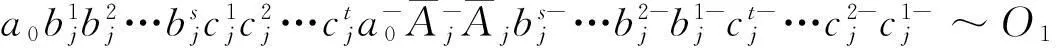
嵌入子情形2.2.3 在環面上的嵌入個數亦等同于嵌入子情形2.2.1.

則把這三種嵌入子情形相加即得到嵌入情形2.2的總嵌入個數為

把以上嵌入情形的嵌入個數相加即得定理結論.

[1]GROSS J L, TUCKER T W. Topological graph theory[M]. New York: Dover Publicaions, Inc, 1987.

[2]GROSS J L, FURST M L. Hierarchy of imbedding distribution invariants of graph[J]. J Graph Theory, 1987,11:205-220.

[3]GURST M L, GROSS J L, STATEMAN R. Genus distributions for two classes of graphs[J]. J Combin Theory Ser B, 1989,46:22-36.

[4]GROSS J L, ROBBINS D P, TUCKER T W. Genus distributions for bouquets of circles[J]. J Combin Theory Ser B, 1989,47:292-306.

[5]KWAK J H, LEE J. Genus polynomials of dippoles of circles[J]. Discrete Math, 1993,33:115-125.

[6]CHEN J, GROSS J L, RIEPER R G. Overlap matrics and total imbedding distrbution[J]. Discrete Math, 1994,128:73-94.

[7]CHEN Y C, LIU Y P. The total embedding distributions of cacti and necklaces[J]. Acta Math Sinica (Eng Ser), 2006,22(5):1583-1590.

[8]劉彥佩. 地圖的代數原理[M]. 北京：高等教育出版社, 2006.

[9]楊艷, 劉彥佩. 兩類四正則圖的完全虧格分布[J]. 數學學報, 2007,50(5):1190-1200.

[10]趙喜梅, 劉彥佩. 類圈圖的虧格分布[J]. 數學物理學報, 2008,28(4):757-767.

[11]魏白, 黃元秋, 郭婷, 等. 一類圖在小虧格曲面上的嵌入[J]. 湖南師范大學自然科學學報, 2012,35(5):24-29.

[12]劉新求, 黃元秋. 兩類項鏈圖在射影平面上的嵌入[J]. 數學物理學報, 2011,31(3):601-610.

(編輯HWJ)

The Embedding of Two Type Graphs on the Sphere and Torus

LIU Xin-qiu*

(Basic Courses Department, Hunan Vocational Technical College of Engineering, Changsha 410151, China)

Embedding numbers of graphs on distinct genus surfaces are always related. Therefore, analyzing embedding numbers of graphs on lower genus surfaces is important to determine their genus distributions and total genus distributions. Based on the model of joint tree introduced by Liu, this paper calculates the embedding number of two type graphs on sphere and torus.

surface; genus; embedding; joint tree

10.7612/j.issn.1000-2537.2016.03.013

2015-04-19基金項目：國家自然科學基金資助項目(11371133; 61370172;11471106) ；湖南省教育廳科學研究資助項目(13C200)*通訊作者,E-mail：liuxinqiuxie@sina.com

O157.5

A

1000-2537(2016)03-0075-05