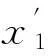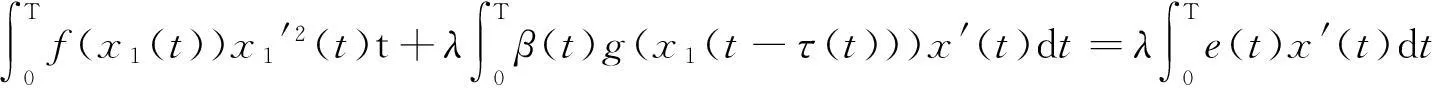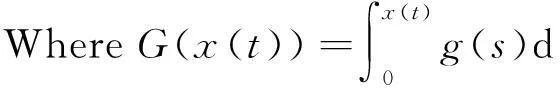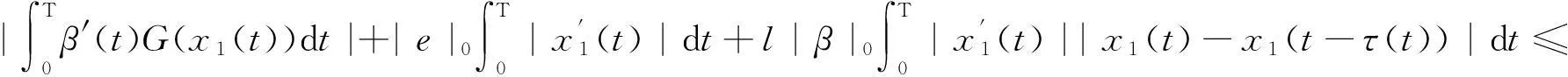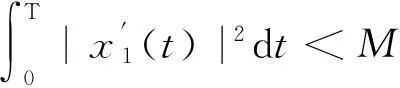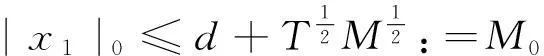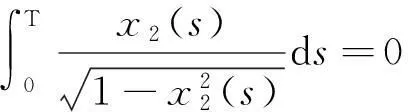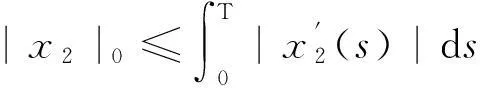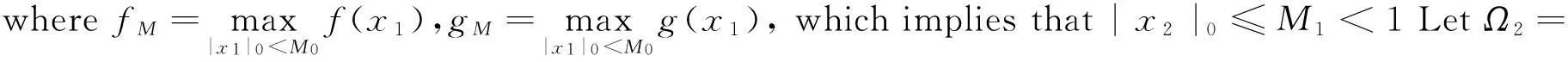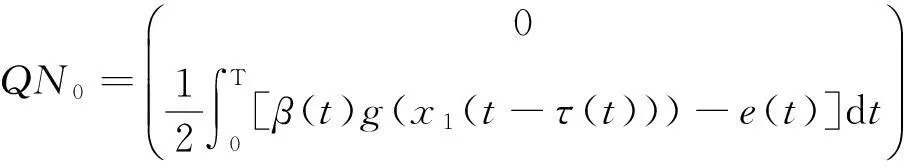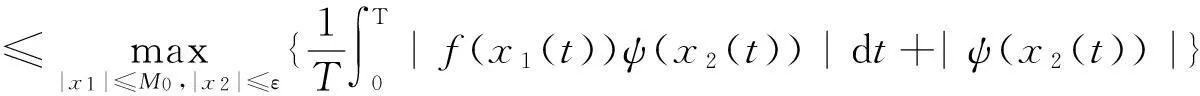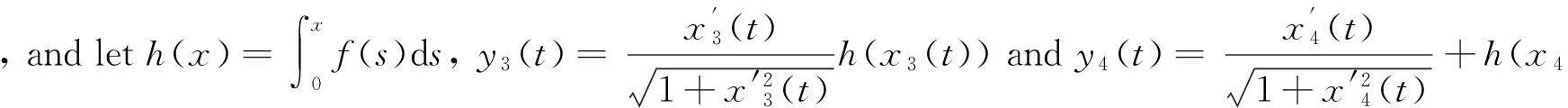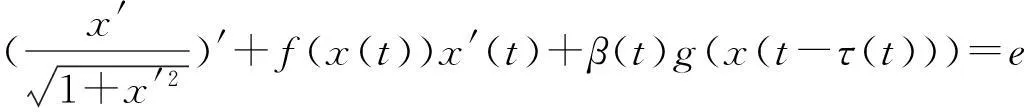一類廣義平均曲率Liénard方程周期解存在性與唯一性

蘭德新，陳文斌

(武夷學院數學與計算機學院，中國 武夷山　354300)

?

一類廣義平均曲率Liénard方程周期解存在性與唯一性

蘭德新*，陳文斌

(武夷學院數學與計算機學院，中國 武夷山354300)

運用Mawhin 重合度拓展定理研究了一類廣義平均曲率Liénard 方程

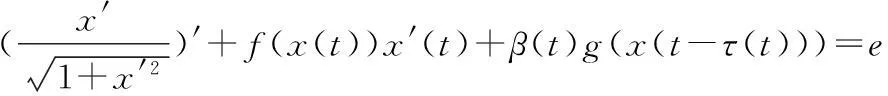
周期解存在性與唯一性問題，得到了周期解存在性與唯一性的相關新結果．

廣義平均曲率；Liénard 方程；周期解；重合度

1　Introduction

We consider the following Prescribed mean curvature Liénard equation:

(1)

wheref,e∈C(R,R),β,g,τ∈C1(R,R),e,τ,βare T-periodic,T>0,β(t)>0 andτ(t)≥0. As we all know, the dynamic behaviors of Liénard equation have been wide-ly investigated[1-5]due to the application in many fields such as physics, mechanics and the engineering technique fields. In such applications, it is important to know the existence of periodic solutions of Liénard equation. For example, see papers[1-5]. These papers were devoted mainly to study the following several types:

x″(t)+f(x(t))x′(t)+g(x(t-σ))=e(t),

x″(t)+f(x(t))x′(t)+g(x(t-τ(t,x(t))))=e(t),

(φp(x′(t)))′+f(x(t))x′(t)+β(t)g(x(t-τ(t)))=e(t).

(2)

2　Preliminaries

Throughout this paper, letXandYbe real Banach spaces and letL:D(L) ?X→Ybe a Fredholm operator with index zero; hereD(L) denotes the domain ofL.This means that ImLis closed inYand dim KerL=dim(Y/lmL)<+∞. Consider the supplementary subspacesX1andY1such thatX=KerL⊕X1andY=lmL⊕Y1and letP:X→KerLandQ:Y→Y1be the natural projections, Clearly, KerL∩(D(L)∩X1)=0; thus the restrictionLp: =L|D(L)∩X1is invertible. Denote the in-verse ofLpbyK.

(1)Lx≠λNx,?(x,λ)∈(D(L)∩?Ω)×(0,1);

(2)Nx?lmL,?x∈KerL∩?Ω;

(3) deg(JQN,Ω∩KerL,0)≠0,whereJ:lmQ→KerLis an isomorphism.

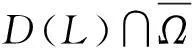
Lemma 2.2[10]Letα∈[0,+∞] be constants,S∈C(R,R) withs(t+T)≡s(t), ands(t)∈[-α,α],?t∈[0,T]. Then ?x∈C1(R,R) withx(t+T)≡x(t),we have

In order to use Mawhin’s continuation theorem to study the existence of T-periodic solutions for Eq.(1),we should consider the following system:

(3)

LetX=Y={x:x=(x1,x2)T∈C(R,R2),x(t)≡x(t+T)},‖x‖=max{|x1|0,|x2|0},

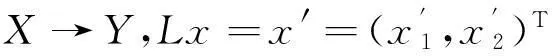
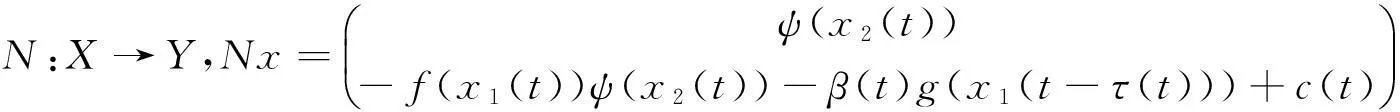
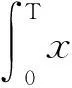
and letKrepresent the inverse ofLKer P∩D(L). Clearly, KerL=lmQ=R2and

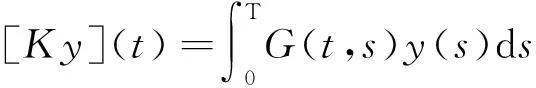
where

For the sake of convenience, we list the following assumptions which will be used for us to study the existence and uniqueness of T-periodic solutions to Eqs.(3) in Section 3.

[H2] There existsl>0 such that |g(x1)-g(x2)|≤l|x1-x2|,?l∈R,x1,x2∈R.

[H4]g′(x)<0,|τ|0≤εandτ′(t)<1 (εbe sufficiently small constant ).

3　Main results

ProofWeconsiderLx=λNx,?λ∈(0,1).

LetΩ1={x∈X:Lx=λNx,λ∈(0,1)}.Ifx∈Ω1,thenwehave

(4)

Bythefirstformulaeof(4),wehave

Itfollowsthat

(5)

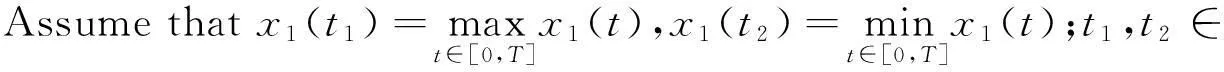
(6)

Thenfromtheassumption[H1],wemusthave

x1(t1-τ(t1))>-d,

(7)

and

x1(t2-τ(t2))

(8)

Now,webegintoprovethatthereisaconstantξ∈R such that |x1(ξ)|≤d.

Case1Ifx1(t2-τ(t2))∈(-d,d),then|x1(ξ)|≤dwhenξ=t2-τ(t2).

Case2Ifx1(t2-τ(t2))<-d,thenfrom(3.4)andthecontinuityofx1(t)onR,weseethatthereisaconstantξ∈(t1-τ(t1),t2-τ(t2))[or(t2-τ(t2),t1-τ(t1))]suchthat|x1(ξ)|=-d,i.e.,|x1(ξ)|≤d.

WeseeineitherCase1orCase2that|x1(ξ)|≤d.Sinceξ∈R is a constant, there must be an integer kand a pointt*∈[0,T] such thatξ=kT+t*.So|x1(ξ)|=|x1(t*)|≤d, which leads to

(9)

(10)

By |f(x)|≥σ, we know

(11)

(12)

By using Lemma 2.2, we see

(13)

Substituting (12) and (13) into (11). we get

(14)

Combining (9) and (14), we obtain

(15)

So by using (9), we get

Furthermore, from the first equation of (3.1), we have

Which implies that there is a constantζ∈[0,T] such thatx2(ζ)=0.So

By the second formulae of (4) and [H3], we have

Now, if we setΩ={x:x=(x1,x2)T∈X,|x1|00,equationQN(x)=(0,0)T,i.e.,

has no solution in (Ω∩KerL)/Δε, whereε∈(0,ε0) is an arbitrary constant. So deg {JQN,Ω∩KerL,0}=deg {JQN,Δε,0}. Let

Ifx∈?Δε. Then

which implies that ‖JQN(x)-JQN0(x)‖→0 asε→0. So ifε>0 is sufficiently small, then

deg {JQN,Δε,0}=deg {JQN0,Δε,0}.

Noting dimQN0=1, it follows that deg{JQN0,Δε,0}=deg{JQN0,Δ0,0}, where Δ0={x:x∈R,|x|0 is constant. By assumption [H1], we see that deg {JQN0,Δ0,0}≠0,i.e., deg {JQN,Ω∩KerL,0}=deg {JQN,Δ0,0}≠0. Then, the condition (3) of Lemma 2.1 is also satisfied. Therefore, by applying Lemma 2.1, we conclude that the equation

Lx=Nx,

Furthermore, letu(t)=x3(t)-x4(t) andv(t)=y3(t)-y4(t)v. Sincex′=ψ(y-h(x)), it follows from (1) that

we will show thatv(t)≤0,?t∈[0,T].

Suppose there exists at0∈[0,T] such thatv(t0)=maxt∈[0,T]v(t)>0 which together withβ(t)>0 implies that

(16)

It follows from [H4] and the first equation of Eq.(16) thatx3(t0-τ(t0))=x4(t0-τ(t0)), then from the second equation of Eq.(7), we get

-β(t)g′(x3(t0-τ(t0)))[ψ(y3(t0-τ(t0))-h(x3(t0-τ(t0)))-

ψ(y4(t0-τ(t0))-h(x4(t0-τ(t0)))](1-τ′(t0)).

In view ofβ(t0)>0,g′(x3(t0-τ(t0)))<0.v(t0)=y3(t0)-y4(t0)>0.τ′(t0)<1 and |τ|0<ε,εbe sufficiently small, then we haveψ(y3(t0-τ(t0)))>ψ(y4(t0-τ(t0))) andv″(t0)>0.

Which is a contradiction. Hence maxt∈[0,T]v(t)≤0. Similarly, exchanging the role ofx3andx4, we can show that maxt∈[0,T]v(t)≥0. This implies thatv(t)≡0,i.e.,y3(t)≡y4(t).Then fromg′(x)<0, we havex3(t-τ(t))≡x4(t-τ(t)).i.e.,x3(t)≡x4(t) Therefore, the Eq.(1) has at most one solution. The proof of Theorem 3.1 is now complete.

References:

[1]NGUYENPC.Periodicsolutionsofasecondordernonlinearsystem[J].JMathAnalAppl, 1997,214(1):219-232.

[2]LUSP,GEWG.PeriodicsolutionsforakindofLiénardequationwithadeviatingargument[J].JMathAnnaAppl, 2004,289(2):231-243.

[3]CHENGWS,RENJL.OntheexistenceofperiodicsolutionforP-LaplaciangeneralizedLiénardequation[J].NonlinearAnal, 2005,60(1):65-75.

[4]GAOFB,LUSP.NewresultsontheexistenceanduniquenessofpreiodicsolutionsforLiénardequationtypeP-Laplacianequation[J].JFranklinInstitute, 2008,345(2):374-381.

[5]GAOH,LIUBW.ExistenceanduniquenessofperiodicsolutionsforforcedRayleigh-typeequations[J].ApplMathComput, 2009,211(1):148-154.

[6]BONHEURED,HABETSP,OBERSNELF, et al.Classicalandnon-classicalsolutionsofaprescribedcurvatureequations[J].JDiffEqu, 2007,243(1):208-237.

[7]LOPEZR.Acomparisonresultforradialsolutionsofthemeancurvatureequation[J].ApplMathLett, 2009,22(4):860-864.

[8]PANH.One-dimensionalprescribedmeancurvatureequationwithexponentialnonlinearity[J].NonlinearAnnl, 2009,70(5):999-1010.

[9]GAINESRE,MAWHINJ.Coincidencedegreeandnonlineardifferentialequaations[M].Berlin:Springer, 1977.

[10]LUSP,GEWG.Sufficientconditionsfortheexistenceofperiodicsolutionstosomesecondorderdifferentialequationswithadeviatingargument[J].JMathAnalAppl, 2005,308(2):393-419.

(編輯CXM)

Existence and Uniqueness of Periodic Solutions for Prescribed Mean Curvature Liénard Equation with a Deviating Argument

LAN De-xin*, CHEN Wen-bin

(College of Mathematics and Computer Science, Wuyi University, Wuyi Shan 354300, China)

By using the coincidence degree theory, some new results were established, on the existence and uniqueness of T-periodic solutions for a kind of prescribed mean curvature Liénard equation of the form

prescribed mean curvature; Liénard equation; periodic solution; coincidence degree

10.7612/j.issn.1000-2537.2016.03.016

2015-10-15

武夷學院科學研究基金資助項目(XQ201305)

,E-mail：1220340699@qq.com

O175.6

A

1000-2537(2016)03-0089-06