二層隨機規(guī)劃逼近ε-最優(yōu)解集的Hausdorff收斂性

周婉娜，霍永亮，胡之英

(1.西安翻譯學院基礎(chǔ)課部大學數(shù)學教研室，中國 西安　710105；2.重慶文理學院數(shù)學與財經(jīng)學院數(shù)學研究所，中國 重慶　402160)

?

二層隨機規(guī)劃逼近ε-最優(yōu)解集的Hausdorff收斂性

周婉娜1，霍永亮2*，胡之英1

(1.西安翻譯學院基礎(chǔ)課部大學數(shù)學教研室，中國 西安710105；2.重慶文理學院數(shù)學與財經(jīng)學院數(shù)學研究所，中國 重慶402160)

二層隨機規(guī)劃是由上、下層隨機規(guī)劃組成的，下層隨機規(guī)劃是以上層決策變量為參數(shù)的隨機規(guī)劃問題，而上層是以下層隨機規(guī)劃的最優(yōu)值作為響應(yīng)的隨機規(guī)劃問題，對于此類的二層隨機規(guī)劃問題，本文首先討論了下層隨機規(guī)劃最優(yōu)值的收斂性，然后將下層隨機規(guī)劃的最優(yōu)值反饋到上層，得到了上層隨機規(guī)劃逼近ε-最優(yōu)解集序列的Hausdorff收斂性.

二層隨機規(guī)劃;ε-最優(yōu)解集; 最優(yōu)值; Hausdorff收斂性

二層規(guī)劃問題是一種具有遞階結(jié)構(gòu)的系統(tǒng)化問題，它包含上層問題和下層問題，其中上下層問題都有各自的目標函數(shù)和約束函數(shù)，二層規(guī)劃在工程設(shè)計、經(jīng)濟計劃、金融均衡和多層決策等許多領(lǐng)域的應(yīng)用起著重要的作用. 以往研究的隨機規(guī)劃[1-7]都是單層的隨機規(guī)劃問題，而且所研究的二層規(guī)劃模型[8-9]其目標函數(shù)和約束函數(shù)都是確定性的，如果二層規(guī)劃模型中目標函數(shù)和約束函數(shù)都含有不確定的隨機因素，則整個系統(tǒng)將更加復(fù)雜，且更具有實際應(yīng)用價值，這也正是本文所要研究的一類二層隨機規(guī)劃問題.

本文考慮如下的二層隨機規(guī)劃問題：

(1a)

s.t.∫Rpgj(x,y,u)μ0(du)≤0,j=1,2,…d.

(1b)

相應(yīng)的逼近問題為

(2a)

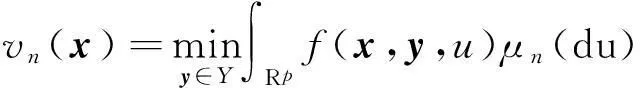
s.t.∫Rpgj(x,y,u)μn(du)≤0,j=1,2,…d.

(2b)

其中x=(x1,x2,…xn)T∈Rn，y=(y1,y2,…ym)T∈Rm，gj:Rn×Rm×Rp→R，j∈I={1,2,…d}，X∈Rn與Y∈Rm是緊凸集，F(xiàn),f是定義在Rn×Rm×Rp上的函數(shù).

1　下層隨機規(guī)劃最優(yōu)值的收斂性

為了討論上層隨機規(guī)劃問題最優(yōu)解集的收斂性，首先討論下層隨機規(guī)劃問題最優(yōu)值的收斂性.

當x0∈Rn固定時，下層規(guī)劃問題的原問題(1b)變?yōu)?/p>

s.t.∫Rpgj(x0,y,u)μ0(du)≤0,j=1,2,…d.

(3)

當xn→x0時，相應(yīng)的逼近問題變?yōu)?/p>

s.t.∫Rpgj(xn,y,u)μn(du)≤0,j=1,2,…d.

(4)

S0(x0)={y∈Y?Rm,∫Rpgj(x0,y,u)μ0(du)≤0,j=1,2…d},

Sn(xn)={y∈Y?Rm,∫Rpgj(xn,y,u)μn(du)≤0,j=1,2…d};

M0(x0)={y∈Y?Rm,∫Rpgj(x0,y,u)μ0(du)≤0,∫Rpf(x0,y,u)μ0(du)≤v0(x0)},

Mn(xn)={y∈Y?Rm,∫Rpgj(xn,y,u)μn(du)≤0,∫Rpf(xn,y,u)μn(du)≤vn(xn)}.

由文獻[10]的轉(zhuǎn)換可將問題(3)和問題(4)轉(zhuǎn)換成確定性無約束規(guī)劃問題(5)和問題(6)

(5)

(6)

2　上層隨機規(guī)劃ε-最優(yōu)解集的Hausdorff收斂性

上層隨機規(guī)劃的原問題改寫為

(7)

相應(yīng)的逼近問題改寫為

(8)

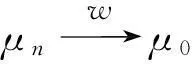
設(shè)Rn為n維歐式空間集合A?Rn到集合B?Rn的Hausdorff 距離定義為

dH(A,B)=max{e(A,B),e(B,A)},

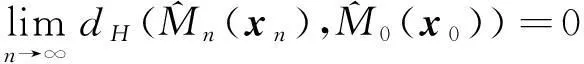
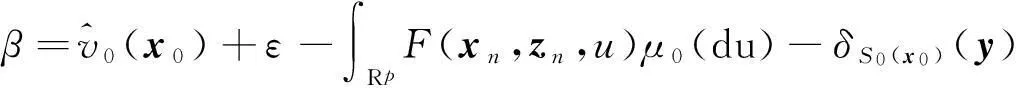
綜上有

[1]ROGER W. Stochastic Programming[M].Amsterdam: Elsevier Science Publisher, 1989.

[2]駱建文，魯世杰.隨機規(guī)劃逼近解的收斂性 [J].浙江大學學報(理學版)， 2000，27(5)：493-497.

[3]LUO J. Stability analysis for stochastic optimization problems[J]. Shanghai Jiaotong University (Science), 2007，12(5)：684-687.

[4]ROMISH W, SCHULTZ R. Stability analysis for stochastic programs[J]. Ann Oper Res, 1991,30(1)：241-266.

[5]DUPATCOVA J, GROWE-KUSKA N, ROMISH W. Scenario reduction in stochastic programming: an approach using probability metric[J].Math Progr, 2003,95(3):493-511.

[6]霍永亮，劉三陽. 隨機規(guī)劃逼近最優(yōu)解集的上半收斂性[J].西安電子科技大學學報， 2005，32(6)：953-957.

[7]霍永亮. 隨機規(guī)劃穩(wěn)定性理論[M].成都：西南交通大學出版社， 2010.

[8]萬仲平，吳國民，陳開周.一類二層規(guī)劃的上圖收斂性[J].運籌學學報， 1998，2(24)：48-53.

[9]萬仲平.關(guān)于二層規(guī)劃的逼近問題[J].系統(tǒng)科學與數(shù)學， 2000，20(3)：289-294.

[10]周婉娜，霍永亮. 二層隨機規(guī)劃逼近最優(yōu)解集的穩(wěn)定性分析[J]. 重慶工商大學學報(自然科學版)， 2013，30(7)：19-23.

(編輯HWJ)

The Hausdorff Convergence of the Optimal Solution Set of Approximation for Bi-Level Stochastic Programming

ZHOU Wan-na1, HUO Yong-liang2*, HU Zhi-ying1

(1.Department of Basic Courses, Xi’an Fanyi University, Xi’an 710105,China;2. College of Mathematics and Finance, Institute of Mathematics,Chongqing University of Arts and Sciences, Chongqing 402160, China)

Bi-level stochastic programming is through upper and lower levels of stochastic programming. The lower level stochastic programming uses the upper decision variables as the parameters of stochastic programming problems. The upper level stochastic programming is a stochastic programming problem including a parametric optimal value of the lower level stochastic programming. For the bi-level stochastic programming problem, this article first discusses the optimal value convergence of lower stochastic programming, and then feedback the optimal value of lower level stochastic programming to the upper level, obtaining the Hausdorff convergence of the upper level stochastic programming approximation optimal solution sequence.

Bi-level stochastic programming; optimal solution set; optimal value; Hausdorff convergence

10.7612/j.issn.1000-2537.2016.03.014

2015-07-04基金項目：陜西省教育科學“十二五”規(guī)劃2013年度課題(SGH13460)*通訊作者,E-mail：yongliang-huo@126.com

O221.5

A

1000-2537(2016)03-0080-04