聲速測量實驗方法的改進

李天一　何沃洲　盧子璇　陳　彥　李　華

(1北京航空航天大學電子信息工程學院,北京　100191；2中國人民大學附屬中學，北京　100080；3北京航空航天大學物理科學與核能工程學院,北京　100191)

?

聲速測量實驗方法的改進

李天一1何沃洲1盧子璇2陳彥3李華3

(1北京航空航天大學電子信息工程學院,北京100191；2中國人民大學附屬中學，北京100080；3北京航空航天大學物理科學與核能工程學院,北京100191)

基于虛擬儀器的設計原理，針對振幅法測量聲速實驗中存在的問題進行了改進，設計了一個基于單片機的聲速測量實驗系統.該系統中，單片機對接收端信號進行采樣并控制端面勻速移動.采集到的數據序列傳輸到PC機進行中值濾波，由快速傅里葉變換對序列進行預處理，再進行較精確的極值點檢測，并通過線性回歸方法對結果進行校正.該改進裝置提高了實驗的準確性和自動化程度，作為原實驗方法的有益補充,可應用于大學基礎物理實驗及課堂演示教學環節，也可應用于聲波近場區傳播規律的研究.

虛擬儀器；單片機；自動控制；聲速測量；振幅法

1　為什么要改進振幅法測量聲速實驗

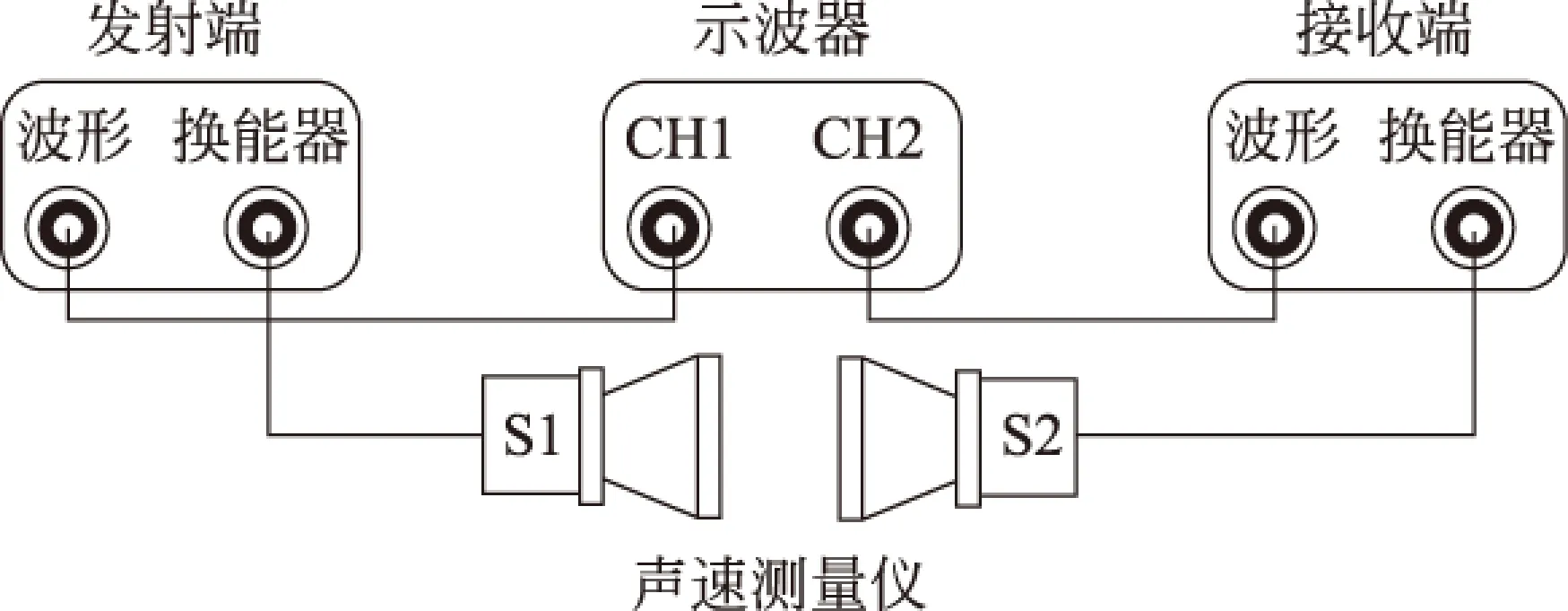
圖1　振幅法測量聲速裝置

振幅法測量聲速實驗是大學物理實驗中一個重要內容.振幅法的實驗裝置如圖1所示[1]，S1端面發出平面聲波向S2傳播，經S2反射之后在兩端面之間形成駐波場.場中任意兩個信號幅度極大值之間的距離即為該聲信號的半波長λ/ 2[2].因此，只要測出信號幅度達到極大時的各位置點，便可以利用下式求出聲速v

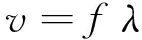
(1)

式中,v為聲速(m/s)；f為聲波頻率(Hz)；λ為聲波波長(m).

然而，在實驗操作過程中該方法存在明顯不足：首先，振幅極大值的位置依靠目測判斷，而波形在極值附近的變化并不明顯，這就會產生由于主觀因素和示波器的分辨率限制而引入的誤差.另外，端面之間的距離通過目視標尺刻度得到，不能得到精確結果[3].為此，本文在振幅法的基礎上，對實驗儀器進行改進，通過極值點檢測算法，設計出基于單片機的聲速測量綜合實驗系統，彌補了原系統存在的上述缺點，提高了測量的準確度，也為教師的課堂實驗演示提供了便利.

2　系統設計

針對刻度讀取不準確的問題，本文將步進電機與聲速測量儀相連，控制端面勻速移動，以步進電機轉過的步數間接表示接收端面S2的位移；由單片機控制模數轉換器ADC0809對接收端S2的信號進行采集，然后通過RS232串口上傳到PC機，進而由軟件自動判斷極值位置，為準確測量提供可能[4,5].

該系統以單片機為核心，如圖2所示.

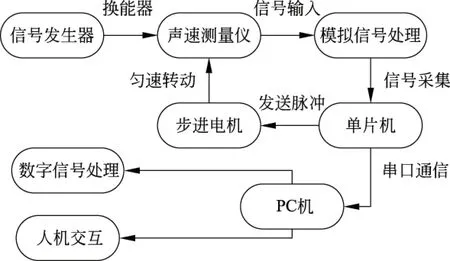
圖2　系統框圖

首先通過信號采集電路對接收端的模擬信號進行整流、濾波、放大等預處理.該電路以AD737芯片為核心.接收到信號首先經過高通濾波器，濾除低頻干擾信號，使頻率較高的有效信號輸入到下一級.AD737芯片將交流信號轉換為與振幅線性相關的直流信號，并使放大后的信號經分壓電路轉換為0～5V以滿足單片機采樣的要求.

單片機通過模數轉換器ADC0809采集直流信號，得到對應交流信號的相對幅度，同時均勻地發送脈沖信號，控制步進電機勻速轉動，帶動由電機驅動的聲速測量儀轉盤轉動，保證了發射端和接收端勻速靠近或遠離，再利用串口通信將數據實時地上傳到PC機.

PC機接收到數據后，在人機交互界面上實時顯示接收信號幅值隨S2移動而變化的趨勢，并采用中值濾波、快速傅里葉變換等算法進行數據處理，得到各極值的位置后通過線性回歸計算半波長λ/2，進而由波長求得聲速.

3　算法實現

3.1原理概述

實驗過程中，接收端的電壓值x(l)是其位置l的連續函數.為方便測量和計算機處理，本實驗將其離散化，即步進電機每轉動一步，單片機即發送一組數據到PC機，因此總測量次數等于轉動步數N，設第n次測量所得電壓值為x，則實驗結束后可得長度為N的離散序列x[n].在電機勻速轉動的前提下，接收器位移與轉動步數成正比，即：

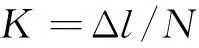
(2)

式中,Δl為接收器位移(m)；N為電機轉動步數，K為比例系數.

根據振幅法原理，諧振位置對應交流信號振幅的極大值，變換后的直流信號會出現相應峰值，其間距為半波長λ/2.若能在離散域中計算出相鄰峰值間的測量次數Δn，即可根據比例關系求得連續域中的半波長為

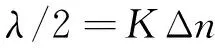
(3)

聲速v可由公式(1)、(2)、(3)聯立得

v=2fΔnΔl/N

(4)

以上各物理量中，f可由信號源讀取，Δl可通過讀取聲速測量儀的標尺得到，因此處理算法的關鍵在于求得離散域中相鄰峰值間的測量次數Δn.

3.2中值濾波

為減小噪聲干擾，首先對數據序列進行數字濾波.綜合考慮濾波效果和算法復雜度，本系統采用中值濾波算法，即對每個數據點，以該點為中心把前后m個數據排序，得到[d0，d1，…，dm-1]，用中位數(即dm/2)來代替原數據.適當選擇m值，既保證濾波后的數據能反映原信號的變化趨勢，又能有效防止尖峰脈沖的干擾.

3.3快速傅里葉變換

在信號序列中，不僅諧振位置存在明顯的峰值，其他位置亦可能由于擾動而出現局部極大值，因而不能直接檢測峰值點以判斷諧振位置.考慮到離散序列x[n]中峰值點的分布具有周期性，故引入離散傅里葉變換，將x[n]分解為若干單一的諧波分量，以獲得各諧波的幅度和相位信息[6].為提高計算效率，系統采用以2為基底的快速傅里葉變換(FFT).變換后的離散頻域序列X[k]的幅頻曲線中會出現明顯的峰值，如圖3所示.

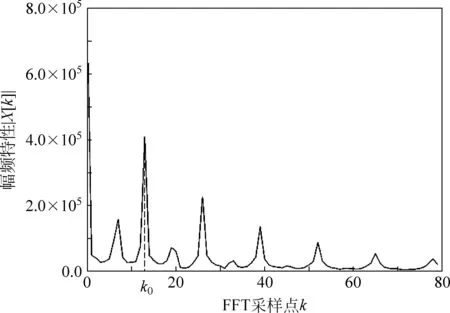
圖3　諧振位置檢測

除直流分量外的最大峰值對應的橫坐標k0代表基頻，即離散序列中峰值點的個數，據此求得Δn的估計值為

(5)

考慮到聲速測量儀長度有限，峰值點數目k0一般不超過40個且只能取整數，若單純采用FFT則精度受限.但作為預測量步驟，FFT可為精確測量Δn提供依據，在本系統中仍有存在的必要.

3.4諧振位置檢測與線性回歸

在FFT的基礎上，確定出每個諧振位置對應的峰值點，如圖4.創建數組top，首先按照估測周期Δn′，選取一個周期內最大值在時間軸上的對應值，作為第0個峰值點top[0]，其后的第i個峰值點為top[i] (i=1,2,3，…)，則相鄰的top[i]與top[i-1]的差約為Δn′，即top[i]=top[i-1] +Δn′,但由于Δn′為近似值，可認為top[i]存在于top[i-1] + 0.9Δn′和top[i-1] + 1.1Δn′之間，將此范圍中電壓最大值的位置確定為top[i].以此類推，即可求得所有諧振位置.

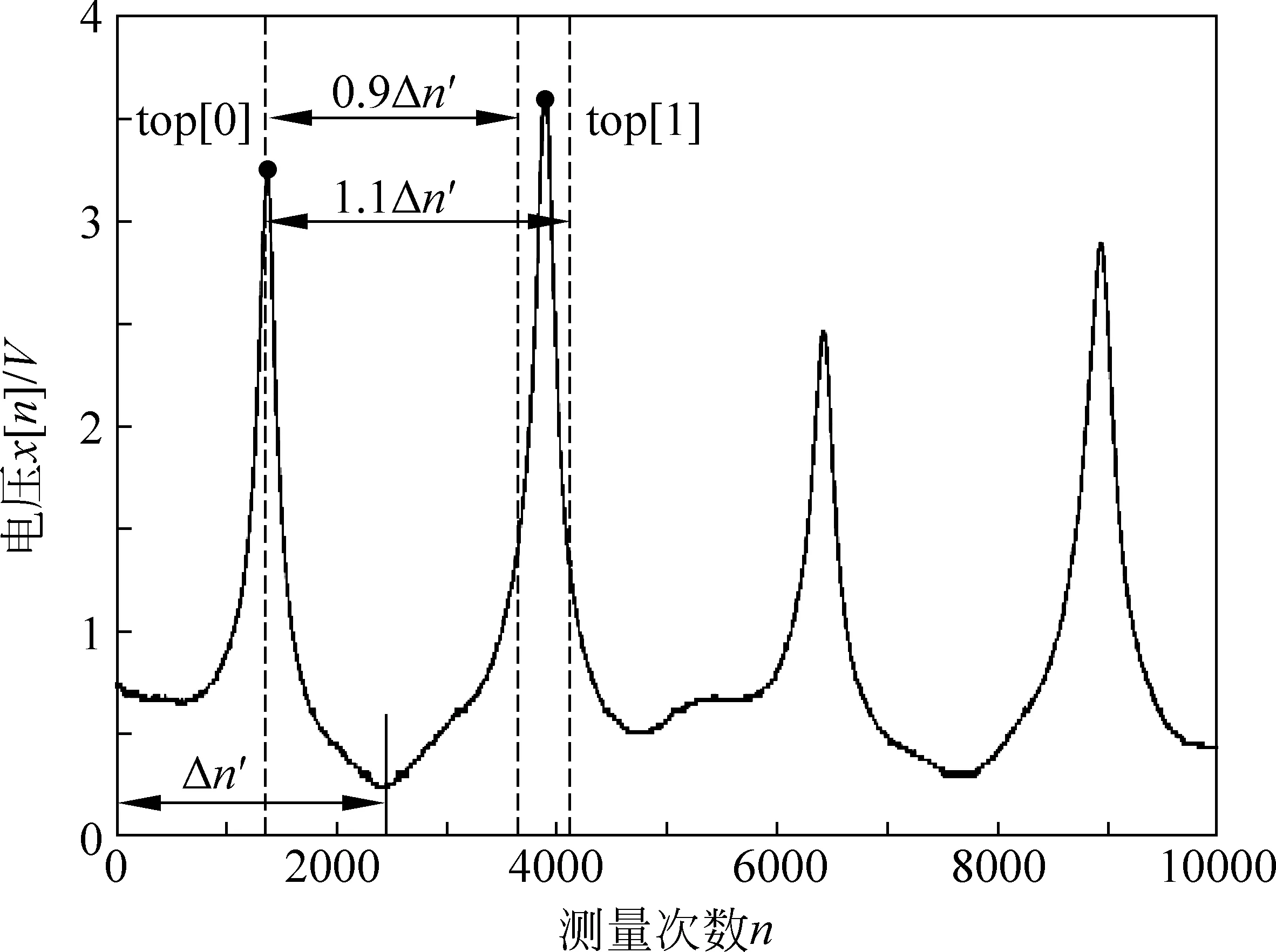
圖4　快速傅里葉變換

數組top[0],top[1],…,top[i],…中相鄰兩項的差應為相鄰峰值間的測量次數Δn.受隨機因素影響，差值并非嚴格相等，因此引入一元線性回歸進行擬合，從而以較高的精度計算出Δn值.

4　實驗結果

以某次實驗為例進行以下分析：

總測量次數N=32768，信號源頻率f=35.616kHz，實驗過程中接收器位移Δl=64.315mm，測得的諧振位置如表1：

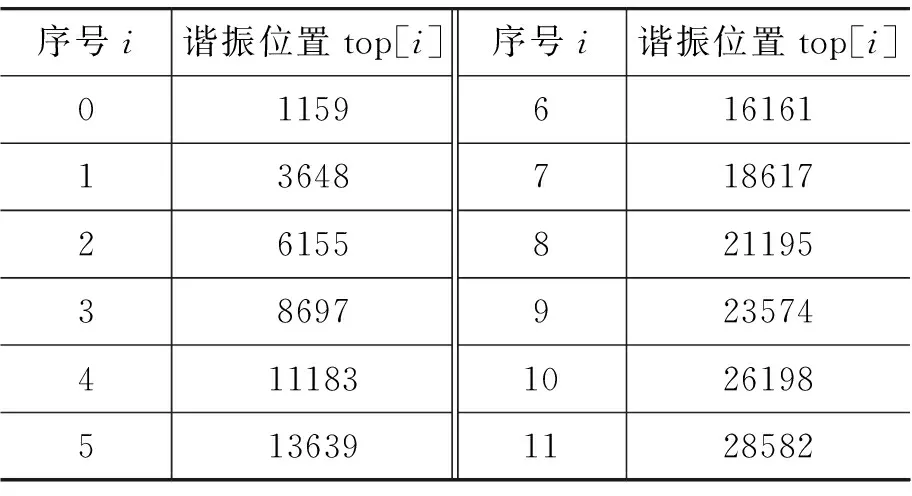
表1　諧振位置檢測

經線性回歸可得相鄰諧振位置間距Δn′=2496.01，代入式(4)中求得聲速為

v=2fΔnΔl/N=348.970(m/s)

(6)

實驗過程中傳感器測得的平均溫度為27.77℃，代入空氣中的聲速公式

vs=331.45(1+t/273.15)1/2m/s

(7)

求得理論值vs=347.891m/s，相對誤差η=0.31%.

按上述方法進行多次測試，結果如表2.

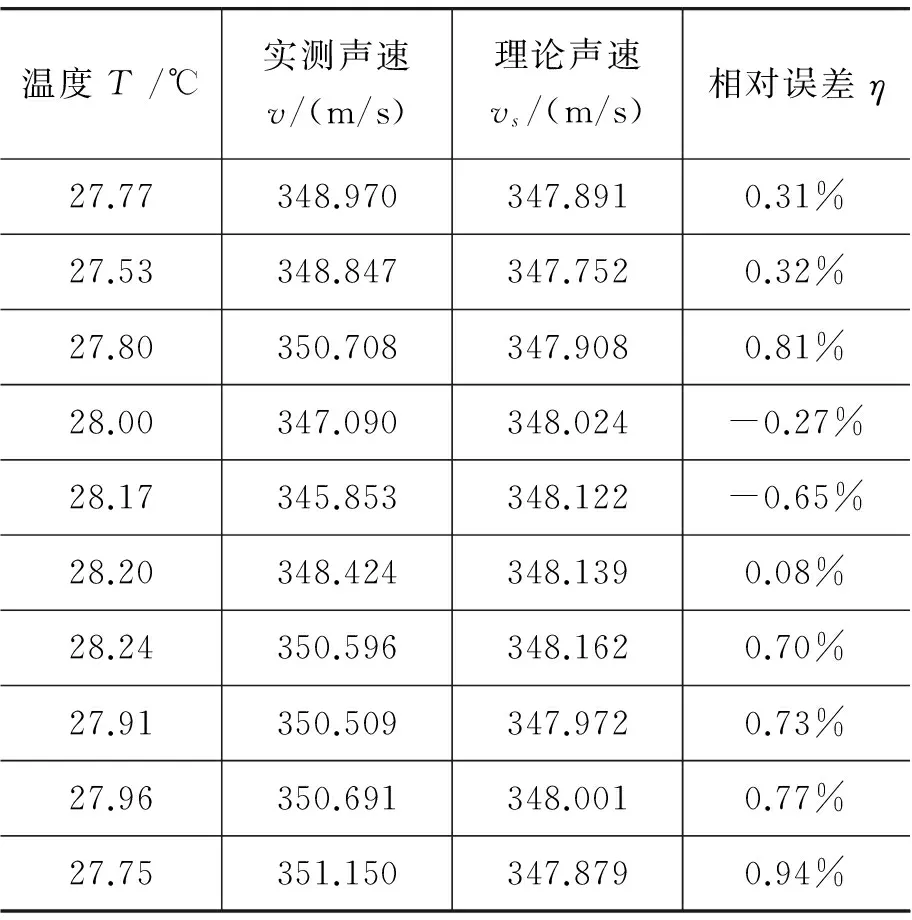
表2　系統測試結果

本系統在實驗原理、硬件結構和軟件算法方面均采取了減小誤差的措施.由實驗數據得，各組誤差均不超過1%，處于合理的范圍，可見本系統具有較高的準確度.誤差來源可能包括[7]：

(1) 信號源穩定性有限，實驗過程中頻率f存在細微的變化；

(2) 步進電機非嚴格勻速造成所測Δn的誤差；

(3) 刻度尺讀數造成Δl的誤差；

(4) 溫度傳感器精度有限，測得的溫度與環境溫度存在偏差使計算的理論真值存在偏差；

(5) 信號采集和處理電路存在微小噪聲；

(6) 受實驗條件和儀器限制，測量數據有限.

分析多次實驗過程，超聲波信號源頻率f一般為35～40kHz，頻率波動在20Hz以內，其誤差不超過0.06%；刻度尺最小分度0.01mm，Δl誤差不超過0.02%；測定若干次步進電機轉速，可得由電機不嚴格勻速造成Δn誤差在0.8%以內；由于諧振位置處電壓存在明顯的峰值，電路中的微小噪聲不會對Δn產生明顯影響；單片機所使用的12位溫度傳感器DS18B20最大測溫誤差為1℃，代入聲速公式求得的理論真值的最大偏差為0.17%，可認為求得的理論真值比較準確.綜上所述，本實驗的誤差主要來源于誤差項(2)，聲速v的相對誤差不超過1%，與實驗結果基本相符.

5　結論

與傳統實驗方法相比，改進后的實驗具有以下特點：

(1) 實現自動測量與計算，減少人工干預；

(2) 引入快速傅里葉變換和中值濾波等數字信號處理算法，減小噪聲干擾；

(3) 在PC機上實時顯示信號與換能器間距的關系曲線，直觀形象；

(4) 無需借助示波器，降低對實驗設備的要求，節約成本.

該聲速測量實驗裝置可應用在大學基礎物理實驗及課堂演示教學環節，配合啟發式理論講解，使學生對聲速測量的原理和過程獲得更直觀的認識.也可應用于聲波近場區傳播規律的研究，以獲得聲波傳播過程的衰減特性數據.在信號采集、測量與數據處理方面，本平臺體現了“虛擬儀器”的設計思想.利用模塊化硬件和靈活的軟件算法代替實體儀器，具有易于開發和調試的優點，并兼備自動測量與演示功能，體現了儀器儀表領域的發展方向[8].

[1]李朝榮. 基礎物理實驗[M]. 修訂版. 北京: 北京航空航天大學出版社, 2013.

[2]康永剛,張秀娥. 對駐波法測聲速的討論[J]. 物理通報，2011(11): 11-12.

[3]劉興俊,王昆林. 超聲波聲速測定的三種實驗方法比較研究[J]. 實驗科學與技術，2011, 9 (2): 184-187.

[4]朱方璽,曹偉然. 聲速測量實驗儀的改進[J]. 物理實驗，2011, 31 (10): 40-43.

[5]張俊玲.聲速測量演示實驗的設計與實現[J]. 實驗科學與技術，2012, 10 (4): 14-16

[6]程佩清.數字信號處理[M].4版.北京: 清華大學出版社, 2013.

[7]陳中鈞.超聲波聲速測量試驗中的誤差分析[J].實驗科學與技術，2005(10): 146-147.

[8]秦樹人，尹愛軍，劉小峰.現代虛擬儀器[M].北京: 機械工業出版社, 2011.

■

IMPROVEMENT OF SOUND VELOCITY MEASUREMENT METHOD

Li Tianyi1He Wozhou1Lu Zixuan2Chen Yan3Li Hua3

(1School of Electronic and Information Engineering, Beihang University, Beijing 100191;2The Affiliated High School of Beijing People’s Congress, Beijing 100191;3School of Physics and Nuclear Energy Engineering, Beihang University, Beijing 100191)

According to the design principle of virtual instruments, a sound velocity measurement system based on microcontroller unit is realized, which compensates for some problems of the original experiment with amplitude approach. In this system, the microcontroller unit samples the received signals and controls the uniform motion of the receiver. The data array is uploaded to the personal computer (PC), which is firstly processed with median filtering, followed by the fast Fourier transform. Then the more precise detection of extreme points and linear regression for further correction are implemented. In contrast to the manual operation, the system improves the accuracy of the measurement with good effects of human-computer interaction, which complements the original experiment and teaching demonstration, and also can be applied to research on the laws of the acoustic near-zone spread.

virtual instrument; microcontroller unit; automatic control; sound velocity measurement; amplitude method

2015-10-23;

2016-03-22

李天一，男，北京航空航天大學在讀本科生.

陳彥，男，實驗師 ，主要從事物理實驗教學與管理工作，研究方向為測試計量技術及儀器.chenyan@buaa.edu.cn

引文格式: 李天一,何沃洲,盧子璇,等. 聲速測量實驗方法的改進[J]. 物理與工程，2016，26(3)：29-32.