有限長周期參數梁的動力學特性

張　巍，應祖光

（1.浙江理工大學 經濟管理學院實驗中心，杭州 310018；2.浙江大學 航空航天學院力學系，杭州 310027）

?

有限長周期參數梁的動力學特性

張巍1，應祖光2

（1.浙江理工大學 經濟管理學院實驗中心，杭州 310018；2.浙江大學 航空航天學院力學系，杭州 310027）

研究有限長周期參數梁的動力學特性。建立周期參數梁的運動微分方程，得到梁高度周期性的參變方程，運用伽遼金法轉化為多自由度狀態方程，然后得到周期參數梁的固有頻率方程。最后通過數值結果說明梁位移展開項數對于固有頻率與動力學特性的影響，特別是周期參數為低周期或高頻率情況時，固有頻率隨周期參數頻率與幅度的變化及頻帶間隙（固有頻率隨周期參數頻率變化的空隙）的退化與梁彎曲波的彌散等。

振動與波；動力學特性；有限長梁；周期參數

周期結構具有特殊的動力學性質，例如波動空間或振動模態的局部化，它對于結構動力學特性的優化具有重要作用。90年代前后，關于周期結構的動力學特性進行了廣泛研究，主要工作集中于無限尺寸周期結構的周期波動特性（包括特征波數與頻率），它基于一個周期單元結構受兩端周期性約束的特性分析，周期性導致特征頻率的帶隙，即“band gap”［1-6］。然而，實際工程結構的尺寸是有限的，邊界約束使結構固有頻率離散化，而且低階固有模態的空間分布是跨越整個結構的（該模態不具有周期性），因此有限尺寸周期參數結構的動力學特性將不同于上述周期結構［7］。此外，由彈性動力學理論［8］知梁與板等結構的彎曲波具有彌散性（不能保持周期性），其動力學特性不同于傳統的達朗貝爾波（例如弦與桿的波）。而高頻波的波長短，空間離散分析時需要劃分足夠細單元或考慮足夠多高階模態，否則將導致偽特性。關于這些有限尺寸周期參數結構的動力學特性尚需進一步研究。

文中將研究有限長周期參數梁的動力學特性。先建立周期參數梁的運動微分方程，考慮梁高度的周期性得到參變方程；再用空間諧波函數離散梁位移，按伽遼金法推導梁的多自由度狀態方程，進一步得到固有頻率方程；最后通過數值結果說明梁位移展開項數對于固有頻率的影響，特別是周期參數為低周期或高頻率情況下的影響，固有頻率隨周期參數頻率與幅度的變化，頻帶間隙（固有頻率隨周期參數頻率變化的空隙）的退化，及彎曲波的彌散（特征頻率與波數的非線性關系，導致波隨傳播而變形）等。

1　有限長周期參數梁的動力學方程

考慮具有周期參數的有限長水平簡支梁（圖1），按照歐拉-伯努利模型，其運動微分方程為

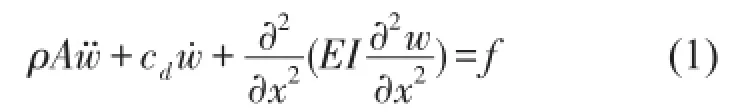
式中w是垂直位移，x是水平坐標，f是激勵，ρ是質量密度，E是彈性模量，A是橫截面面積，I是慣性矩，cd是阻尼系數。其中，ρA與EI是x的周期（T0）函數。展開式（1）的偏導數項得

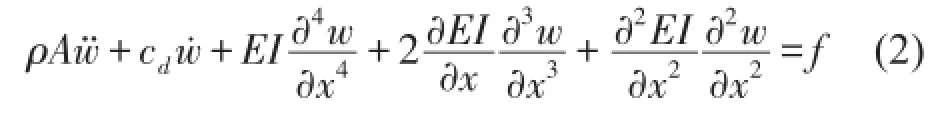
對位移與坐標無量綱化，式（2）成為

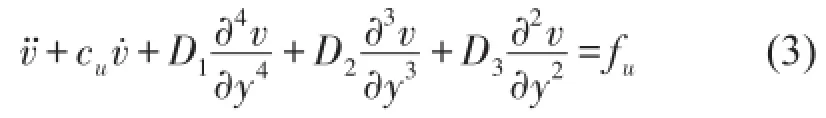
式中ν是無量綱位移，坐標y=x/L，L是梁長度，對于高h寬b的矩形截面梁，系數D1、D2、D3分別為

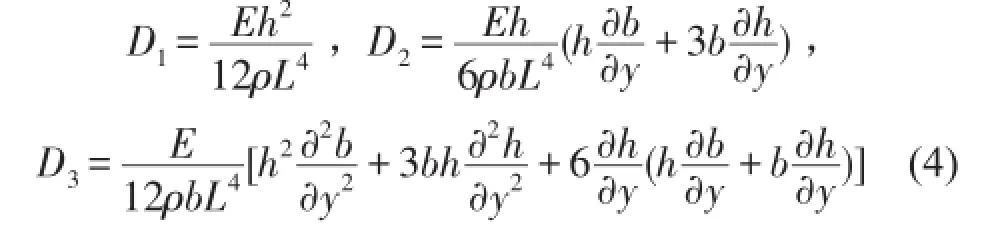
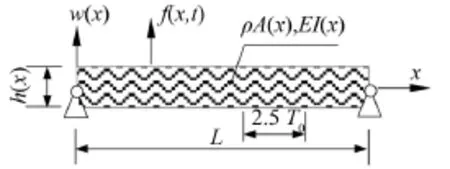
圖1　有限長周期參數簡支梁

若考慮周期變化的高度h=h0（1+λssinωhy），其中h0是平均高度，λs是周期高度比或周期參數幅度，ωh（2πL/T0）是周期參數變化頻率。則系數D1、D2、D3是式（3）的周期參數，導致空間參變，成為非線性問題。簡支梁的邊界條件為

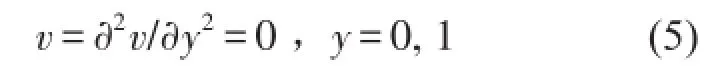
式（3）與式（5）組成有限長周期參數簡支梁的基本方程，邊界約束使固有頻率離散化，而參數周期性又將改變其動力學特性。

2　空間展開與特征值解

空間離散化是解上述問題的有效分析方法，但參數周期性將使各個分量相互耦合，從而導致高階分量對低階分量產生影響，特別是周期參數變化頻率較高時，需要考慮足夠的高階分量。梁無量綱位移可展開為

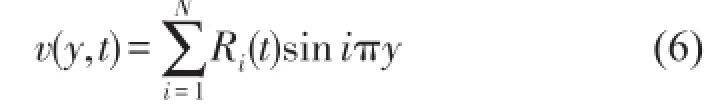
式中Ri是時間函數，N是項數。將式（6）代入式（3），按伽遼金法得多自由度系統方程

式中廣義位移向量R=［R1，R2，…，RN］T，Cu是阻尼陣，Ku是剛度陣，Fu是激勵向量，其中元素

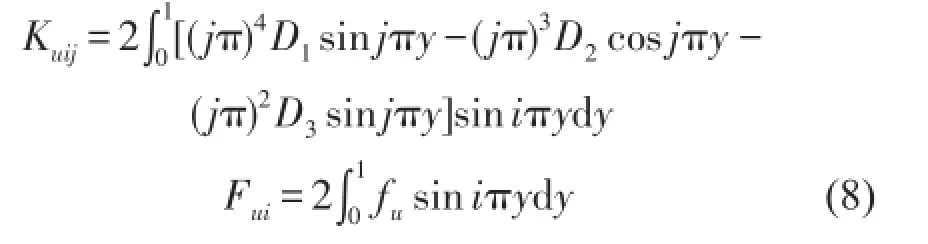
式（7）可表示為狀態方程

式中

周期參數與展開模態的耦合作用在剛度Ku中，因此參數周期性通過調制系統剛度改變動力學特性及響應。由式（9）解得狀態向量，代入式（6）即得梁位移。而系數陣A的特征值確定了梁固有頻率，固有頻率即為特征值的正的虛部。由此可分析參數周期性對于固有頻率的調制與影響。

3　數值結果

設周期性梁的基本參數ωh=10p，λs=0.2，N= 50，模態阻尼比ζ=0.005，無量綱化頻率常數ω0=p2（h0/L2）（E/12ρ）1/2（除了圖2的指定值）。由系數陣A計算固有頻率（用MATLAB函數），式（9）與式（6）用龍格-庫塔法計算響應，結果如圖2—圖5所示。圖2表明周期性梁位移展開項數N對前8階固有頻率的影響，當N350時結果才收斂，否則將導致偽特性。

圖3展示前4階固有頻率隨周期參數頻率（ωh/ p）的變化，參數變化頻率對高階固有頻率的影響較大，低參數頻率時影響較顯著，各階固有頻率隨參數頻率增加而降低，可跨越低參數頻率時的低階固有頻率，即頻帶間隙（固有頻率隨周期參數頻率變化的空隙）退化。

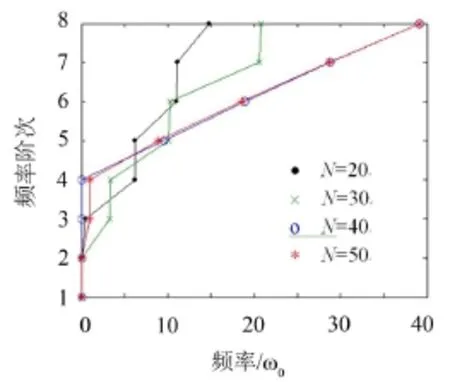
圖2　固有頻率隨項數（N）的變化（ωh=20π，λs=0.3）

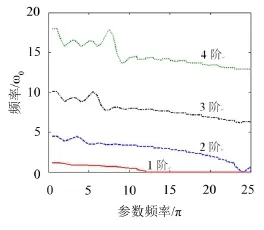
圖3　固有頻率隨參數頻率（ωh）的變化

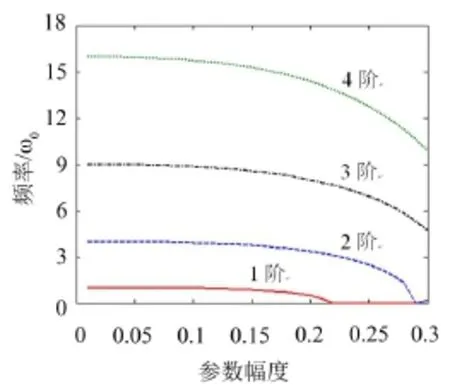
圖4　固有頻率隨參數幅度（λS）的變化

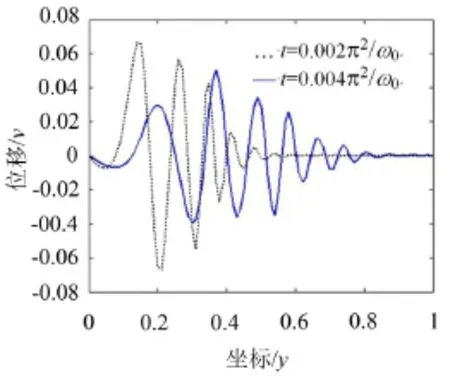
圖5　彎曲波的彌散

圖4展示前4階固有頻率隨周期參數幅度λs的變化，各階固有頻率隨參數幅度增加而降低，可跨越低參數幅度時的低階固有頻率。

圖5展示梁在左端附近初始單位脈沖波（寬Dy= 0.01）作用下兩個時刻的響應，波往右端傳播時幅度降低、寬度增大，即為波的彌散。因此，不存在理想的單頻波或達朗貝爾波［8］。

4　結語

研究了有限長周期參數梁的動力學特性，建立周期參數梁的運動微分方程，得到梁高度周期性的參變方程，并按伽遼金法進一步得到多自由度狀態方程，及固有頻率方程。數值結果表明，位移展開項數對于梁固有頻率與動力學特性有重要影響，特別是周期參數為低周期或高頻率情況時，固有頻率隨周期參數頻率與幅度增加而降低，超過一定界限時頻帶間隙（固有頻率隨周期參數頻率變化的空隙）將退化，梁彎曲波具有彌散性。

［1］MEAD D J.Wave propagation in continuous periodic structures:researchcontributionsfromSouthampton，1964-1995［J］.Journal of Sound and Vibration，1996，190:495-524.

［2］BENDISEN O O.Localization phenomena in structural dynamics［J］.Chaos，Solitons and Fractals，2000，11: 1621-1660.

［3］ROMEO F，LUONGO A.Vibration reduction in piecewise bi-coupled periodic structures［J］.Journal of Sound and Vibration，2003，268:601-615.

［4］RAGHAVAN L，PHANI A S.Local resonance bandgaps in periodic media:theory and experiment［J］.Journal of the Acoustical Society ofAmerica，2013，134:1950-1959.

［5］程世祥，張志誼，華宏星.周期桁架結構浮閥隔振特性分析與實驗研究［J］.噪聲與振動控制，2011，31（6）：5-9.

［6］陳斌，黃修長.周期結構振動控制研究現狀［J］.噪聲與振動控制，2011，31（5）：37-41.

［7］ HVATOV A，SOROKIN S.Free vibration of finite periodic structures in pass-and stop-bands of the counterpart infinite waveguides［J］.Journal of Sound and Vibration，2015，347:200-217.

［8］ MIKLOWITZ J.The theory of elastic waves and waveguides［M］.New York:Elsevier North-Holland，1978.

Dynamic Characteristics of Finite-length Periodic Parameter Beams

ZHANG Wei1，YING Zu-guang2

（1.Laboratory Center，School of Economics and Management，Zhejiang Sci-Tech University，Hangzhou 310018，China；
2.Department of Mechanics，School ofAeronautics andAstronautics，Zhejiang University，Hangzhou 310027，China）

The dynamic characteristics of finite-length periodic parameter beams are studied.The differential equation of motion of the periodic parameter beams is presented，and the partial differential equation with spatial varying parameters for the periodic-height beam is obtained.Then，the equation is converted into a multi-DOF state equation using Galerkin method，and a set of algebraic equations for natural frequencies of the periodic beam is obtained.Numerical results are given.The influence of the number of series expansion terms of the displacement on the natural frequencies and dynamic characteristics of the beam is analyzed.Variation of the natural frequencies with the change of the frequency and amplitude of the periodic parameter，degeneration of the band gaps among the natural frequencies，and the bending waves scattering are analyzed in the case of large periodic parameter frequencies.

vibration and wave；dynamic characteristics；finite-length beam；periodic parameter

O32；TB53

ADOI編碼：10.3969/j.issn.1006-1335.2016.04.005

1006-1355（2016）04-0024-03

2016-01-13

國家自然科學基金資助項目（11572279）；浙江省自然科學基金資助項目（LY15A020001）

張巍（1965-），女，江蘇南通人，高級工程師，學士，主要從事信息系統與控制研究。E-mail:zhweihz@zstu.edu.cn