ASAC系統中少測點條件下的近場聲壓誤差傳感策略

蘇常偉，朱海潮，毛榮富，蘇俊博

（1.海軍工程大學 振動與噪聲研究所，武漢 430033；2.船舶振動噪聲重點實驗室，武漢 430033）

?

振動理論與數值解法

ASAC系統中少測點條件下的近場聲壓誤差傳感策略

蘇常偉1，2，朱海潮1，2，毛榮富1，2，蘇俊博1，2

（1.海軍工程大學 振動與噪聲研究所，武漢 430033；2.船舶振動噪聲重點實驗室，武漢 430033）

根據有源控制策略設計簡潔、有效的誤差傳感非常關鍵。針對基于聲壓聲輻射模態的有源控制策略，具體設計與之對應的少測點條件下近場聲壓誤差傳感策略。首先，通過分析聲壓聲輻射模態的空間濾波特性，證明基于聲壓聲輻射模態的有源控制策略可行；然后，利用近場測量面上有限個測點的聲壓分布，通過求解模態展開所構成的欠定方程組的最小模最小二乘解，獲取前K階聲壓聲輻射模態伴隨系數的近似值，從而形成與基于聲壓聲輻射模態的有源控制策略相對應的近場聲壓誤差傳感策略；最后，以置于無限大障板上的鋼質簡支薄板為例，進行數值仿真分析。結果表明設計的誤差傳感策略可行，所獲得的前K階聲壓聲輻射模態伴隨系數具有較高的精度。

聲學；誤差傳感；近場聲壓；聲壓聲輻射模態；有源結構聲控制；少測點

近年來，為了有效控制振動結構低頻輻射噪聲，有源結構聲控制（Active structural acoustic control，ASAC）技術受到了人們廣泛關注。在ASAC系統中，根據有源控制策略設計簡潔、有效的誤差傳感非常關鍵。所謂誤差傳感策略，是指在控制系統中獲取誤差信號的方法和手段。良好的誤差傳感策略既可采集到對輻射聲功率起主要作用的信息，有效實施有源控制策略，又可避免控制器處理過多輸入信息而導致運算能力下降［1］。傳統的ASAC系統采用位于遠場的聲學傳感器檢測聲學量（如場點聲壓）作為誤差信號，構成系統的目標函數，這在實際應用中受到一些限制，不僅難以獲得全局控制效果，而且會由于結構作動器和傳感器之間存在“時延”而導致控制效果不佳。

Borgiotti等學者在90年代初期提出聲輻射模態的概念，并指出聲輻射模態的重要特性：每階聲輻射模態單獨輻射聲功率［2］。由此，一種基于聲輻射模態的有源控制策略應運而生，即只要控制有限的幾階主導輻射模態的聲功率，就能有效地控制結構的低頻輻射噪聲，這使得有源結構聲控制的實現大為簡便。根據聲功率表達式中參量形式不同，聲輻射模態可分為振速聲輻射模態、聲壓聲輻射模態、源強（源強密度）聲輻射模態和力聲輻射模態等。目前，國內外學者普遍選用結構表面振速聲輻射模態進行該有源控制策略的研究，其對應的誤差傳感策略關鍵在于采集到對聲功率起主要貢獻的幾階主導振速聲輻射模態信息。已知梁、板等簡單結構在中、低頻時的主導輻射模態即為其前幾階聲輻射模態。TANAKA等使用聚偏氟乙烯（Polyvinylidene fluoride，PVDF）壓電傳感器測量簡支板的振速聲輻射模態［3］。吳錦武、李雙等則對利用PVDF壓電薄膜測量平板結構前幾階振速聲輻射模態伴隨系數進行了深入研究［4-5］。然而，雖然通過設計PVDF壓電薄膜形狀可以測量聲輻射模態伴隨系數，但要同時獲得前幾階聲輻射模態伴隨系數所需要的PVDF薄膜個數非常多，階次越高薄膜形狀越復雜，且PVDF傳感器的設計受到振動結構邊界條件的限制，這會在實際應用中帶來不便。吳錦武、姜哲等提出可在振動結構上測量有限個點的振動速度分布，通過求解欠定方程組得到前幾階振速聲輻射模態伴隨系數近似值，這種直接測量結構表面振速的方法在實驗中較為常用［6］。然而，對于一些對安裝傳感器比較敏感的振動結構，該方法便不再適用，比如：

（1）非常薄的振動結構（比如薄板、薄殼等），它們對外界附加質量非常敏感，測點陣列的安裝不可避免地會改變其振速場，從而導致有源控制策略無法有效實施；

（2）在實際應用中，在一些結構表面布置傳感器陣列存在極大困難，同時布置位置也會受到各種條件的限制。

陳克安等為了解決有源聲學結構中誤差信息的傳感問題，推導了基于近場聲壓的輻射聲功率計算公式，指出利用近場聲壓作為誤差信息可以實現結構聲輻射的有源控制［7］。這就為安裝傳感器陣列比較敏感的振動結構提供了一個可行的誤差傳感途徑。然而，對于如何利用近場聲壓數據具體設計可以獲得全局控制效果、易于工程實現且適用于敏感結構的誤差傳感策略，文獻［7］并沒有開展具體研究及驗證。本文從聲壓聲輻射模態出發，具體設計了一種少測點條件下的近場聲壓誤差傳感策略，并對其有效性和可行性進行數值仿真驗證，后續研究中還將開展測點布置優化研究以實現更少測點、更高精度。

1　基于聲壓聲輻射模態的有源控制策略

目前，國內外學者對振速聲輻射模態進行了全面且深入的研究，而對聲壓聲輻射模態的研究還比較少。本文首先討論聲壓聲輻射模態的空間濾波特性，論證基于聲壓聲輻射模態的有源控制策略是否可行。

和振速聲輻射模態的求解方法類似，文獻［8］給出了聲壓聲輻射模態的基本算法，這里不再贅述。振動結構表面的聲壓可以表示為各階聲壓聲輻射模態疊加的形式

其中P為結構離散后由表面聲壓組成的N維列向量；Φ為N×N維矩陣，其列向量φi為結構的聲壓聲輻射模態，模態之間相互正交；ci=φiTP為第i階聲壓聲輻射模態伴隨系數，c為由ci組成的N維列向量；N為離散單元數目。

振動結構的輻射聲功率可寫為

其中λi（i=1，2，…N）為每階聲壓聲輻射模態對應的特征值，從物理意義上講，λi與各階模態的聲輻射效率成正比。

接下來建立聲壓聲輻射模態頻域和空間波數域的聯系，用于分析聲壓聲輻射模態的空間濾波特性。以一置于無限障板上的正方形簡支平板為例，取邊長L=0.5 m。將平板離散為25×25個等面積單元，圖1為平板在頻率為380 Hz時的前6階聲壓聲輻射模態，圖2給出了圖1中平板的前六階聲壓聲輻射模態對應的波數域譜。由圖2可見，此頻率下傳播波成分主要集中在前幾階模態中。分析低頻其它頻率，可得到相同結論。因此，在低頻時平板的聲壓聲輻射模態具有明顯的空間濾波特性，即前幾階聲壓聲輻射模態輻射的聲功率占結構總聲功率的絕大部分。由此可得，控制前幾階聲壓聲輻射模態即可有效控制結構的遠場聲輻射，即基于聲壓聲輻射模態的有源控制策略是可行的。

圖1　平板前6階聲壓聲輻射模態

圖2　平板前6階聲壓聲輻射模態對應波數域譜

2　誤差傳感策略

根據式（2）可知，基于聲壓聲輻射模態的有源控制策略就是要通過控制使前K階聲壓聲輻射模態輻射的聲功率最小化，即ci→0，i=1，2，…，K。那么，與之相對應的誤差傳感策略應能夠提供前幾階聲壓聲輻射模態的伴隨系數信息。分析式（1），可以發現利用結構表面聲壓分布求解模態伴隨系數需首先解決兩個問題：（1）實際應用中只能測量近場聲壓；（2）實際應用中很難獲得結構表面所有的聲壓分布。文獻［9］對問題（1）進行了研究，并得到結論：只要測量面與源面間距遠小于聲波波長，則與源面等面積的測量面聲壓可以近似作為有源控制的誤差變量。基于此，針對問題（2）具體設計一種少測點條件下基于聲壓聲輻射模態的近場聲壓誤差傳感方法，來獲取前幾階聲壓聲輻射模態伴隨系數的近似值。

由聲壓聲輻射模態的空間濾波特性可知，式（1）的右端具有良好的收斂性。為簡化計算，可采用模態截斷的形式來表示（考慮頻率相關項ω），

其中M為模態截斷階數，M＜＜N；S為測量面面積，與源面面積相等。為了獲得前K階聲壓聲輻射模態的伴隨系數ci（i=1，2，…，K，K＜M ），我們在近場測量面上選取N1個測點xl，l=1，2，…，N1，在每一個測量點xl測量近場聲壓，記為Pl（xl，ω ）。聲壓向量中有N1個元素是已知的，將式（3）中包含這些元素的方程都抽取出來重新組成一組方程組，用矩陣和向量形式表示為

式中P'為N1個測點的聲壓值Pl（xl，ω）組成的向量；φi'為聲壓聲輻射模態向量φi中對應N1個測點所在單元的元素組成的向量；Φ'為M個向量φi'組成的矩陣，需要注意的是，這里不同向量φi'之間不再正交。

為實現少測點的目標，同時也為了保證誤差傳感的實時性，一般取N1＜M。這時，方程組（4）為欠定方程組，將存在無數組解，常規方法無法求得準確解，采用最小模最小二乘法求解方程組（4）的最佳逼近解，也稱最小模最小二乘解

3　誤差傳感策略對控制效果的影響

上一節中給出了基于聲壓聲輻射模態的近場聲壓誤差傳感策略，利用近場測量面少數點的聲壓分布即可得到前K階聲壓聲輻射模態伴隨系數的近似值。下面以聲功率降低量作為評價控制效果的指標，分析上述誤差傳感策略對控制效果的影響，從而驗證其可行性。

當模態截斷階數為M時，振動結構輻射聲功率可由式（2）改寫為

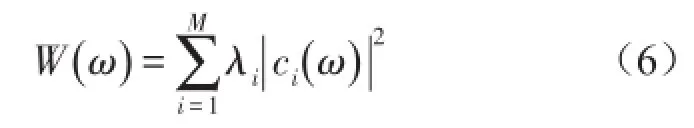
基于聲壓聲輻射模態的有源控制策略就是要通過控制使前幾階聲壓聲輻射模態伴隨系數變為零，即ci→0，i=1，2，3，4…。那么，控制后結構的聲功率為

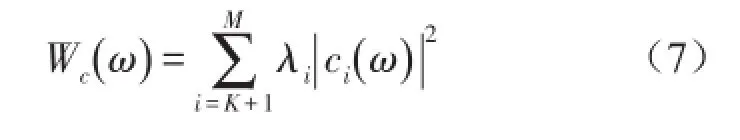
聲功率降低量為

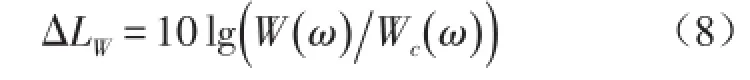
然而，當利用近似值c?i來代替ci時，控制目標變為使c?i→0，i=1，2，…，K，其控制后的聲功率為

這時，聲功率降低量為

比較ΔLW和ΔLW'，若兩者一致，就可以判定上述基于聲壓聲輻射模態的近場聲壓誤差傳感方法是可行的，可以作為基于聲壓聲輻射模態的ASAC系統中的誤差傳感策略。

4　數值仿真分析

以置于無限大障板上的鋼質簡支薄板為數值研究對象。以平板左下角頂點為坐標原點，建立正交坐標系。平板尺寸為L×B×h=0.5 m×0.5 m×0.008 m，彈性模量E=2×1011Pa，泊松比υ=0.28，材料密度 ρs=7 800 kg/m3，空氣中聲速 c0=343m/s。在平板上位置（0.125 m，0.125 m）處施加幅值為10 N的初始簡諧力Fp激勵平板產生聲場，頻率 f取100 Hz～800 Hz。

下面通過數值仿真驗證上述誤差傳感策略的有效性。將平板均勻離散為25×25個小面積單元，取測量面距離平板0.1 m，分別在測量面上均勻對稱地取3×3和5×5個測點，其位置分布如圖3所示。

利用上述誤差傳感策略，取模態截斷階數M=50，求解前K=4階聲壓聲輻射模態伴隨系數的近似值。根據式（1）得到前4階伴隨系數的理論值，將近似值與之進行比較，并進行無量綱化處理，結果如圖4、圖5所示。

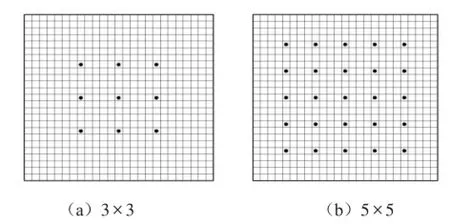
圖3　測量面上測點位置分布

從圖4、圖5中可以看出，由式（5）得到的前4階聲壓聲輻射模態伴隨系數的近似值與由式（1）得到的前4階伴隨系數的理論值大致吻合，尤其是第1、2、4階幾乎相等。增加測點數目，近似值與理論值更加接近。因此，利用該誤差傳感策略得到的聲壓聲輻射模態伴隨系數的近似值可以較好的替代理論值作為有源控制策略對應的誤差信號，也即文中提出的少測點條件下的近場聲壓誤差傳感策略是有效的。

圖4　測點數N1=3×3時前4階模態伴隨系數對比

圖5　測點數N1=5×5時前4階模態伴隨系數對比

另外，圖中第1、2、4階伴隨系數分別在150 Hz、380 Hz、600 Hz處出現峰值，又經計算可知，150 Hz、380 Hz、600 Hz分別為平板（1，1）階、（1，2）階、（2，2）階振動模態頻率，分析可以發現，平板以（1，1）階振動模態振動時，其對應的主導輻射模態是第1階；平板以（1，2）階振動模態振動時，其對應的主導輻射模態是第2階；平板以（2，2）階振動模態振動時，其對應的主導輻射模態是第4階。這一結論和李雙在文獻［10］中提出的結構振動模態和聲輻射模態的對應關系相符。

同時，驗證將上述誤差傳感策略用于基于聲壓聲輻射模態的有源結構聲控制時的可行性。基于式（5）設計的近場聲壓誤差傳感策略對有源控制效果的影響，可通過對比由式（8）和式（10）得到的聲功率降低量來衡量，如圖6所示，實線表示根據式（8）得到的聲功率降低量，即理論值；虛線表示根據式（10）得到的聲功率降低量，即近似值。從圖6中可知，當測點數N1=3×3時，基于式（5）設計的誤差傳感策略可以得到較好的控制效果，除300 Hz～570 Hz頻段內存在偏差外，其它頻率處與理想的控制效果基本一致；增加測點數至N1=5×5時，近似值與理論值吻合更好。這也就證明了利用式（5）得到前K階聲壓聲輻射模態伴隨系數近似值的方法，作為基于聲壓聲輻射模態的ASAC系統中的誤差傳感策略是可行的。

圖6　測點數N1分別為3×3、5×5時聲功率降低量比較

5　結語

針對基于聲壓聲輻射模態的有源控制策略，具體設計一種少測點條件下的近場聲壓誤差傳感策略，即中、低頻時，利用近場測量面上少數點的聲壓分布，通過式（5）求解前幾階聲壓聲輻射模態伴隨系數的近似值，將其作為誤差傳感信號實現有源控制，并以置于無限大障板上的鋼質簡支薄板為對象，進行了數值仿真分析。結果表明，利用上述誤差傳感策略獲得的前K階聲壓聲輻射模態伴隨系數具有較高的精度，且將其用于基于聲壓聲輻射模態的有源結構聲控制是可行的。

文中設計的少測點條件下近場聲壓誤差傳感策略既不受振動結構邊界條件的限制，也彌補了結構表面誤差傳感方法在對安裝傳感器比較敏感的振動結構上無法有效實施的缺陷。該策略只需要測量近場少數點的聲壓分布，簡潔，有效，易于工程實現。相比于遠場聲壓傳感，它能夠實現全局控制效果，同時也使得ASAC系統簡單、輕便，符合向集成式系統發展的趨勢。

［1］吳錦武，姜哲.基于聲輻射模態有源控制的誤差傳感器設計方法［J］.機械工程學報，2008，44（3）：189-194.

［2］聶永發.聲輻射模態理論及其應用研究［D］.武漢：海軍工程大學，2014.

［3］TANAKA N，SNYDER S D，HANSEN C H.Distributed parametermodalfilteringusingsmartsensors［J］. Transactions of ASME Journal of Vibration and Acoustic，1996，ll8:630-640.

［4］吳錦武，姜哲.通過PVDF傳感器測量振動板結構的聲輻射模態伴隨系數［J］.振動與沖擊，2005，24（4）：59-61.

［5］李雙，陳克安.PVDF聲輻射模態傳感器設計中的關鍵問題研究［J］.西北工業大學學報，2007，25（2）：295-300.

［6］吳錦武，姜哲.基于有限點振速分布設計誤差傳感策略［J］.振動與沖擊，2007，26（1）：87-90.

［7］CHEN KE-AN，YIN XUE-FEI.Active control of radiated soundusingnearfieldpressuresensing［J］.Chinese Journal ofAcoustics，2004，23（3）:193-203.

［8］ BERKHOFF A P.Sensor scheme design for active structural acoustic control［J］.J.Acoust.Soc.Am.，2000，108（3）:1037-1046.

［9］陳克安.自適應聲學結構聲壓誤差傳感策略［J］.振動工程學報，2004，17（3）：301-305.

［10］LI SHUANG，CHEN KE-AN.The relationship between acoustic modes and structural modes and its applications［J］.Chinese Journal ofAcoustics，2007，26（2）:158-167.

Near Field Pressure Error Sensing Strategy under Less Measurement Point Condition forASAC Systems

SU Chang-wei1，2，ZHU Hai-chao1，2，MAO Rong-fu1，2，SU Jun-bo1，2

（1.Institute of Noise and Vibration，Naval University of Engineering，Wuhan 430033，China；2.National Key Laboratory on Ship Vibration and Noise，Wuhan 430033，China）

It is very important to design a simple and effective error sensing system on the basis of active control strategy.In this paper，aiming at the active control strategy based on pressure acoustic radiation modes，an equivalent nearfield pressure error sensing strategy under less measurement point condition is designed in detail.First of all，by analyzing the spatial wave-filtering characteristics of the pressure acoustic radiation modes，the feasibility of the active control strategy based on the pressure acoustic radiation modes is proved.Then，by measuring the pressure distributions at a few measurement points in the near-field measurement surface and solving the underdetermined equations made of modal superposition，the approximate adjoint coefficients of the first K order radiation modes can be obtained.Thus，a near-field pressure error sensing method corresponding to the active control strategy based on the pressure acoustic radiation modes is developed.Finally，a simply supported steel plate in an infinitely large baffle is simulated as an example.The results show that the error sensing strategy proposed is feasible and the approximate adjoint coefficients of the first K order radiation modes are more precise.

acoustics；error sensing；near-field pressure；pressure acoustic radiation mode；active structural acoustic control；less measurement point

TB535

ADOI編碼：10.3969/j.issn.1006-1335.2016.04.001

1006-1355（2016）04-0001-06

2015-09-25

國家自然科學基金資助項目（51305452）

蘇常偉（1990-），男，山東省滕州市人，博士生，主要研究方向為振動與噪聲控制。E-mail:scwtz@163.com

朱海潮，男，博士生導師。E-mail:haiczhu@163.com