巴赫《賦格的藝術》中的組合對稱

許金昕（江漢大學 音樂學院，湖北 武漢 430056）

巴赫《賦格的藝術》中的組合對稱

許金昕
（江漢大學 音樂學院，湖北 武漢 430056）

音樂中的一切對稱都可以歸納為“平移、反射、旋轉”等三種基本形式所組成的“群”的組合排列，對于巴赫《賦格的藝術》中組合對稱的分析可以探知音樂最深層結構中所蘊含的數學思想和藝術理想。也讓我們對巴赫創作中的理性和科學客觀性有了新的認識。

組合對稱；巴赫；群

一、對稱的含義及對稱群

音樂結構有很多種，其中對稱是一個基本且核心的概念。這在錢仁康先生的大作《音樂語言中的對稱結構》①中有詳細描述分析，他將對稱的基本形式分為：平行、逆行、反行、逆反行。但對于組合對稱及組合對稱之間的關系沒有過多探討。本文即以此概念來對音樂文本巴赫《賦格的藝術》②進行分析，力圖以一個突破口找到音樂的一種基本結構及其變換形式。據研究，西方藝術中的“對稱（symmetry）”源于希臘詞根“sym”和“metria”，組成的意思是“同樣的尺寸”［1］3。對此，德國數學家外爾解釋說：“如果有一樣可以加工的東西，你加工后它如前一樣，那么這東西就是對稱?！边@是說，所謂對稱，乃是一可量度之物經過轉換之后仍保持不變。在其專著《對稱》一書中，他引同是數學家的伯努利墓志銘上的話：“我雖然變了，但卻和原來一樣”來說明對稱的性質［2］76。

現代數學、物理學意義上的對稱，其實指不變性。變形之中的不變，變量之中的恒定。對稱的基本形式其實很有限，在二維空間里，對稱無非三種形式：平移、反射、旋轉。平移，指向量移動后的疊合。反射，反射后的疊合。即我們常說的鏡像、左右手對稱。旋轉，指繞一個中心點旋轉某一角度后的疊合。

音樂雖被稱為時間的藝術，但其對稱形式也不例外。音樂中，平移（即錢文所說平行）包括前后（同聲部）、上下（異聲部）、交叉（異聲部易位）平移；反射，包括上下（即錢文所說反行）、左右（即錢文所說逆行）反射；旋轉（即錢文所說逆反行），因為五線譜的特殊表現方式，樂曲中的旋轉一般為180°，即曲式中常說的倒影逆行③。其實巴赫在《賦格的藝術》中自己指出的“正向、倒影”等，就是平移和反射。根據現代數學中群論的研究，遵守某種運算和置換規則的集，就構成一個群。而根據數學家克萊因定理，任何系統的所有對稱變換集總是形成一個群。

一個對稱群包含如下特點［3］112：

1.封閉性。任何兩個元素通過運算所得結果也是這個群中的元素。若A、B為群中元素，則A+B也是群中的元素。

2.結合律。結合三個有序元素時，可以任意結合其中兩個，結果不變。如A+B=B+A，（A+B）+C=A+（B+C）

我們將二維對稱的方式集合成一個群，以0表示組合對稱，相當于運算規則“+”，A表示平移，B表示反射，C表示旋轉，則有列表如下：

注：*因為譜子上的旋轉只能以180°進行，故C+C回到原點

下面我們以“對稱即不變性”的現代含義重新考察巴赫《賦格的藝術》中的組合對稱，對文本中最基本且恒定的結構進行描述，精確而簡潔地重構巴赫文本中的對稱結構，尋找到巴赫所說的“尋找，那么我們會找到”的所謂“萬物至理”④。

二、組合對稱

（一）平移+平移，A+A，平移有前后平移、上下平移、交叉平移。

三種單一形式又可以任意組合，包括：

1.前后平移+交叉平移，如對位曲6第62-63小節

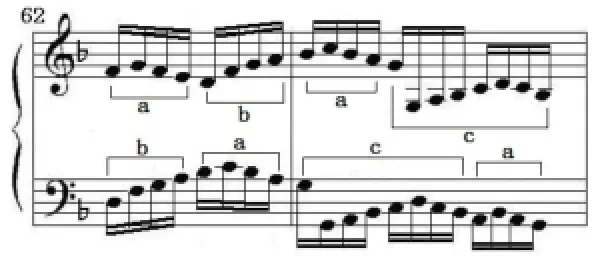
素材a在同一聲部內部整體地前后移動，即音樂曲式中常說的模進；同時，素材a-bac、bac-a又在不同聲部中上下交錯平移。譜面上看呈交叉形狀。

2.上下平移+前后平移，如對位曲9第1-15小節、第89-96小節

音樂素材在中（第1-8小節）高（第8-15小節）聲部上下平移，又在高聲部（第8-15小節、第89-96小節）前后平移。

3.上下平移+交叉平移，如對位曲7第21-22小節

素材a、b在高低聲部上下移動，素材c則在高低聲部中交叉移動。

（二）平移+反射，A+B，B+A，反射有上下反射（水平軸）和左右反射（縱軸）。

兩種反射和三種平移也可以任意組合，包括：

1.上下平移+左右反射。如對位曲12第45-47小節與對位曲12第51-53小節。素材abc和cba為左右反射，即曲式中常說的逆行。而素材b'又在高中上下平移。

2.上下平移+上下反射。如對位曲13高聲部第1-4小節素材與中聲部第5-8小節中的素材上下反射（水平軸），即曲式中常說的不同聲部的倒影，同時同一素材又上下平移至低聲部第9-12小節。形成高中、中低聲部上下反射，高低聲部上下平移。

3.交叉平移+上下反射。如對位曲8中聲部75-76小節與低聲部80-81小節、低聲部第77小節與中聲部82小節形成交叉平移，而低聲部84小節與中聲部85小節形成上下反射。

4.交叉平移+左右反射。如對位曲11第98-100、106-108小節。素材aab與baa為左右反射，素材aa又在兩個中聲部、高中聲部交叉平移。

5.前后平移+上下反射。如對位曲4低聲部第120-122小節與中聲部第124-126形成上下反射，而中低聲部內各小節為前后平移。

6.前后平移+左右反射

如對位曲7第31-33小節。

第43-46小節音型是全曲的主題，反復出現，也經常以旋轉和反射的方式變形出現：第48-51小節為旋轉，第82-84小節為左右反射，而兩者之間是上下反射，形成反射和旋轉的組合。

（四）平移+旋轉，A+C，C+A，如對位曲10第29-30、第61-62小節

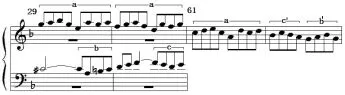
素材a在高中聲部前后、上下平移，素材b、c和b'c'在中低聲部旋轉。

（五）反射+反射，B+B，如對位曲2第38-40小節

素材aa'為上下反射，素材bb'為左右反射。

上述舉例，已將巴赫樂曲中的對稱，乃至所有音樂中的所有對稱的可能性全部囊括。這種以簡單的群即可囊括所有對稱形式，是數學語言“以簡馭繁、了無剩義”的最好體現。同時，所有對稱形式都可在巴赫的《賦格的藝術》中找到對應，也可見對稱在巴赫音樂創作中的重要性。

難道他對對稱及其組合表現形式有自覺的認識且以理性和科學的態度發掘完善它們？我們相信如此。

三、萬物至理

無論是音型，還是樂句，甚至完整的樂曲，對稱都是巴赫創作中的一個基本形式，而且是如貝爾所說“有意味的形式”。如何理解對稱形式中的意味？又如何理解巴赫乃至整個巴洛克時期音樂特別重視對稱？也許巴赫的“萬物至理”思想能讓我們窺探一二。

我們知道，自希臘以來，西方科學和藝術一直一脈相承著“萬物至理”的觀念，而藝術之用，常常就是要模仿和表現這種“至理”。在巴赫時代，宗教仍然深入人心，但科學已然不可遏制；信仰根深蒂固，但理性啟蒙勃興，那個時代的集大成者無不具有宗教和科學、信仰和理性的雙重面貌：雖然還無法擺脫如巴赫每每在手稿最后所寫“S.D.G”（Soli Deo Gloria 榮耀只歸于上帝），但隨著對數學、物理、天文學地深入探究和科學方法地傳播，人們越來越相信大至宇宙運行，小至鉛球落地，運動的規律所表現出的和諧，是一種客觀的理性和數學的優美，即如牛頓所言的“自然哲學的數學原理”。于是，“上帝創世之時就攜帶了數學——對事物的數進行考察的最簡單最神圣的抽象模型?！保?］14宇宙由上帝創造變成由上帝根據數學來設計，就使得“企圖理解上帝的意志及其創造物是最重要的”這一宗教教義，變成了探求上帝對自然的數學設計的科學活動。而對稱性就是這種設計原理的最深刻體現。比巴赫早半個世紀逝世的天文學家開普勒這樣描述宇宙和諧與音樂的關系：

所有天體的運動只不過是某種永遠傳唱的復調音樂。……換言之，人類或能利用多聲部音樂的美妙和聲，在瞬間就能表達出開天辟地以來的永恒，同時也由這種模擬上帝的音樂所散發的美感，體會到造物主對自己作品的滿足。［5］1048

這段話既是哥白尼所言“宇宙具有令人驚異的對稱性以及地球的運動和大小的已經確定的和諧聯系”［6］25思想的體現，也是西方語境中，“音樂作為最早的與上帝進行交流的語言”觀念的深化。從開普勒的音樂理想看，復調是對“天體和諧”的吟誦和模仿，如同莎士比亞在《威尼斯商人》第五幕中所云：“你所看見的每一顆微小的天體，在轉動的時候都會發出天使般的歌聲”［7］93——這讓我們想起賦格（fugue）的本意即“遁走”，乃是描述天體“無言而行，其聲如雷”。——音樂是與“上帝”交流的語音，且是唯一能夠循環往復無始無終的語言。所以巴赫所言音樂中的“萬物至理”，乃是以音樂去模擬上帝和天體之和諧。這是其時代宗教，亦是其時代科學觀念地體現。因此，羅杰·凱密恩特別提醒說：“在認識巴洛克風格時，對17、18世紀的科學發現有所了解也同樣有所幫助。”當我們被巴赫音樂中“規整的秩序、嚴密的邏輯架構所震撼”時，那是他在“用一個個音符，建構了深埋于表面音響的極其精密的客觀性的雄偉塔柱。”［8］別忘了，巴赫在他逝世前三年加入了“音樂科學通訊社”［9］。科學是巴赫晚年的一個探索主題，而《賦格的藝術》正是應通訊社之要求而提交的年度作品。

四、對稱的理想

巴赫《賦格的藝術》包含著他的音樂理想。其實，音樂本身就是一種理想。作曲家聽從自然、傳統和自我的召喚，用音符和結構摹寫它們，這種摹寫可能簡潔而樸素，因為樸素離自然和心靈的本真最近。藝術家越深入到自然和傳統中去，越細膩地感受心靈，他的思路就越開闊，創作也越簡潔，他就越懂得：萬物皆有至理，惟精惟一。因為二十世紀現代音樂中理性主義和數學思想的復活，我們再回頭看巴赫，會發現他比他之后的作曲家具有更多的現代性、對話性。歷史在想象中復活，在復活中解釋，在解釋中重生，希望我們對巴赫的研究就是如此?；堇赵f，當我們了解宇宙有多奇妙時，才開始體會其單純。同樣，我們說，當我們了解巴赫有多奇妙時，才開始體會其單純。物理學家威爾遜曾這樣描述科學與藝術的相通之處：“科學在描述大自然時以美學判斷為基本考量。物理學與藝術非常接近，都可由一粒沙看到大千世界；你看到了大自然的對稱性，以及各式各樣賞心悅目的形狀。終于，人們在欣賞雕塑或藝術作品時，也會開始領略到那些偉大的單純事物?！雹?/p>

［1］馬里奧·利維奧［美］，王志標譯.無法解出的方程——天才與對稱［M］.長沙.湖南科學技術出版社，2008.

［2］赫爾曼·外爾［德］，馮承天，陸繼宗譯.對稱［M］.上海：上?？平坛霭嫔?，2005.

［3］顧沛.對稱與群［M］.北京：高等教育出版社.2011.

［4］Johannes Kepler.Gesammelse Werke，ed.W.von Dyck，M.Caspar et al.，Munich，1938.

［5］Johannes Kepler.The Harmonies of the World.Book V［M］. translated by Charles Glenn Wallis. Great Books.vol.16.2006.

［6］哥白尼.天體運行論［M］.武漢.武漢出版社，1992.

［7］莎士比亞，朱生豪譯.莎士比亞戲劇集［M］.深圳.海天出版社，1999.

［8］何超.巴赫型音樂對波普爾“客觀知識”學說的影響［J］.山東科技大學學報（社會科學版），2012（04）.

［9］路多爾夫·維勒［德］，徐金梅譯.音樂中的平衡對稱［J］.音樂探索：四川音樂學院學報，1985（03）.

許金昕（1972—），女，湖北武漢人，鋼琴教育碩士，江漢大學音樂學院副教授，研究方向：鋼琴教學、鋼琴藝術史。