質量比對圓柱體雙自由度渦激振動的影響

宋振華，段夢蘭，任暉邦，邱　盼

(中國石油大學(北京) 海洋油氣研究中心，北京 102249)

?

質量比對圓柱體雙自由度渦激振動的影響

宋振華，段夢蘭，任暉邦，邱盼

(中國石油大學(北京) 海洋油氣研究中心，北京 102249)

通過數值模擬方法分析對比了質量比為2及質量比為10的立管在約化速度3～14的雙自由度渦激振動特性。質量比為2的圓柱具有更寬的鎖定區間，且相同約化速度下橫向振幅更大。從振動軌跡可以看出，質量比為2的立管在鎖定區間內順流向振動振幅不可忽略，在鎖定區間外順流向振動極小。質量比為10的立管在鎖定區間內順流向振動極小，鎖定區間外順流向振動振幅不可忽略。

圓柱體；流固耦合；渦激振動；質量比

海洋工程上普遍采用圓柱形斷面的結構物，因此當海流經過這些圓柱形的結構物后，其后方會產生卡門渦街。當這些圓柱形結構物為彈性支撐或是細長的柔性結構時，由于卡門渦街的作用會引發渦激振動。例如海洋工程上常用的浮標、海洋立管、導管架平臺樁腿等都是典型的圓柱形海洋結構物。

對于這類典型的流固耦合問題，早期研究主要以水池或風洞實驗為主，1968年Feng在風洞中研究了質量比為248的圓柱體的橫向渦激振動響應，發現振幅為0.8D(D為圓柱體直徑)[1]。2009年F.J.Huera-Huarte通過水槽試驗，研究了長1.5 m，直徑16 mm，質量比為1.8的細長圓柱體的渦激振動，其橫向振幅為0.7D，順流向振幅為0.2D[2]。隨著流體力學理論和計算流體動力學的不斷發展，近年來很多學者開始采用數值模擬的方法來研究渦激振動的問題。例如Zhao Ming在2005年針對雙管進行了固定圓柱繞流的單向流固耦合數值模擬研究[3]。2009年徐楓等針對不同截面形狀柱體進行了CFD數值模擬渦激振動，并發現圓柱和六邊形柱表現為渦激振動，而方柱和三角形柱則發生低頻馳振向高頻渦激振動轉化的現象[4]。2011年盛磊祥，陳國明對并列管的渦激振動參數進行了分析[5]。2012年范杰利等針對兩自由度渦激振動通過數值模擬方法研究長徑比對渦激振動振幅及鎖定區間的影響[6]。本文針對圓柱形結構物的渦激振動進行流固耦合數值研究，在質量比為2及質量比為10兩種條件下，對比分析橫向振動的振幅與順流向振動的振幅的變化及鎖定區間的變化，以及在不同約化速度下圓柱體的運動軌跡。

1　數值模型

對于柱體振動模型可簡化為質量-彈簧-阻尼系統，雙自由度為兩個平動自由度，方向分別為順流向和橫流向，如圖1所示。計算域采用40D×20D的矩形流場，考慮入口端對圓柱的影響，流場入口距圓柱中心為10D；考慮尾流中的渦街不被出口邊界影響，因此出口邊界距離圓柱中心距離為30D；橫向邊界距離圓柱中心為10D，采用slip wall邊界條件，D為與來流方向垂直的特征長度，本文中為圓柱直徑。流場示意圖如圖2所示。

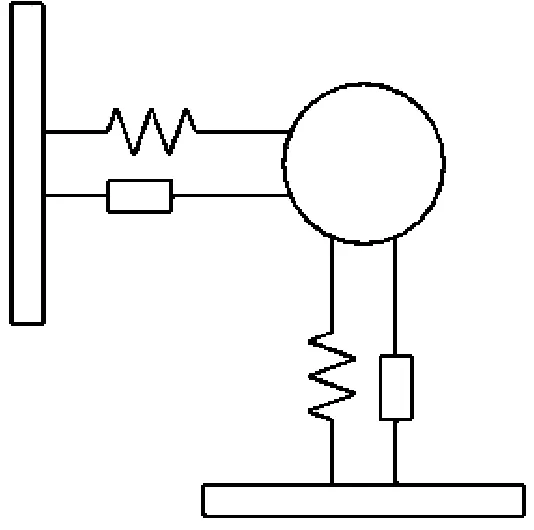
圖1　圓柱體彈性支撐振動模型

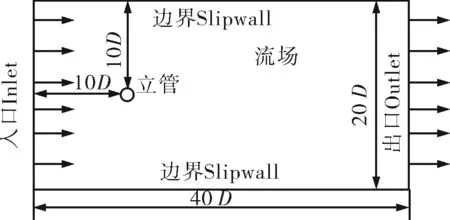
圖2　流場模型示意

直角坐標系下，流體域的連續性方程和動量方程分別表達如下：

·u=0

(1)

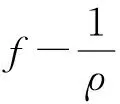
(2)

圓柱振動方程為：

(3)

(4)

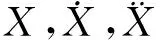
(5)

Mr=ms/ml

(6)

式中：Uγ為約化速度；Mr為結構物與流體的質量比；ms結構物的質量；ml為結構物排開流體的質量。

本文中，針對Mr=2和Mr=10進行研究。

2　網格劃分

對整個流體域進行網格劃分，網格的質量對計算精度和計算速度有很大影響，高精度會使結果更加準確，但當網格精度達到一定數量后，對精度的影響十分有限。此時，過大的網格數量只會增加計算量，延長計算時間。因此，對網格數量需要有合理的控制。本文中流體域網格總數為18萬左右，如圖3所示。對重要部分進行加密處理，以保證計算的準確性。對于圓柱橫流向和順流向的方向，網格密度較高。因為圓柱前方是流體力作用的高壓區，后方是渦街釋放區，兩側是泄渦的分離點。對圓柱周圍建立邊界層，如圖4所示，以保證計算的精度。

圖3　流場域網格劃分

圖4　流場域中圓柱體邊界層網格

3　結果分析

渦激振動具有強烈的雙向流固耦合特征，對于彈性支撐的柱體，流體與柱體之間的相互作用主要取決于流體及固體相關屬性，即流體的密度和流速，柱體的質量及剛度。本研究中流體為水，密度為1 000 kg/m3，流速為0.015 m/s。柱體為圓柱，質量比Mr=2及Mr=10。約化速度Ur=3～14的圓柱體渦激振動的振幅和頻率。

3.1橫流向振幅

圓柱體渦激振動的主要振動為橫流向振動，因為橫流向振動振幅通常遠大于順流向振幅，橫向振動的鎖定區間通常位于Ur=5～8范圍內。

如圖5所示，當Mr=2時，橫流向振動的鎖定區間在Ur=4～7內，Ur=3時，振幅Ay/D=0.12；Ur=8時，振幅Ay/D=0.11，為鎖定區間的邊界點。Ur=4時，振幅Ay/D=0.55；Ur=5時，振幅Ay/D=0.56達到振幅最大值。雖然Ur=4時，振幅最大值為0.55，但此時振幅在0.33～0.55周期性變化。

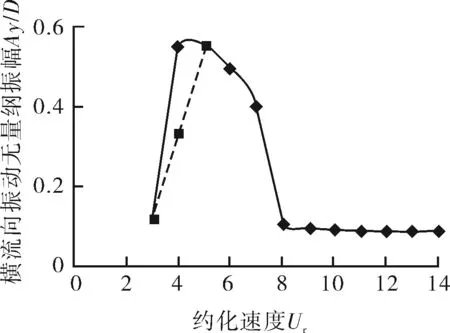
圖5　質量比Mr=2時橫流向鎖定區間

如圖6所示，當Mr=10時，鎖定區間為Ur=4～8，當Ur≥12時，Mr=10的橫流向振幅小于Mr=2時的橫流向振幅。Mr=4時，橫向振幅很小，不在鎖定區間內，并且不存在周期性變化的振幅。Ur=5時，橫向振幅達到最大值Ay/D=0.48，小于Mr=2，Mr=5時的橫向振幅最大值。

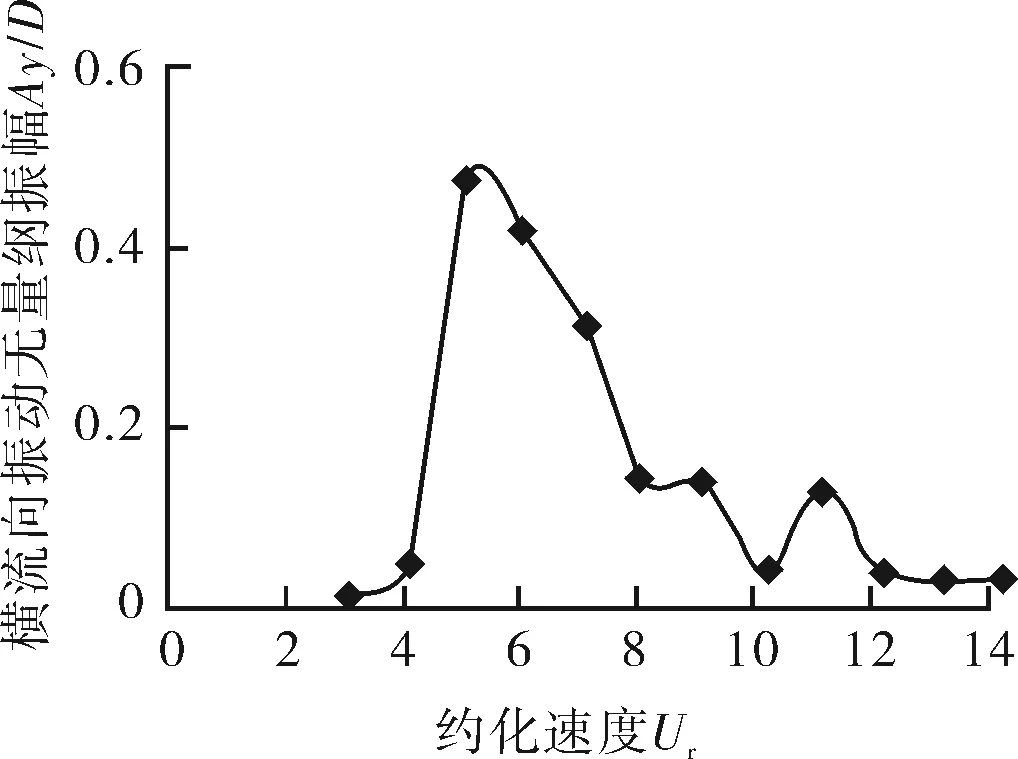
圖6　質量比Mr=10時橫流向鎖定區間

由以上分析可以看出，質量比較大時，橫流向的鎖定區間變窄，振幅減小。

3.2順流向振幅

圓柱體渦激振動中順流向振動相對于橫流向振動的振幅較小，但頻率較高。通過研究發現，當Mr=2時，順流向振動同樣存在鎖定區間，Ur=4～7，并且Ur=4時，順流向振動的振幅在0.075～0.024之間周期性變化，如圖7所示。當Mr=10時，順流向振幅沒有鎖定區間，可以看到Ur=3～8時，順流向振幅較小，而當Ur>9時，順流向振幅開始增加，并且隨著Ur的增大，不斷增大，如圖8所示。

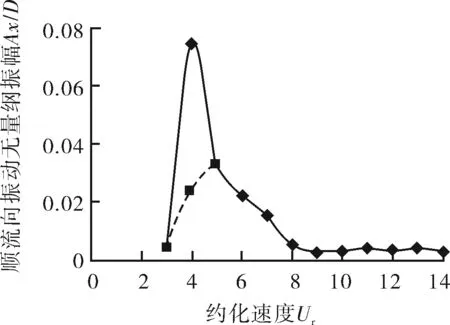
圖7　質量比Mr=2時順流向鎖定區間

圖8　質量比Mr=10時順流向鎖定區間

3.3不同約化速度下的振動軌跡

如圖9所示，Mr=2，在Ur=3～14，振動皆為“8”字型軌跡。橫流向振動的振幅始終大于順流向振動的振幅。隨著剛度的減小，順流向振動的平均位置逐漸增大，最大位置處于Ur=4～7的鎖定區間內。當Ur=4時，振動軌跡在較小“8”字型到大“8”字型不斷循環。在Ur=3～7，可以看到“8”字型特征明顯，說明順流向振幅幅值較大，此時順流向振動不可忽略。當Ur≥8時，順流向振幅減小，此時振動軌跡近似于直線。

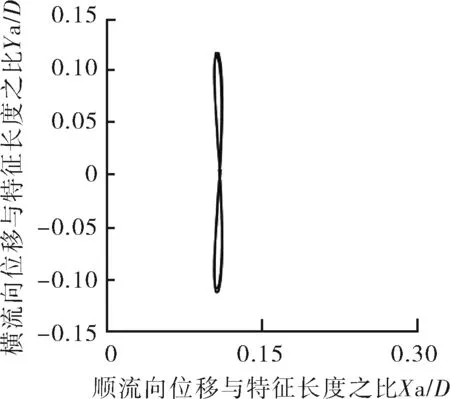
a　約化速度Ur=3

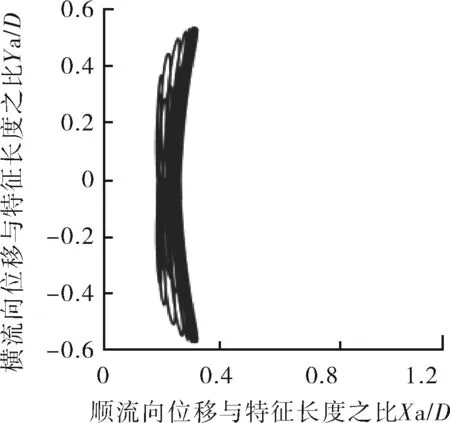
b　約化速度Ur=4

c　約化速度Ur=5

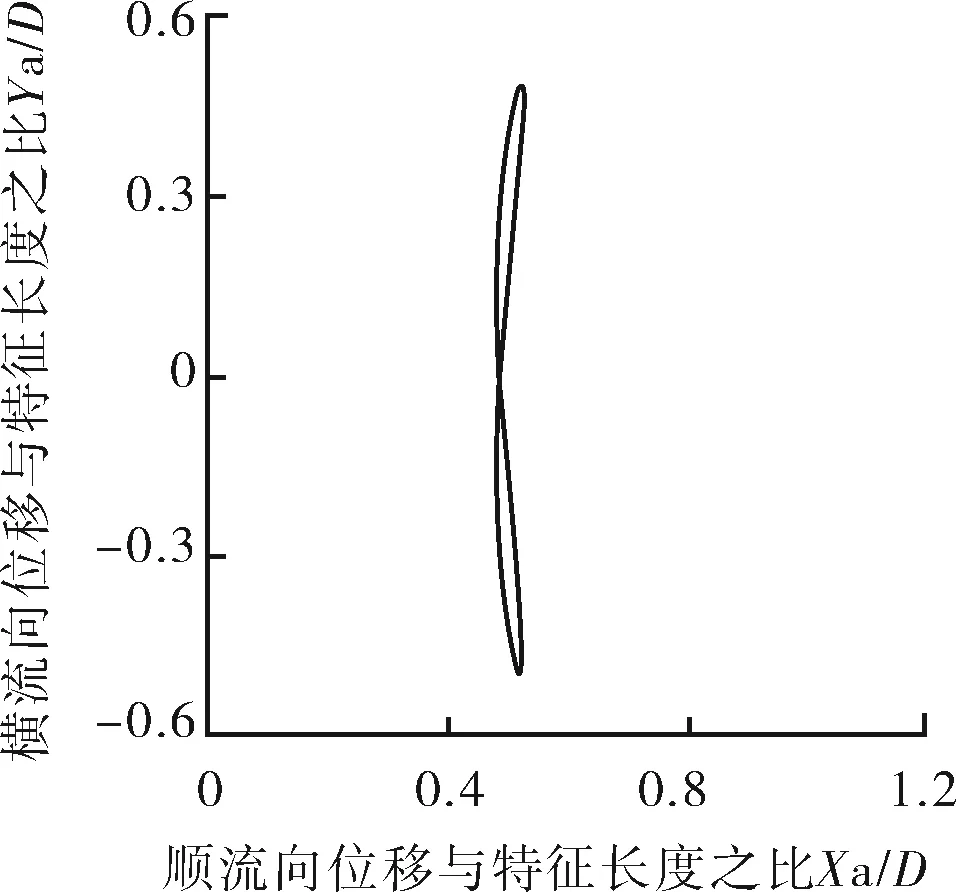
d　約化速度Ur=6

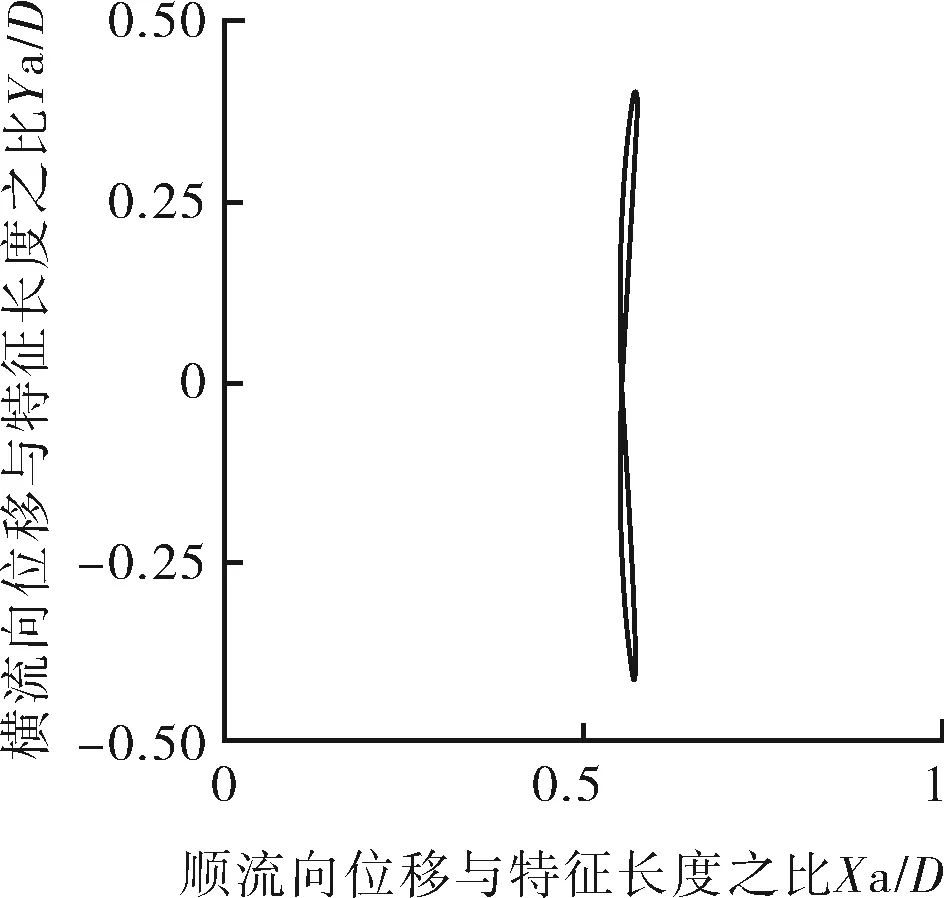
e　約化速度Ur=7

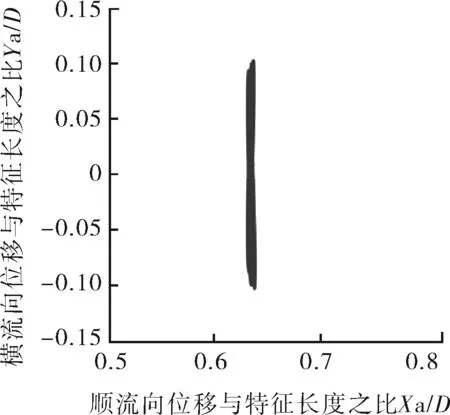
f　約化速度Ur=8

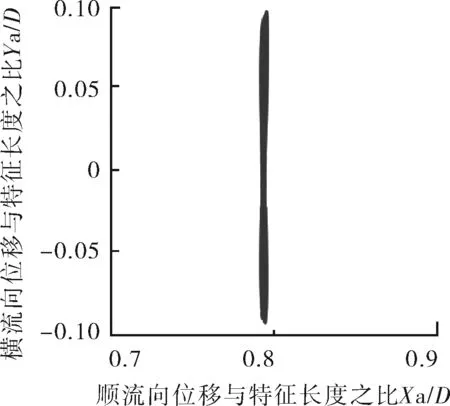
g　約化速度Ur=9

h　約化速度Ur=10

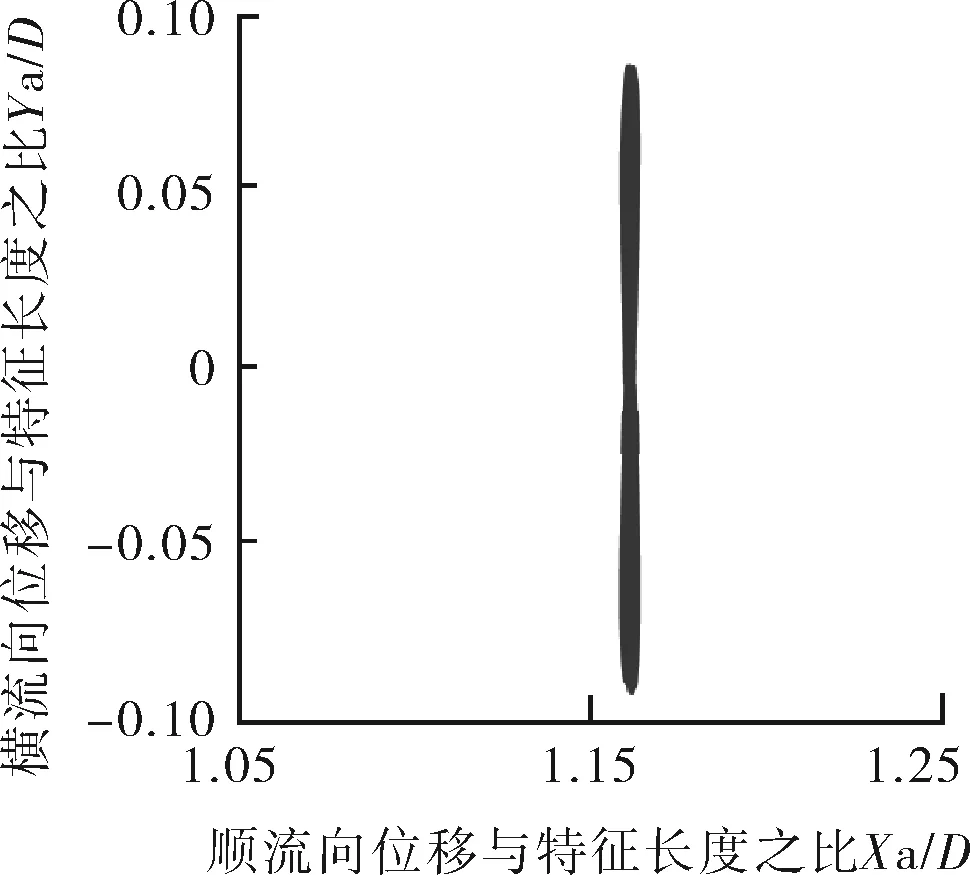
i　約化速度Ur=11

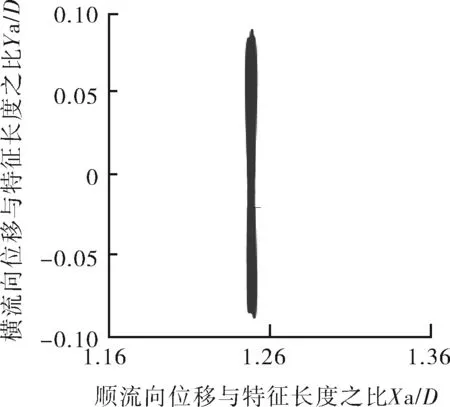
j　約化速度Ur=12

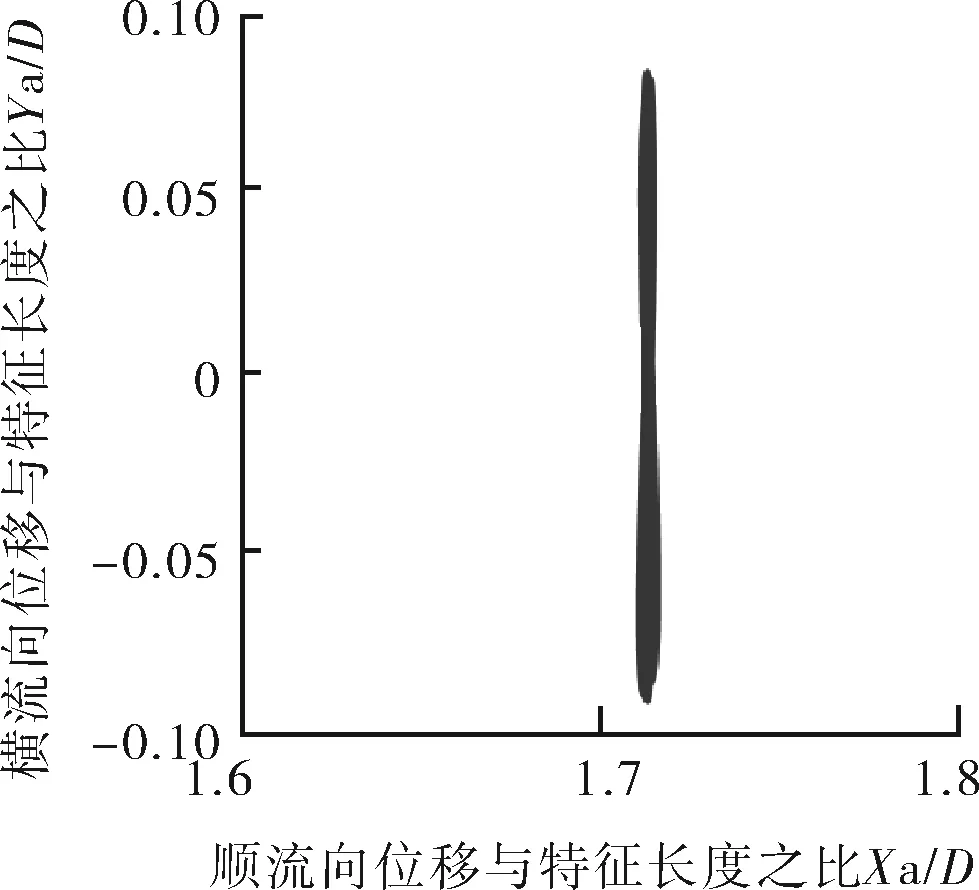
l　約化速度Ur=14

如圖10所示，Mr=10，在鎖定區間Ur=4～7，順流向振動的平均位置變化不大，都在0.1D范圍內，當Ur≥8時，順流向振動的平均位置明顯增大。說明此時約化速度對順流向振動的平均位置影響較大。Ur=4～7，振動軌跡雖有“8”字型特點，但是可以看到橫流向振動幅值極小，此時振動軌跡近似于橫流向的直線振動。Ur=8，9時，順流向振動可見。當Ur=3，10～14時，順流向振動振幅與橫流向相當。特別是當Ur=10，12，13，14時，可以清楚地看到，此時橫流向振幅小于順流向振幅，并且呈現出“∞”字型軌跡。

因此，對于Mr=2，Ur=3～7，順流向振動不可忽略。Mr=10，Ur=3，8～14，順流向振動不可忽略。Ur=4～7，Mr=2，Mr=10的振動軌跡都表現為“8”字型振動軌跡。

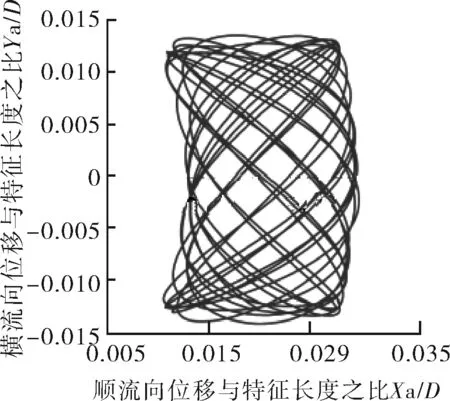
a　約化速度Ur=3

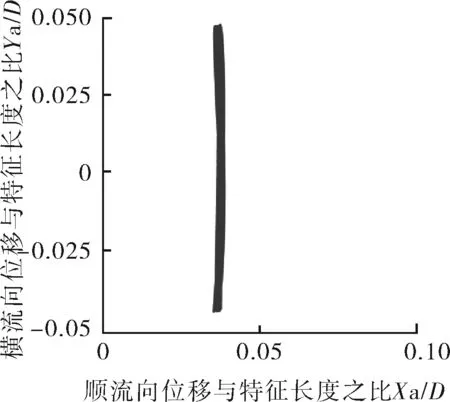
b　約化速度Ur=4

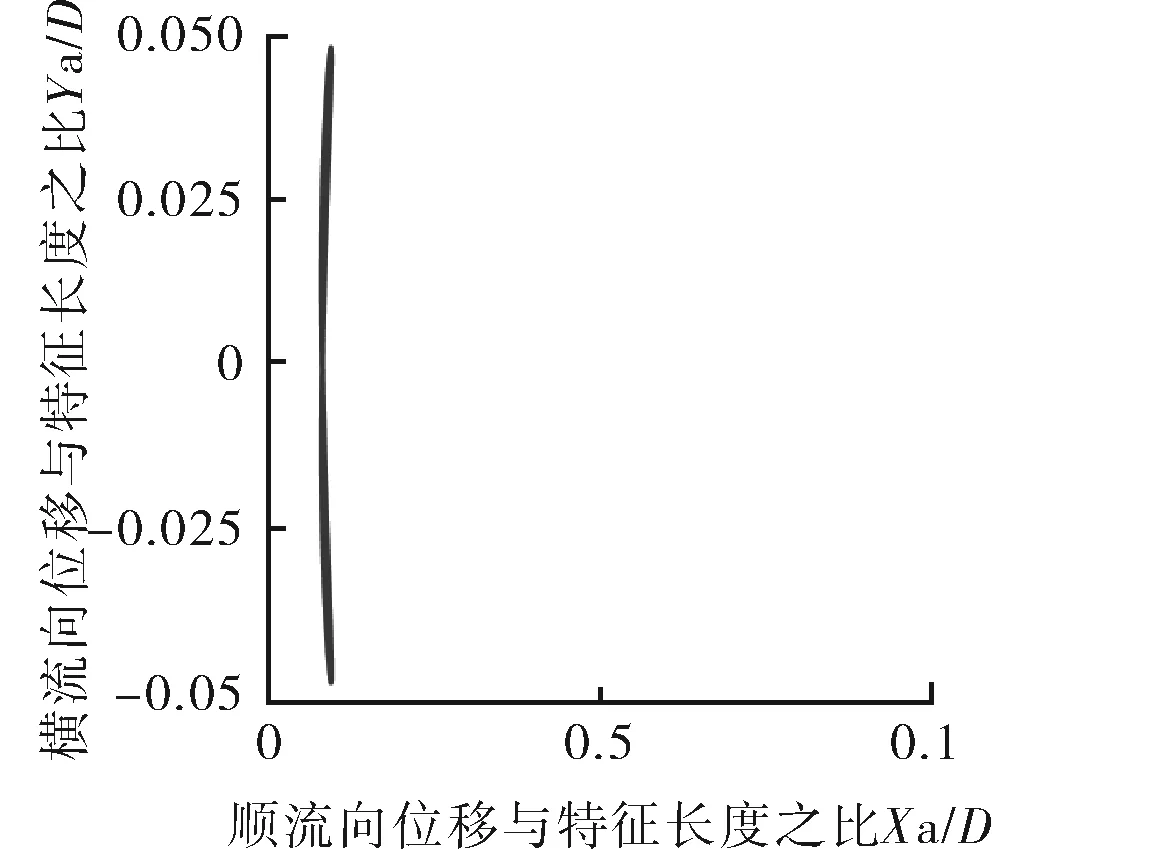
c　約化速度Ur=5

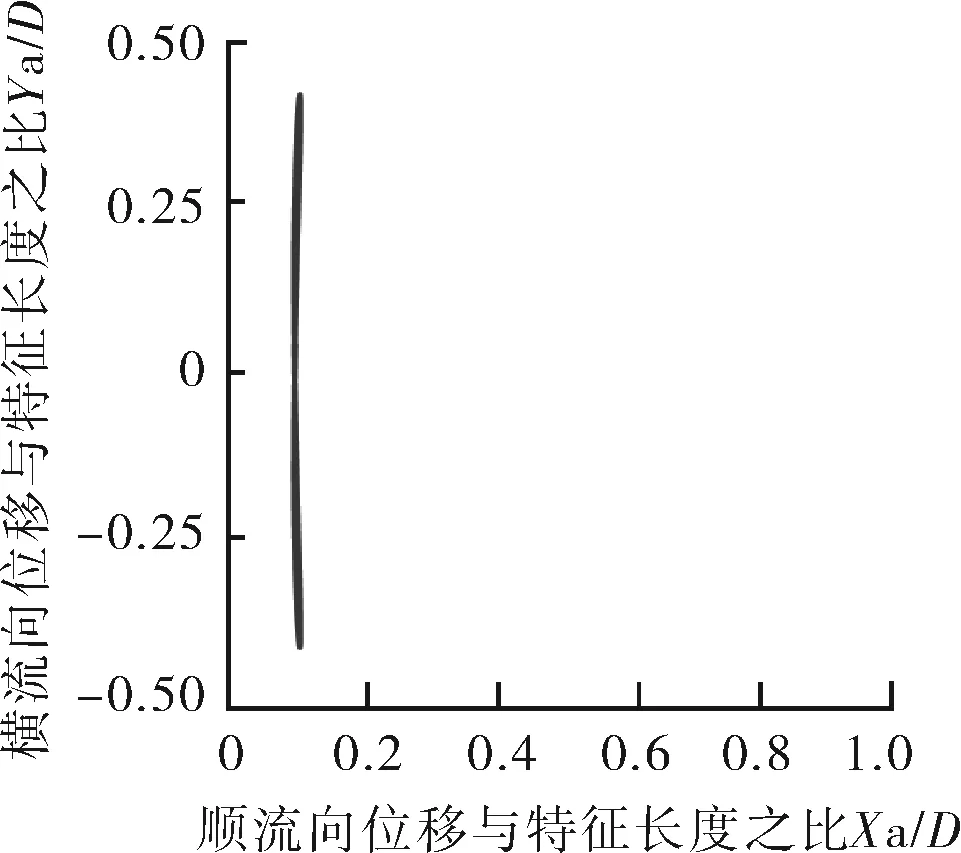
d　約化速度Ur=6

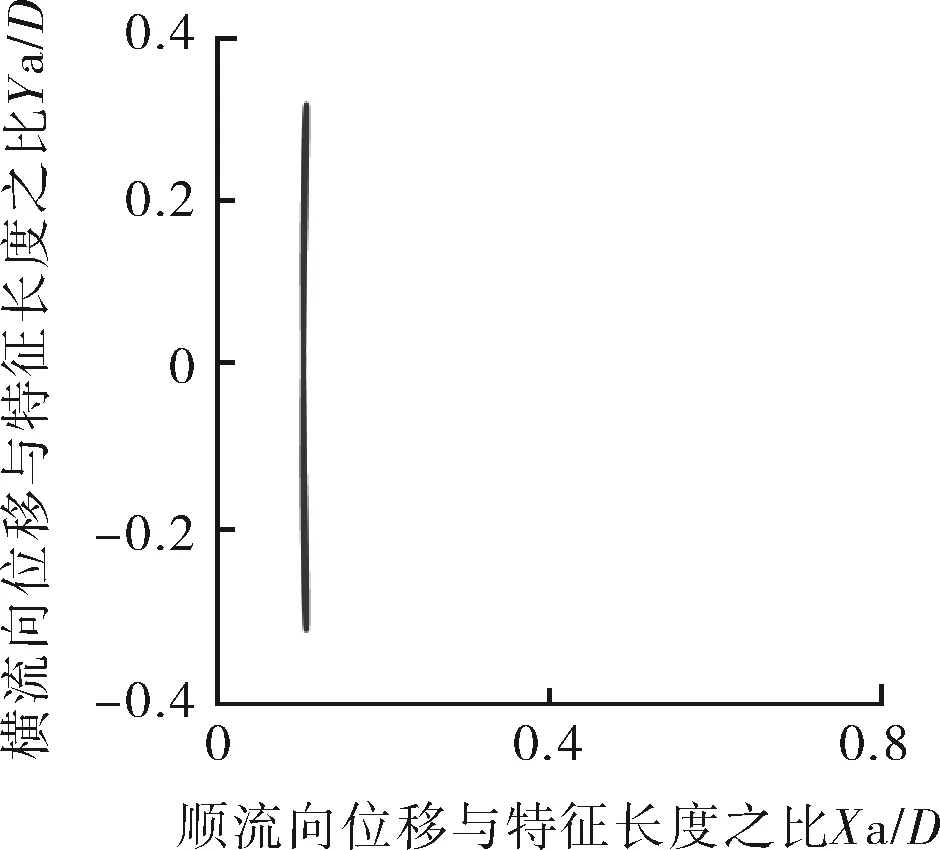
e　約化速度Ur=7

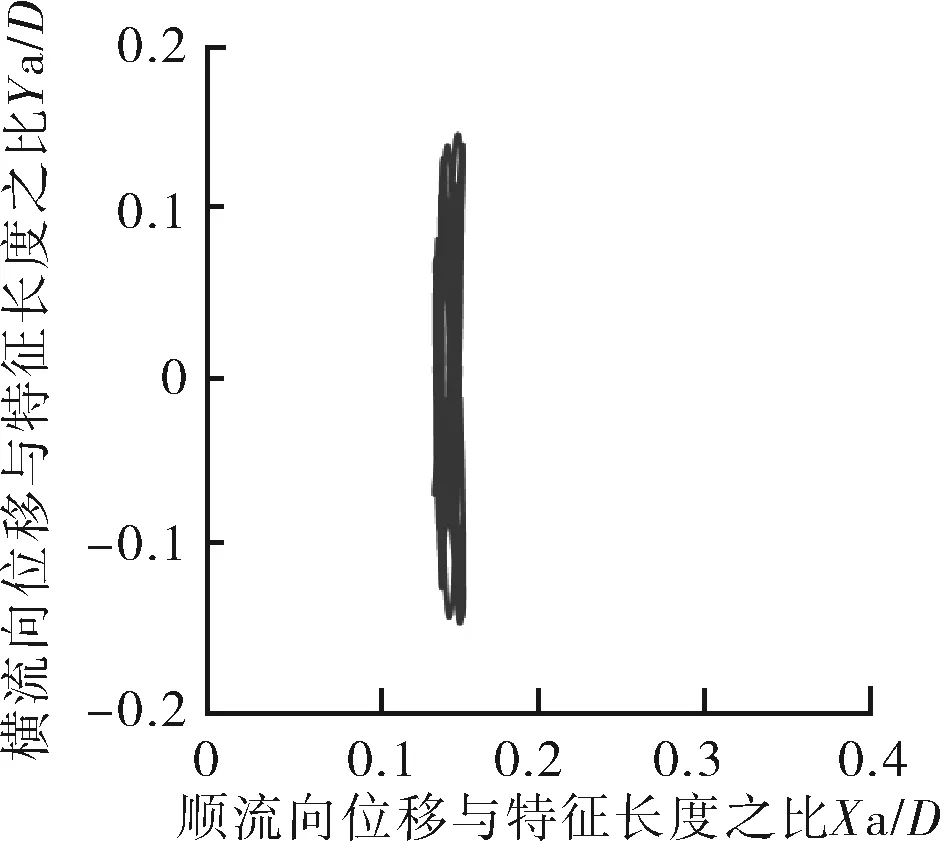
f　約化速度Ur=8

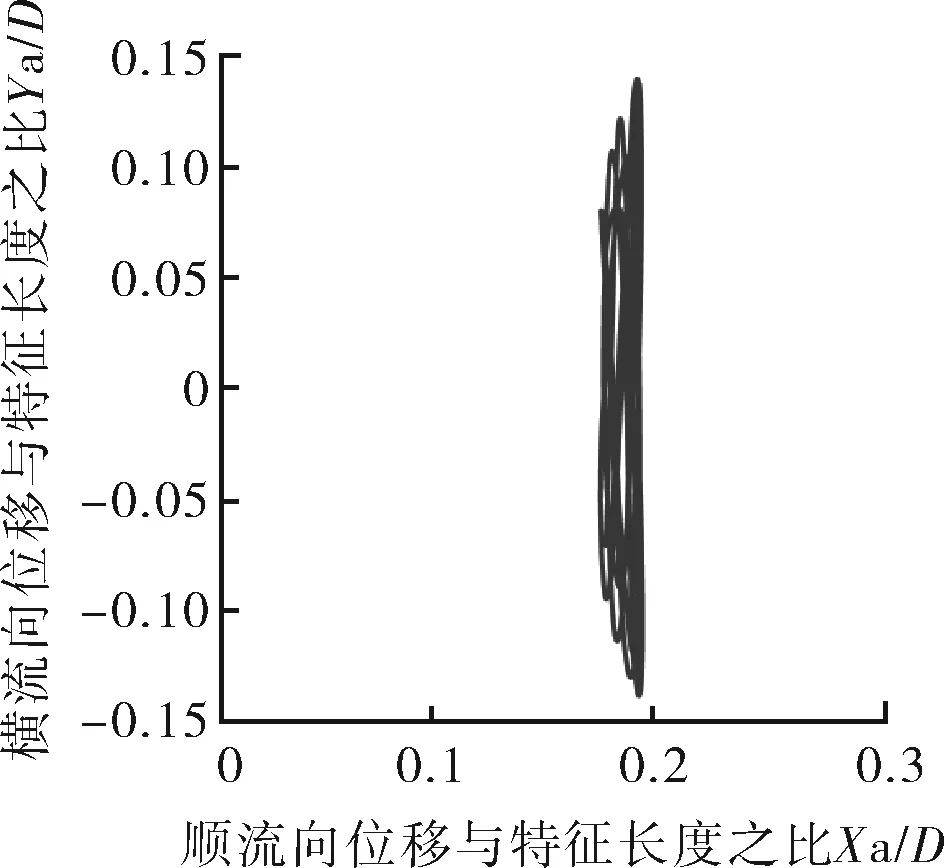
g　約化速度Ur=9

h　約化速度Ur=10

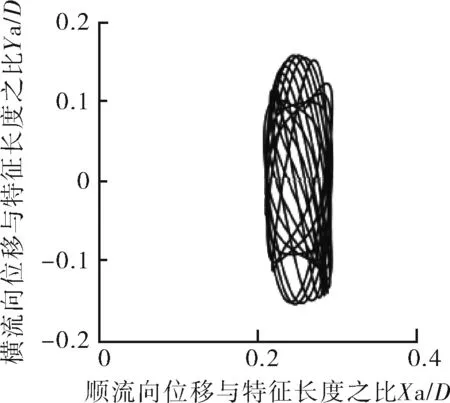
i　約化速度Ur=11

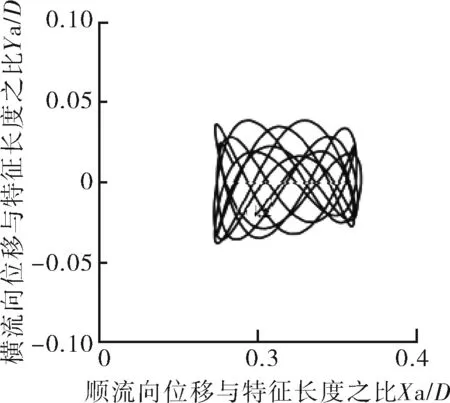
j　約化速度Ur=12

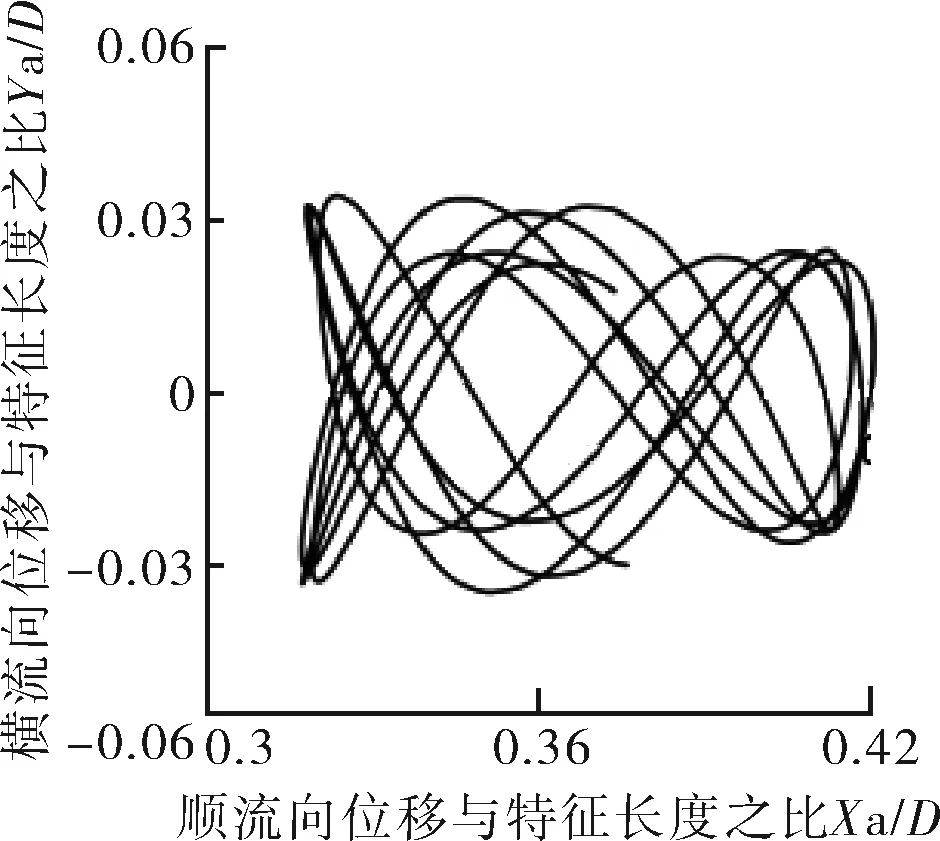
k　約化速度Ur=13

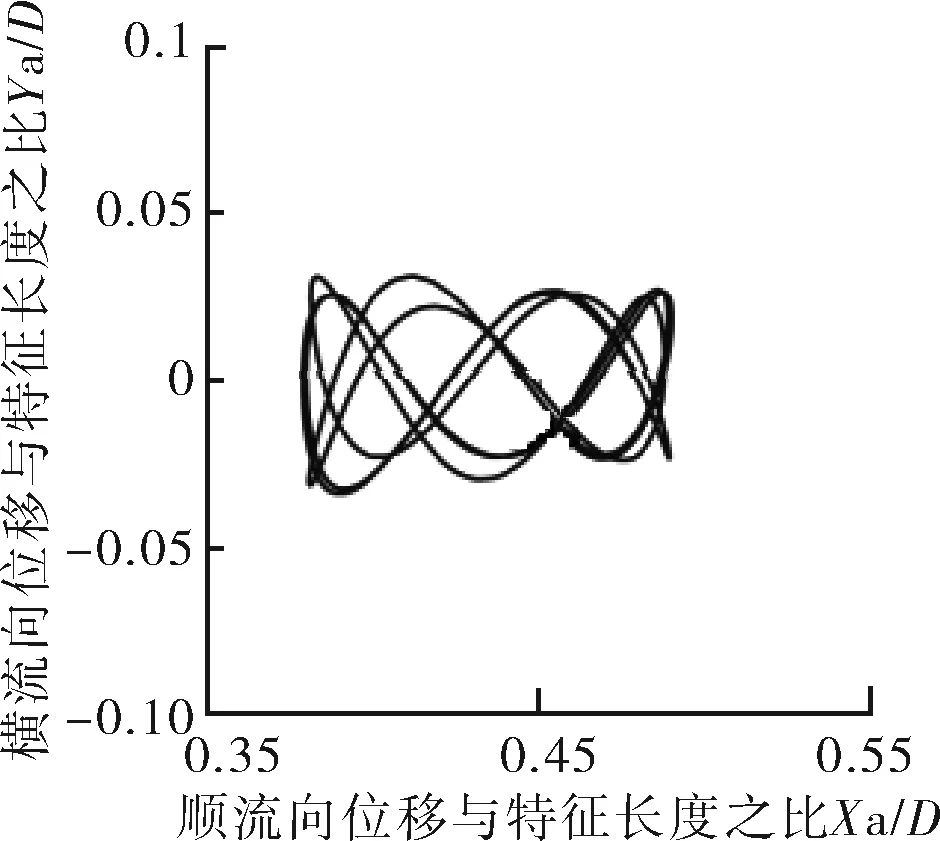
l　約化速度Ur=14

4　結論

1)本文對質量比為2和質量比為10的雙自由度雙向流固耦合渦激振動進行了研究。

2)橫流向振動。相同約化速度下，質量比為2時的橫流向振幅大于質量比為10時的橫流向振幅。質量比為2的橫流向振動比質量比為10的橫流向振動具有更寬的鎖定區間。

3)順流向振動。質量比為2時順流向振動存在與橫流向振動類似的鎖定區間，鎖定區間為約化速度Ur=4～7；質量比為10時順流向振動在約化速度3～9區間內振幅較小，當約化速度大于10后，開始迅速增加。隨著約化速度的增大，兩種質量比下的圓柱體順流向振動的平均位置均有所增大。

4)振動軌跡。質量比為2時，在鎖定區間內，順流向振動明顯，振動軌跡呈現出明顯的“8”字型，當約化速度大于8時，由于順流向振幅減小，振動軌跡接近于橫流向的直線振動。質量比為10時，鎖定區間內，順流向振動很小，振動軌跡接近于橫流向的直線振動；鎖定區間外，順流向振動明顯，特別是當約化速度為3，10～14時，順流向與橫流向振動振幅相當，當約化速度為12～14時，振動軌跡表現為“∞”字型。

[1]Feng C C.The Measurements of Vortex-Induced Effects in Flow Past a Stationary and Oscillating Circular and D-Section Cylinders[D].University of British Columbia，1968.[2]Huera-Huarte F J，Bearman P W.Wake structures and vortex-induced vibrations of a long flexible cylinder[J].Journal of Fluid and Structures，2009(25)：969-990.

[3]Zhao Ming，Cheng Liang，Teng Bin.Numerical simulation of viscous flow past two circular cylinders of different diameters[J].Applied Ocean Research，2005(27)：39-55.

[4]徐楓，歐進萍，肖儀清.不同截面形狀柱體流致振動的CFD數值模擬[J].工程力學，2009，6(4)：7-15.

[5]盛磊祥，陳國明.海洋并列立管渦激振動參數分析[J].石油礦場機械，2011，40(3)：5-8.

[6]范杰利，黃維平.細長立管兩自由度渦激振動數值研究[J].振動與沖擊，2012，31(24)：65-68.

Influence of Mass Ratio on Two-freedom VIV of a Circular Cylinder

SONG Zhenhua，DUAN Menglan，REN Huibang，QIU Pan

(Offshore Oil & Gas Research Center，China University of Petroleum (Beijing)，Beijing 102249，China)

Two-freedom VIV by numerical simulation are investigated in this paper.The computation is carried out for reduced velocities in the range 3≤Ur≤14 and mass ratios=2，10.The lock-in region of mass ratio 2 is wider than that of mass ratio 10.The amplitudes of cross flow of mass ratio 2 are larger than that of mass ratio 10 at the same reduced velocities.The in-line flow vibration can’t be neglected in lock-in region for mass ratio 2.On the contrary，the in-line flow amplitude reaches the same magnitude of cross flow amplitude out of the lock-in region.

cylinder；fluid solid interaction；VIV；mass ratio

1001-3482(2016)05-0013-07

2015-11-26

國家重點基礎研究發展計劃(973計劃)“深海柔性結構的非線性流固耦合與破壞機理研究”(2011CB013702)

宋振華(1983-)，男，黑龍江大慶人，博士研究生，主要研究方向：流固耦合數值模擬，動力學分析計算，E-mail：thzh83@163.com。

TE95

A

10.3969/j.issn.1001-3482.2016.05.003