帶乘性噪聲附等式約束的非線性系統濾波算法*

王昌盛，張　玲，臧愛云，王　琨

(中國海洋大學工程學院，山東省高校海洋機電裝備與儀器重點實驗室 山東 青島 266100)

?

帶乘性噪聲附等式約束的非線性系統濾波算法*

王昌盛，張玲，臧愛云，王琨

(中國海洋大學工程學院，山東省高校海洋機電裝備與儀器重點實驗室 山東 青島 266100)

隨著控制理論與計算機的飛速發展，非線性濾波已在各領域得到廣泛應用。本文針對一類帶乘性噪聲附等式約束非線性系統，提出了一種狀態濾波算法。該算法首先將狀態方程和觀測方程分別通過泰勒公式展開，得到新的帶乘性噪聲附等式約束的線性系統模型，然后通過最優觀測的方法將觀測方程擴維，再基于投影定理進行求解得到濾波算法，最后通過仿真驗證了算法的有效性。

乘性噪聲； 等式約束； 非線性濾波;投影定理； 最優觀測

引用格式：王昌盛， 張玲， 臧愛云. 帶乘性噪聲附等式約束的非線性系統濾波算法[J].中國海洋大學學報(自然科學版), 2016, 46(8): 137-140.

WANG Chang-Sheng，ZHANG Ling，Zang Ai-Yun. Filtering algorithm for nonlinear systems with equation state constraints and multiplicative noise[J].Periodical of Ocean University of China, 2016, 46(8): 137-140.

隨著控制理論與計算機技術的飛速發展，非線性濾波已在通信與信號處理、航空航天、導航定位等眾多領域得到了越來越廣泛的應用，觀測手段的豐富使得對于物理特征及現象有了更深入的了解，從而得到更多的先驗信息，建立約束，結合非線性濾波，可以提高濾波精度。

國內外的眾多學者針對帶有約束條件的非線性系統濾波做了大量的研究工作。Simon J等人系統地闡述了非線性等式約束的卡爾曼濾波算法[1]，KandePu等人和Brunoo等人研究了等式約束無跡卡爾曼濾波算法[2]，Simon D概述了狀態約束的卡爾曼濾波的線性和非線性算法[3]，X Fu等人利用卡爾曼濾波對于線性和非線性混合約束下的系統進行濾波[4],Linfeng Xu等人在對于約束不是嚴格要求的條件下，提出了卡爾曼濾波的線性和非線性算法[5],劉杰將等式約束轉化成凸二次規劃，給出了約束濾波估計值的顯式表達式[6]。

盡管對帶等式約束的非線性系統濾波的研究進行了深入研究，但其算法大都建立在一般狀態空間模型，而在實際系統中，往往還存在著乘性噪聲，而帶乘性噪聲系統在非線性系統[7]、水聲通信[8]、故障檢測[9]、衛星姿態估計[10]等領域有了廣泛的應用。

本文針對帶乘性噪聲附等式約束的非線性系統的濾波算法進行了研究。通過泰勒展開、狀態擴維等方法以及投影定理得到了帶乘性噪聲附等式約束非線性系統的濾波算法。

1　模型描述

1.1 非線性模型

對于帶乘性噪聲非線性系統，其狀態空間模型為：

xk=f(xk-1)+wk，

(1)

zk=mkh(xk)+vk。

(2)

其中：xk∈Rm為狀態向量；zk∈Rn為量測向量；wk∈Rr為系統噪聲；vk∈Rn為量測噪聲；mk為一維乘性噪聲，f()、h()分別是m、n維非線性向量函數。設系統滿足以下條件：

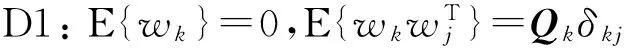
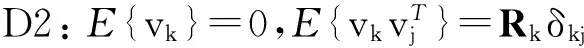
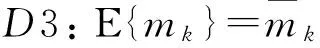
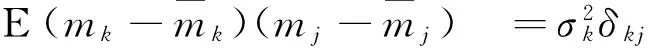
D5：隨機序列{mk},{wk},{vk}及初始狀態x0彼此相互統計獨立。

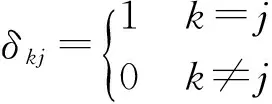
假定系統(1)(2)有如下狀態約束：

Dkxk=dk。

(3)

其中：Dk是s×m階常量矩陣；dk是s×1階常向量。s是狀態約束量。并且s≤m。本文假設Dk是滿秩矩陣，且秩為s階。

1.2線性模型

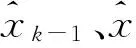
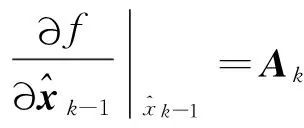
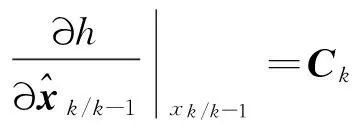
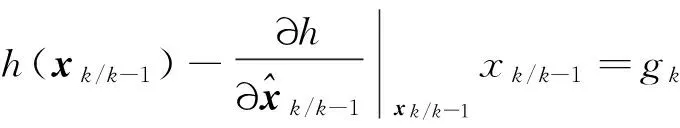
則原系統的近似狀態空間表達：

xk=Akxk-1+uk+wk，

(4)

zk=mkCkxk+mkgk+vk。

(5)

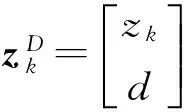
xk=Akxk-1+uk+wk，

(6)

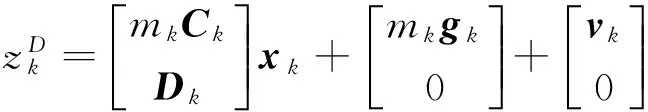
(7)

2　算法推導

針對(6)、(7)帶乘性噪聲附等式約束的系統，有如下定理：

定理對于式(6)、(7)的系統滿足假設條件，則有如下的狀態濾波遞推算法：

狀態濾波估計

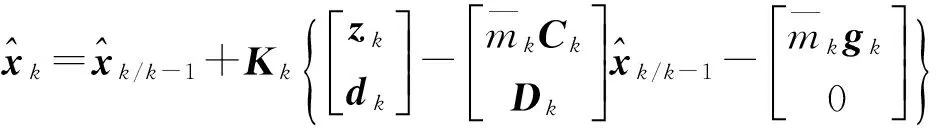
(8)

狀態一步預測

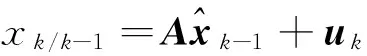
(9)

增益矩陣

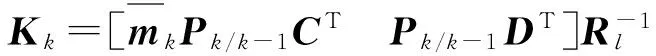
(10)

輸出殘差方差陣

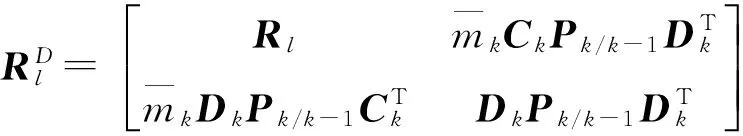
(11)

其中

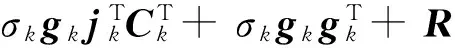
(12)

狀態相關矩陣

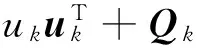
(13)

狀態均值

jk=E[xk]=Ajk-1+uk-1。

(14)

一步預測誤差方差陣

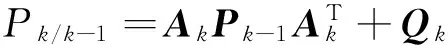
(15)

誤差方差陣

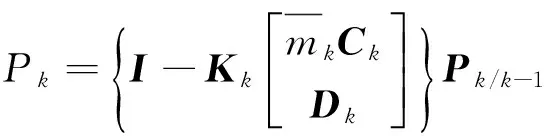
(16)

初值：

x0/0=E(x(0))。

(17)

P0=S(0)。

(18)

證明針對(4)、(5)，由投影定理得，

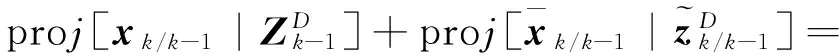
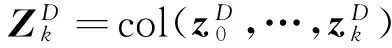
狀態一步預測為

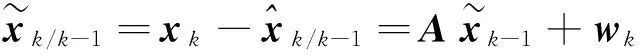
由假設條件及投影定理公式，有觀測一步預測為

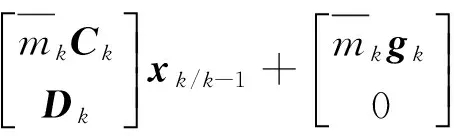
而輸出殘差為

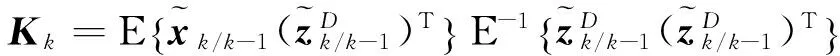
其中

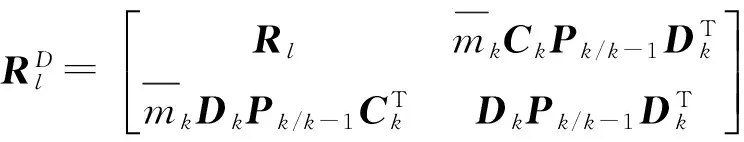
其中

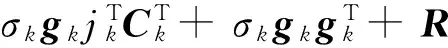
其中

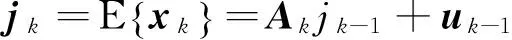
可得一步預測誤差方差陣

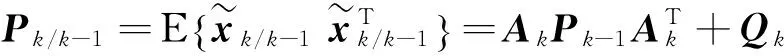
濾波誤差

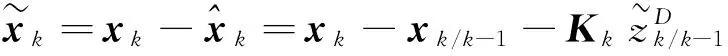
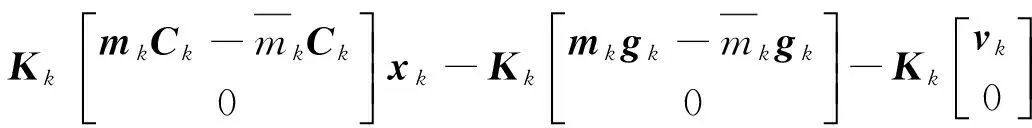
誤差方差陣

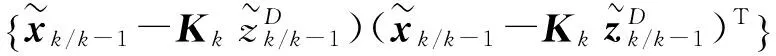
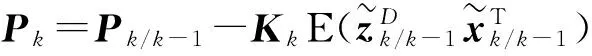
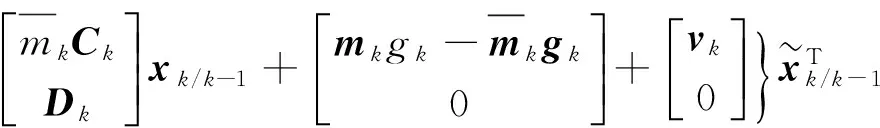
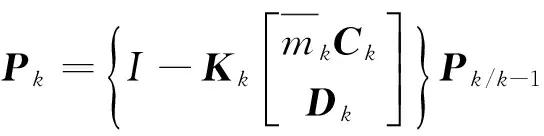
至此，算法推導完畢。

3　算法仿真

假設一輛行駛中的汽車，狀態x的前兩個狀態分量是地面車輛的北坐標和東坐標，后兩個狀態分量由北方向速度和東方向速度表示。給出系統的運動模型：

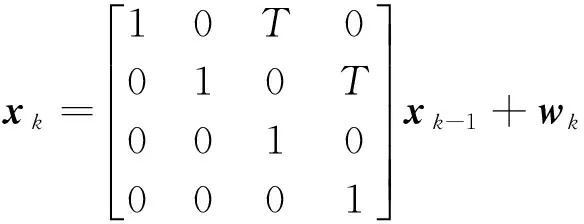
用一個參考點來確定其行駛路線，即(x0,y0)，取為(100,100)，其中每個參考點都是通過汽車的北方向與東方向位置來定的，在運動期間不可避免的存在抖動振動的影響，為了更客觀的描述測量模型的隨機干擾，還要考慮乘性噪聲，則系統的觀測模型為：

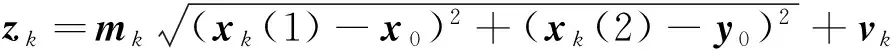
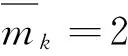
Dkxk=dk，其中

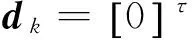
利用Matlab對本文的算法進行仿真，歷元總數為100s，北方向跟蹤效果如圖所示。

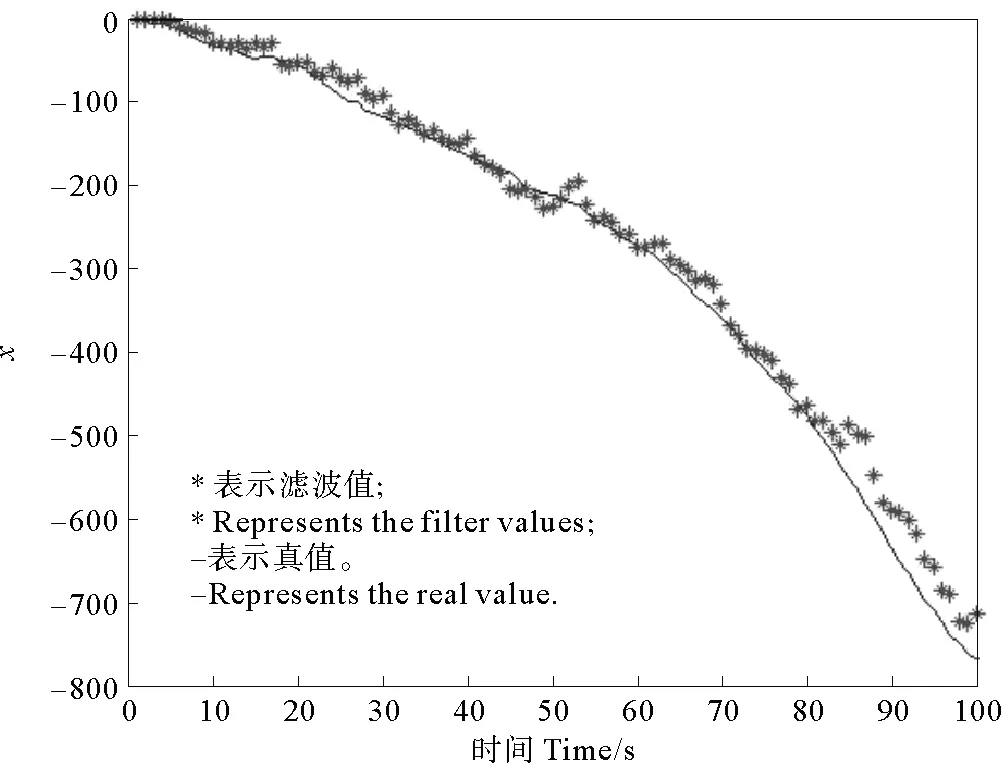
圖1　北方向的真值和濾波值

圖1給出了狀態第一分量,既北方向的濾波結果。圖中示出了狀態第一分量的真值和濾波值，從整體趨勢上來看，跟蹤效果明顯，驗證了算法的有效性。

圖2為狀態第一分量真值和濾波值的相對誤差值，濾波相對誤差平穩，但一直存在，但這是由于將系統模型線性化時，去掉了泰勒展開的高階項后，模型的不精確造成的，同時由于帶乘性噪聲系統結構的復雜性，這個問題涉及到線性模型轉化的方面，是以后要繼續研究的方向。

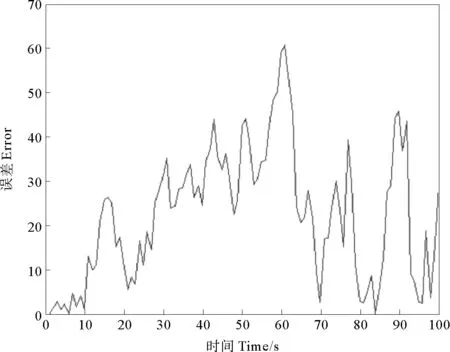
圖2　北方向的真值和濾波值相對誤差

4　結語

針對等乘性噪聲附等式約束的非線性系統的狀態濾波問題，該算法通過泰勒公式將系統的狀態方程和觀測方程展開，得到線性系統，利用觀測最優的方法對觀測方程進行擴維，最后利用投影定理對變形后的系統進行濾波求解。仿真結果驗證了本文算法的有效性。

本文的算法也存在著不足，只考慮了擴展卡爾曼濾波的方法，還沒有分析線性化對于誤差的影響，同時關于非線性系統的濾波方法還有其他方法沒有考慮。

[1]Julier S J， LaViola J J J L. On Kalman filtering with nonlinear equality constraints [J]. IEEE Transactions on Signal Processing, 2007,55(6): 2774-2784.

[2]Kandepu R, Imsland L, Foss B. Constrained state estimation using the unscented Kalman filter[C]. Ajaccio, France: 16th Mediterranean Conference on Control and Automation, 2008: 1453-1458

[3]Simon D. Kalman filtering with state constraints: A survey of linear and nonlinear algorithm[J]. IET Control Theory and Applications, 2010, 4(8): 1303-1318.

[4]Fu X, Jia Y, Du J, et al. Kalman Filtering with Multiple onlinear-linear Mixing State[C]. 49th IEEE Conference on Decision and Control ecember 15-17, 2010 Hilton Atlanta Atlanta, GA, Hotel, USA: 340-345.

[5]Xu Linfeng, Rong X, Li F, et al. Modeling and state estimation for dynamic systems with linear equality constraints[J]. IEEE Transactions on Signal Processing， 2013, 61(11): 2927-2939.

[6]劉杰. 附等式約束的卡爾曼濾波算法研究與應用[D]. 長沙： 中南大學， 2011.

Liu J. A study of Kalman Filtering Algorithm with Equality Constraints and Its Application [D]. Changsha: Central South University, 2011.

[7]褚東升, 張征. 一類帶乘性噪聲非線性系統的估計算法研究[D]. 青島： 中國海洋大學， 2006.

Chu D S, Zhang Z. Study of Estimation Algorithm for a Class of Nonlinear Systems with Multiplicative Noise [D]. Qingdao: Ocean University of Qingdao, 2006.

[8]褚東升, 尹正飛, 張玲. 基于帶乘性噪聲模型的水聲通信字符估計算法研究[J].中國海洋大學學報(自然科學版)， 2012， 42(1-2)： 149-152.

Chu D S, Yin Z F, Zhang L. Study of symbol estimation algorithm for underwater acoustic communications with multiplicative noise model [J]. Periodical of Ocean University of China, 2012, 42(1-2):149-152.

[9]褚東升, 董琦, 張玲. 帶乘性噪聲系統的傳感器故障檢測方法[J].中國海洋大學學報(自然科學版), 2013, 43(4): 112-116.

Chu D S, Dong Q, Zhang L. Study of sensor fault detection method based on systems with multiplicative noise [J]. Periodical of Ocean University of China, 2013, 43(4): 112-116.

[10]王炯琦, 矯媛媛, 周海銀, 潘曉剛. 適合處理乘性噪聲估計衛星姿態的非線性迭代濾波算法[J]. 電子學報, 2011, 39(6)： 1417-1422.

Wang J Q, Jiao Y Y, Zhou Y H, Pan X G. An iterative filter for nonlinear satellite attitude determination system with multiplicative stochastic matrix [J]. Acta Electronica Sinica, 2011, 39(6): 1417-1422.

責任編輯陳呈超

Filtering Algorithm for Nonlinear Systems with Equation State Constraints and Multiplicative Noise

WANG Chang-Sheng， ZHANG Ling， ZANG Ai-Yun, WANG Kun

(College of Engineering, Ocean University of China, The Key Laboratory of Marine Mechanical and Electrical Equipment & Instruments of Shandong Provincial Universities, Qingdao 266100, China)

With the development of controlling theory and computers, the filtering for nonlinear systems has been widely used in some areas. This paper figures out a flitering algorithm for a kind of nonlinear system with equality state constraints and multiplicative noise. By changing the state equation and observation equations based on taylor formula, a new model of linear system with equation constraints and multiplicative noise can be obtained correspondingly. The dimension of the measurement equation is augmented by perfect measurements, and the filering algorithm is derived based on the projection throrem. At last, the simulation results show the effectiveness of the proposed algorithms.

multiplicative noise; equation state constraints; nonlinear filtering; projection theorem; perfect measurements

國家自然科學基金項目(51279185,41506114)；留學回國人員科研啟動基金項目([2015]1098)；青島市博士后研究人員應用研究項目資助

2014-11-12；

2015-06-10

王昌盛(1989-)，男，碩士生。主要研究方向：智能控制與智能信息處理。E-mail：wcswang@qq.com

TN929.3

A

1672-5174(2016)08-137-04

10.16441/j.cnki.hdxb.20140339

Supported by the National Natural Science Foundation of China(51279158,41506114),the Scientific Research Foundation for Returned Overseas([2015]1098), the Applied Research Projectfor Postdoctorof Qingdao.