基于EMD-分形理論的短期電力負荷預測

關學忠，佟 宇，高 哲，聶品磊，皇甫旭

（1．東北石油大學 電氣信息工程學院，黑龍江 大慶　163318；2.遼寧大學 輕型產業學院 遼寧 沈陽 110036；3.中海油能源發展股份有限公司安全環保分公司 天津　300000）

基于EMD-分形理論的短期電力負荷預測

關學忠1，佟 宇1，高 哲2，聶品磊3，皇甫旭1

（1．東北石油大學 電氣信息工程學院，黑龍江 大慶163318；2.遼寧大學 輕型產業學院 遼寧 沈陽 110036；3.中海油能源發展股份有限公司安全環保分公司 天津300000）

電力負荷預測是電力系統規劃的重要組成部分。為了使電力系統安全經濟平穩的運行，由此特別需要精確的電力負荷預測方法。為了實現更好負荷預測方法，文中將經驗模態分解（EMD）與新興的電力負荷預測模型分形理論相結合，提出了EMD-分形負荷預測模型。為了證明此方法的有效性，文中將這種新的預測模型跟分形預測模型和BP神經網絡預測模型相比較。最終通過仿真算例說明了本文提出的這種新型預測方法精度更高，幾乎所有的誤差都在2%以下，預測結果更好，可以很好的應用在電力系統負荷預測中。

負荷預測；分形理論；經驗模態分解；EMD-分形

電力系統負荷預測是根據電力負荷、經濟、社會、氣象等的歷史數據，探索電力負荷歷史數據變化規律對未來負荷的影響，尋求電力負荷與各種相關因素之間的內在聯系，從而對未來的電力負荷進行科學的預測[1]。很多新的理論和新的技術不斷的更新也推動著負荷預測的發展，很多新的負荷預測的方法層出不窮。文獻[2]提出將負荷預測技術分為傳統預測方法、現代預測方法、經典預測方法、和組合預測方法。傳統的方法總是存在這樣那樣的弊端。

早在1975年，分形這個專有名詞是由曼德勃羅特教授首次提出，分形的早先本身的含義是不規則且支離破碎的物體[3]。以不可微、不光滑的幾何圖形為主要研究對象是分形幾何學所主要研究的內容。自然界本質正是粗糙性和非對稱性，這正是分形幾何學所主要描繪的內容。

經驗模態分解方法（Empirical Mode Decomposition，EMD）是1995年由Huang提出的一種新的信號處理方法[4]。Huang在1999年又將此方法進行了一些改進[5]。EMD分解方法從本質上來說就是對信號進行平穩化的處理，逐級的將分解信號中不同尺度的趨勢或者波動，產生出很多具有不同特征尺度的數據序列。這樣所得的每一個可以符合條件的序列稱作一個本征模函數（intrinsic mode function，IMF）分量。測試結果顯示，截止到目前為止，EMD這種方法是提取數據序列趨勢或者均值的最好的方法。

1　EMD-分形理論算法原理

1.1經驗模態分解法

任何事物的運動、變化、狀態都會產生伴隨信號，這就意味著信號在現實生活中和自然界當中是普遍存在的。信號本身表示為信息的表現形式和信息的載體，信號分析表示為對信號基本形式的表征和研究。通過對信號的分析從而揭示出信號的結構特征，這種信號分析可以有效地獲取、傳遞和處理信息。電力負荷是具有非線性、周期性、非平穩和非線性的信號。通過長時間的對電力負荷歷史數據的分析可知，電力負荷主要是由負荷分量、異常或特殊事件負荷分量、隨機負荷分量和天氣敏感分量幾個方面構成的。電力負荷可分為4類不同的分量，這4種分量受到不同種類因素的干擾影響，因此具有不同種類的變化規律。由此，文中采用將負荷分解，分解之后得到各個負荷分量，再將各個負荷分量分別預測，從而來提高負荷的預測精度。這種方法不是直接對原始的負荷進行直接預測，而是先對歷史負荷序列的數據進行處理，之后分別對上述討論的負荷所包含的其他分量一一進行單獨預測。將各個分量預測之后，再將所得的各個分量相加求和，從而來得到最終提高精度的負荷預測結果。結合上述電力系統負荷的一些特點，由此EMD分解來進行電力系統負荷的分解及其預測。

1.2分形插值算法

存在確定的數據集{（xi，yi）:i=0，1，…，M}，這個數據集的吸引子A是內插連續函數F:[x0，xM]→R的圖像，下面構造R2上的一個IFS。

IFS{R2；ωm，m=1，2，…，M}，其中ωm是式（1）的仿射變換：

使得bm=0的原因是為了使得與小區間的函數不交叉，這樣的結果會令變換后的垂直西那段與原垂直線段相同。

上述結果表示在大區間的左右端點分別映射到子區間的左右端點，所以每個變換都要滿足下面的方程：

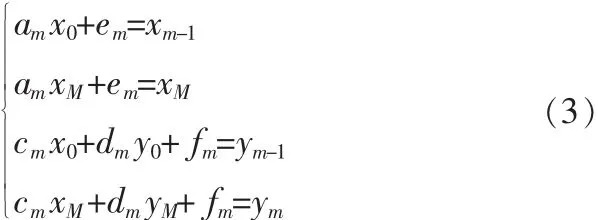
上式共有4個方程和5個參數，其中存在一個自由參數。ωm的垂直比例因子是dm[7]，這時可以將dm選擇為自由變量。令|dm|<1，這樣做的目的是使IFS收斂。令K=xM-x0，可得出下面的表達式：

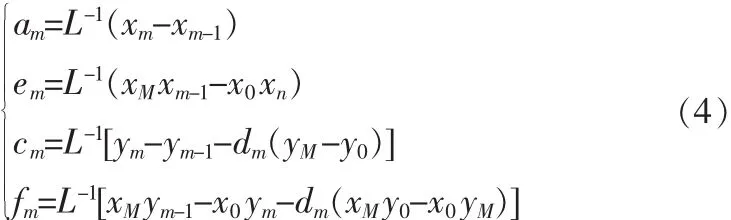
其中IFS的第i個仿射變換可由上述式子得到的參數來確定。IFS的吸引子可通過IFS的各個參數求得。之后經過多次的迭代就可得到一條穩定的插值曲線。傳統插值法反映不出兩個相鄰的信息點之間的局部特征，分形插值可以很好的解決。原來被采樣曲線的大部分特征通過插值曲線得到了保留。

電力負荷序列中的那些隨機成分經常會對負荷的預測造成很大的影響。于是，文中利用之前討論過的經驗模態分解對原負荷序列的高頻隨機分量提取出來，然后分別對分量進行建模預測。對原始負荷序列進行分解所得到的趨勢分量、隨機分量和周期分量后，利用分形預測模型分別對所得到的分量進行預測，然后將各個分量預測的結果進行相加，最后得到最終的預測結果。

綜上所述EMD-分形理論算法的實現過程如圖1所示。

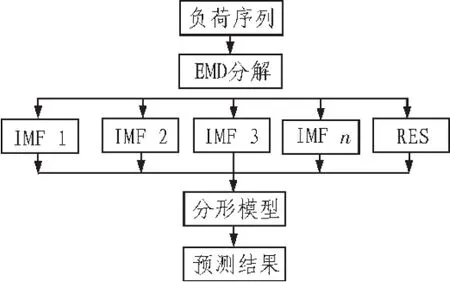
圖1　基于EMD-分形短期負荷預測模型Fig.1　Short-term load forecasting based on fractal empirical mode decomposition theory model

2　基于EMD-分形的短期電力系統負荷預測

前面已經重點研究了EMD的分解原理和算法。對比目前常用的短期電力負荷預測方法進行對比研究之后，提出一種基于EMD分形理論的短期電力負荷預測方法。針對負荷序列的隨機性、周期性、不平穩等特點，先將負荷序列進行經驗模態（EMD）分解，得到IMF分量，再將各個分量分別進行分形預測，最終將各分量預測結果進行相加。

負荷預測的數據是很龐大的，本文只列出北方某地區部分時間的歷史負荷數據。首先隨機選取我國北方某地區2009 年5月1日至2009年6月份連續50天的整點歷史負荷數據作為原始數據。該時段內的負荷曲線如圖2中（a）所示。

圖2為上述時段負荷序列的EMD分解結果，對圖2中的各個圖分別進行觀察，可以清晰的表現出EMD分解的規律性。

如圖 2所示，（a）是原始負荷序列；（b）至（g）為 IMF分量，（h）為余量。分析圖2中的各個圖像的規律，可從中看出（b）、（c）、（d）所示的IMF分量頻率很高，并且不具有明顯的周期性，認為它們是負荷序列中的高頻分量，也就是負荷序列中的隨機分量；（e）和 （f）中的IMF所呈現出一定的周期性，并且幅值很大，所以判定它們為電力系統原負荷序列的周期分量，這種周期分量與氣候相關。（g）中的IMF分量具有較強的趨勢變化特征，隨著時間的增加幅值也慢慢變大，將這個分量劃為原負荷序列的趨勢分量。最后的（h）曲線是趨勢分量的余量。

將上述分析的各個IMF負荷分量分別進行分形預測之后，將它們的各個預測值相加，就能得到最終的預測結果。因為之前所預測的數據量正如由圖2中（a）那樣較大無法直觀的觀察出預測結果的好壞，文中隨機截取2009年5月28日一天24個點進行觀察，并用BP神經網絡預測同一天的負荷，從而達到對比的目的。結果圖對比如圖3。

圖2　EMD負荷序列分解結果Fig.2　The result of EMD load sequence decomposition

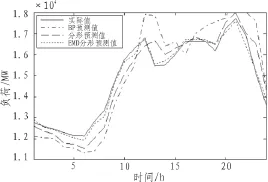
圖3　三種預測模型和實際值的比較Fig.3　Comparison of three forecasting models and actual values

3　結　論

圖3是3種預測模型的預測值與實際值的對比圖。由圖3可清晰看到，分形預測和實際值的匹配度要比BP神經網絡[8-10]模型要好，基本上和實際值沒有多大區別，但是利用EMD-分形模型的預測值實際值的匹配度更高，是三者當中最好的。BP神經網絡預測模型的預測結果比其他兩種預測模型的預測結果要稍差。它的變化趨勢與實際情況的變化趨勢在一定程度上還是有差別的。表1是2008年5月28日，3種預測模型的24個小時整點負荷預測結果。從表1中可以看出，分形預測模型的預測誤差比較低，比BP神經網絡預測模型的預測誤差要小，但是也有很多相對誤差大于5%。而EMD-分形預測模型要比其他兩種模型預測預測誤差都要小，是3種模型當中預測誤差最小的，幾乎所有的誤差都在2%以下。算例結果說明，EMD-分形預測模型可以很好的對電力負荷進行預測，這種預測模型有較強的實用性。

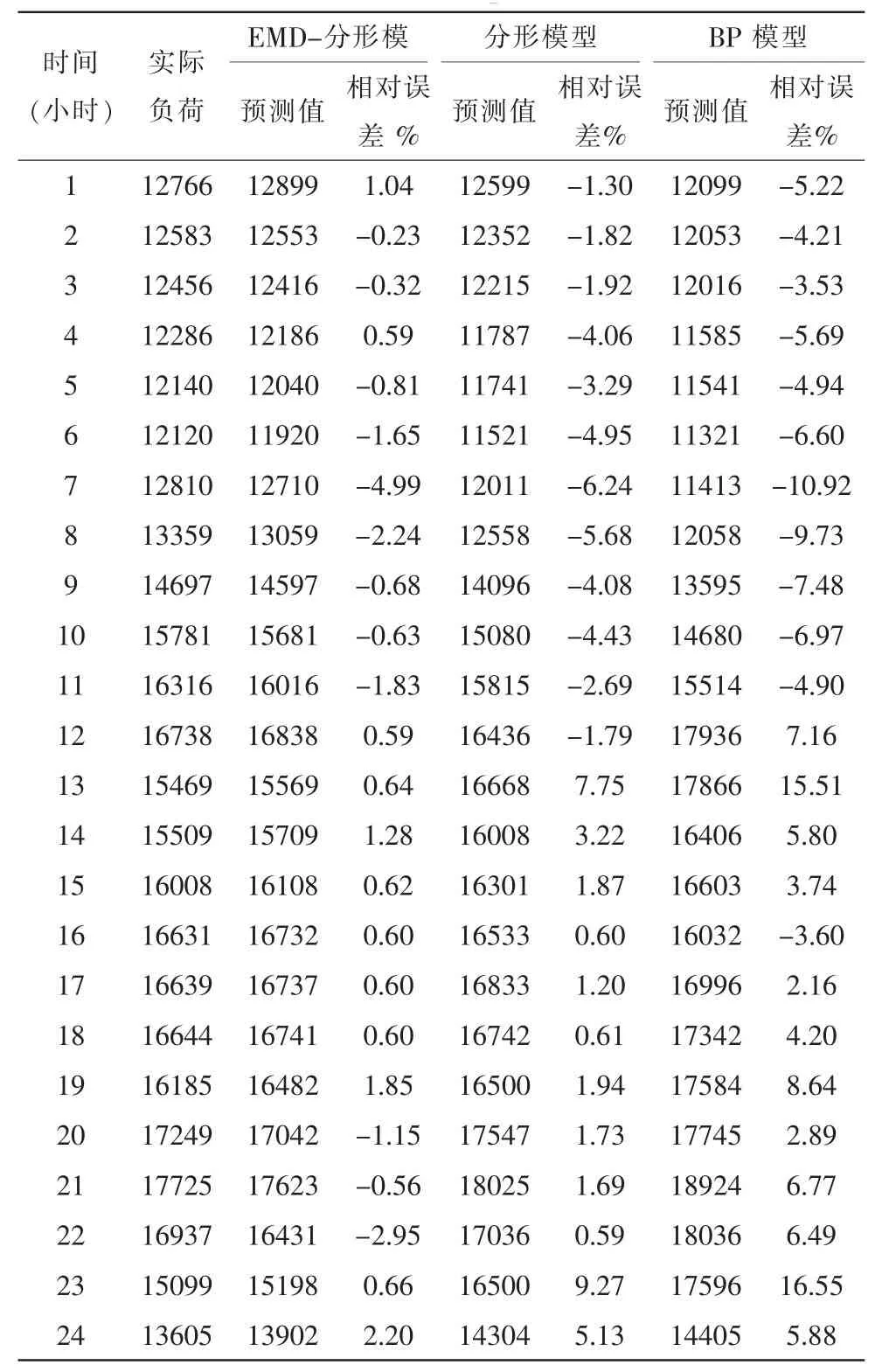
表1　三種模型預測值Tab.1　Three models predicted value

[1]康重慶，夏清，劉梅.電力系統負荷預測[M].北京:中國電力出版社，2007.

[2]Neill-Carrillo E O，Heydt G T，Kostelieh E J.Chaotic phenomena in power Systems:Detection and APPlications. Electric Machines and Power Systems，1999（27）:79-91.

[3]喬艷芬.基于分形理論的電力負荷特性研究及預測[D].北京：華北電力大學（北京）2006.

[4]Huang N.E，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis.Proc.R.Soc.Lond.A.1998.

[5]Huang N E，Shen Z，Long S.R.A new view of nonlinear water waves:the Hilbert spectrum[M].Ann Rev Fluid Mech，1999

[6]Bansley M F.Fractals Everywhere（Second Edition）[M]. Academic Press，1993.

[7]唐立春，李光熹，熊曼麗.基于分形的電力系統負荷預測[J].電力系統及其自動化學報，1999，11（4）:21-24.

[8]金文志.基于改進BP網絡的甲烷傳感器溫度影響試驗研究[J].電子設計工程，2015（7）:15-17.

[9]蘇宇逍.基于GA的BP神經網絡在多目標優化中的應用[J].電子科技，2015（6）:51-53.

[10]李志峰，張二艷.BP神經網絡在空氣質量評價分級中的探索與應用[J].電子技術與軟件工程，2014（5）:43-44.

Short-term power load forecasting based on fractal Empirical Mode Decomposition theory

GUAN Xue-zhong1，TONG Yu1，GAO Zhe2，NIE Pin-lei1，HUANGFU Xu1
（1．College of Electrical and Information Engineering，Northeast Petroleum University，Daqing 163318，China；2．College of Light Industry，Liaoning University，Shenyang 110036，China；3．CNOOC Energy Technology&Services Limited，Tianjin 300000，China）

Power load forecasting is an important part of power system.To make the power system stability，therefore special needs accurate load forecasting method.In this paper，in order to achieve a better load forecasting mode，combine the Empirical Mode Decomposition（EMD）and fractal theory and improve the EMD fractal load forecasting model.In order to prove the effectiveness of this method，the paper use this new forecasting model compared with fractal forecasting model and BP neural network forecasting model.Finally the simulate example illustrates this new forecasting method proposed higher precision and better forecasting.Almost all of the errors are below 2%.The result proved it can be a good application in electric power system load forecasting.

load forecasting；fractal theory；empirical mode decomposition；EMD-fractal

TN0

A

1674－6236（2016）01-0184-03

2015-05-15稿件編號：201505132

國家自然科學基金（61304094）

關學忠（1962—），男，吉林蛟河人，博士，教授。研究方向：智能控制，模糊控制，嵌入式系統。