基于發電機響應的切機控制算法研究

胡雪凱，劉翔宇，張　乾，戎士洋

（1.國網河北省電力公司電力科學研究院，石家莊 050021；2.國網河北省電力公司檢修分公司，石家莊 050070）

基于發電機響應的切機控制算法研究

胡雪凱1，劉翔宇1，張乾2，戎士洋1

（1.國網河北省電力公司電力科學研究院，石家莊 050021；2.國網河北省電力公司檢修分公司，石家莊 050070）

提出了一種基于發電機響應的電力系統切機控制方法，與以往緊急控制方案不同，該方法不依賴于預想故障，而是根據實測的發電機信息進行切機量的計算和控制地點的選擇，從而制訂切機控制措施。以實際電網為例驗證所提方法的有效性。

電力系統；發電機響應；切機控制；失穩裕度

0　引言

緊急控制研究的物理意義為，對提高電力系統暫態穩定性這一控制目標如何給出最佳的控制量，主要流派之一是基于Lyapunov穩定性理論的直接法與薛禹勝院士提出的擴展等面積準則（EEAC）［1］。與直接法相比，EEAC能夠處理任意復雜的電力系統數學模型，這種對模型的強適應性是直接法所不具備的［2-5］。

然而，目前的大多切機控制算法存在一定的局限性，或是過于依賴預想運行方式和故障集，或是選取的控制條件沒有充分考慮到電力系統的運動學規律［6-8］。隨著WAMS在電力系統的應用，現在已經能夠實時獲取故障后各機組的功角、角速度、功率等實時響應曲線，為緊急切機控制提供了數據基礎。

基于發電機的實時響應信息，首先對電力系統的運動學規律方程進行討論分析；其次，以該方程為基礎，導出了切機所需要的第1個控制量——切機量的計算方法；最后，結合失穩裕度，導出了切機所需要的第2個控制量——控制地點的計算方法，進而得出最終的切機控制算法。

1　切機量的隱函數形式

設切機操作完成時刻為Tec，與判別失穩時刻Te相比，Tec中還應包含切機控制的動作時間延時Td，即Tec=Te+Td，對應的等值OMIB系統的功角為δec。采取緊急控制時的等面積準則示意見圖1。

為計算切機控制量，還需假設采取切機控制后，電磁輸出功率PPFe的時變參數Pc、A、B定常，并取為Te時刻對應的數值。

該假設會使計算結果出現一些誤差，但由于最終實施的切機控制是一接近計算結果且比計算結果大的離散量，這在一定程度上可以減小計算結果的誤差。

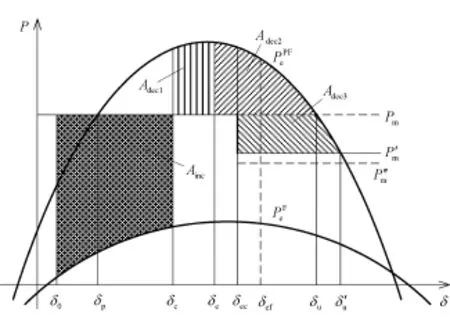
圖1　采取緊急控制時的等面積準則

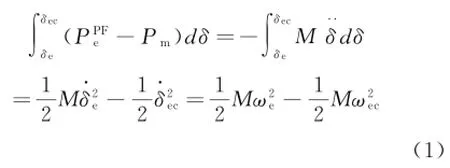
式中：PPFe為切機控制后的電磁輸出功率；Pm為切機前的機械輸入功率；M為系統的等值慣性常數；δ為對應時刻的功角。

所以，在Tec時刻系統的剩余動能為：

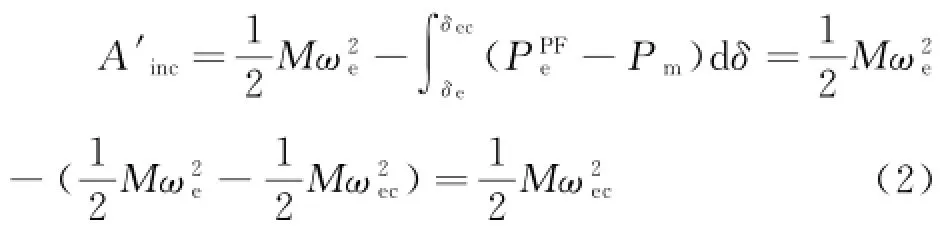
考慮到切機控制也切除了一部分剩余動能，因此，系統中的剩余動能最終變為：

而在Tec時刻系統的動能減速面積將變為：

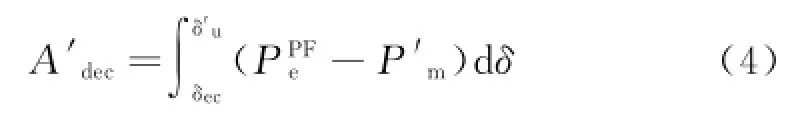
由圖1可知，為保證系統的穩定，需A'dec≥A'inc，即切機控制量的隱函數形式為：

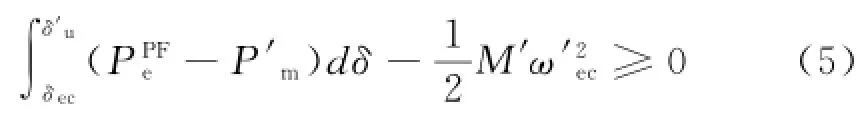
考慮到上述假設后，式（5）最終可表達為：

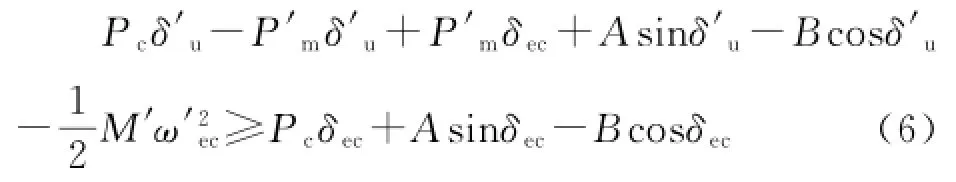
2　快速切機量計算

式（6）中有一個未知量δ'u，由圖1可知：

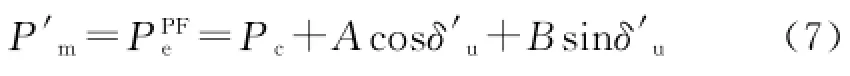
由式（7）可解出：

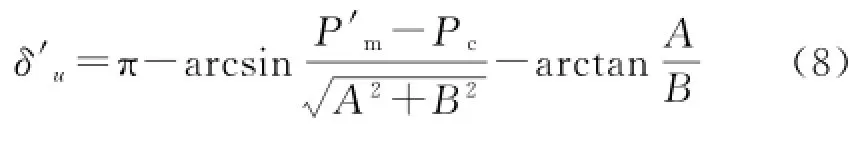
需要說明的是，式（6）中的4個未知量P'm、δ'u、M'、ω'ec都是與被切除的發電機有關的量，一旦被切除的發電機確定，即控制地點選定后，可立即計算出M'和ω'ec。再由式（8）可知，δ'u與P'm相關，為了求出P'm，需通過迭代的方法。然而，由于迭代計算較耗時，所以不適于實時控制。考慮到等值后的實際被切機組容量需大于或等于切機控制量（Pm-P'm）且離它最接近，即需遵循“寧多切，勿不足”的切機原則，因此，當可被切除的發電機按受擾程度排序后，可逐次遞加切除，直到滿足式（6）為止。這種算法雖然可行，但對實時控制而言仍然較慢。

為了快速制訂切機控制規律，可先作如下2個近似以得到初始的切機控制規律：切機控制后，慣性常數Ms、MT不變，剩余動能不變，即仍為；切機控制后，等值OMIB系統的不穩定平衡點不變，即仍為δu，這相當于忽略了圖1中從δu到δ'u的近似三角形的動能減速面積。

基于這2個近似，并令A'dec≥A'inc，則式（6）可表達為：

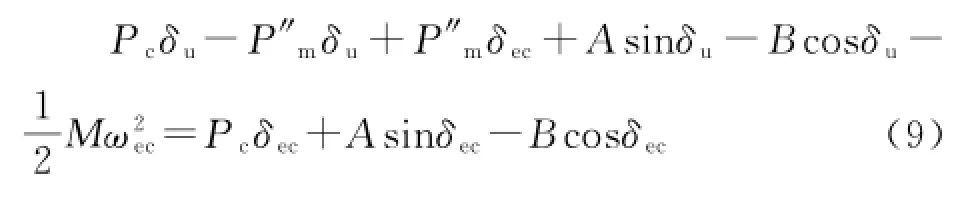
由式（9）可得切機控制后等值OMIB系統的近似機械輸入功率P″m為：

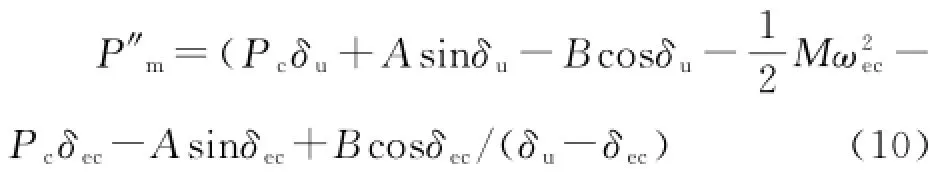
由等值OMIB系統的可得歸算到多機系統的總切機量為：

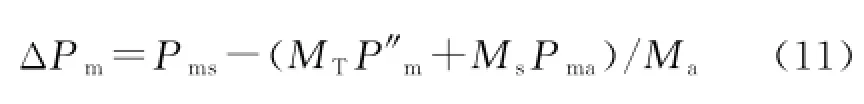
3　控制地點的選擇

在系統判別失穩時刻第i臺發電機的剩余動能為：

式中：ω~ie為Te時刻第i臺發電機在慣性中心坐標下的轉速。

而此時第i臺發電機尚可吸收的動能為：

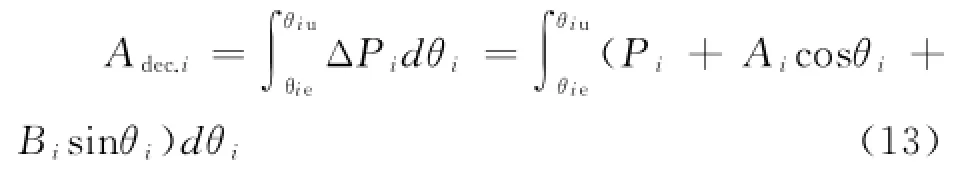
式中：θie為Te時刻第i臺發電機在慣性中心坐標下的轉角；θiu為慣性中心坐標下第i臺發電機的不穩定平衡點。

假設Te時刻后第i臺發電機為單機自治系統，即不平衡功率ΔPi的時變參數Pi、Ai、Bi定常，并取為Te時刻對應的數值，則由式（13）可計算出動能減速面積為：

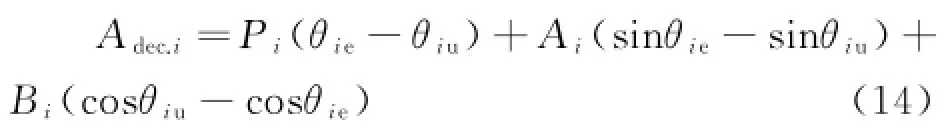
如果Ainc.i＞Adec.i，則表示第i臺發電機相對于慣性中心失穩，定義失穩裕度為：

并取S中所有ηi＞0的發電機全體組成主動失穩機群，記為：

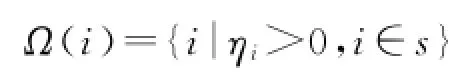
為尋找具有控制負效應的發電機，需逐次切除主動失穩機群中的一臺發電機以觀察等值OMIB系統機械輸入功率P'm的變化。當Ω（i）中的第i臺發電機被切除時，P'm為：

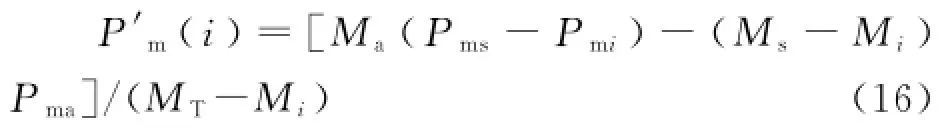
如果P'm（i）＞Pm，則第i臺發電機為具有控制負效應的發電機，應該從主動失穩機群中除去這臺發電機。因此，除去具有控制負效應的發電機后的主動失穩機群可記為：Ω'（i）=｛i|ηi＞0且P'm（i）≤Pm，i∈s｝將Ω'（i）中的所有發電機按照ηi從大到小的順序進行排序便可得到考慮控制負效應的發電機受擾程度排序表。當初始切機控制量ΔPm確定后，可取總容量大于ΔPm且最接近于ΔPm的發電機受擾程度排序表中的前幾臺發電機作為初始切機控制規律，再以初始切機控制規律為初值通過迭代求取最終的切機控制規律。

4　算例分析

下面以某實際電網為例，驗證所提切機控制方法的有效性。0 s時發生三相短路故障，0.23 s切除。各機相對慣性中心的功角曲線及分群結果見圖2，等值系統軌跡見圖3。

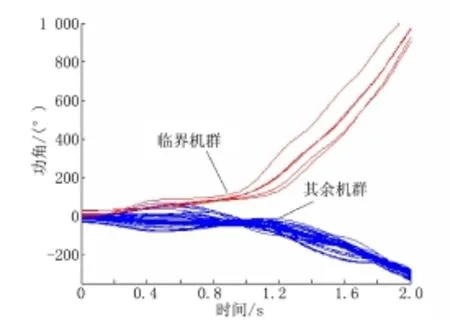
圖2　功角曲線及分群結果

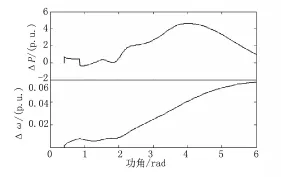
圖3　等值系統軌跡

判斷出系統失穩的時刻為0.35 s，此時開始進行切機控制的計算。

根據前面的控制策略，計算出切機量近似為ΔP=1.43，臨界機群中的各機組都是不具有控制負效應的主動失穩機群，它們的失穩裕度和有功功率如表1（按失穩裕度排序）。結合前面計算出的切機量可得到控制策略為切除機組G61、G62、G49。

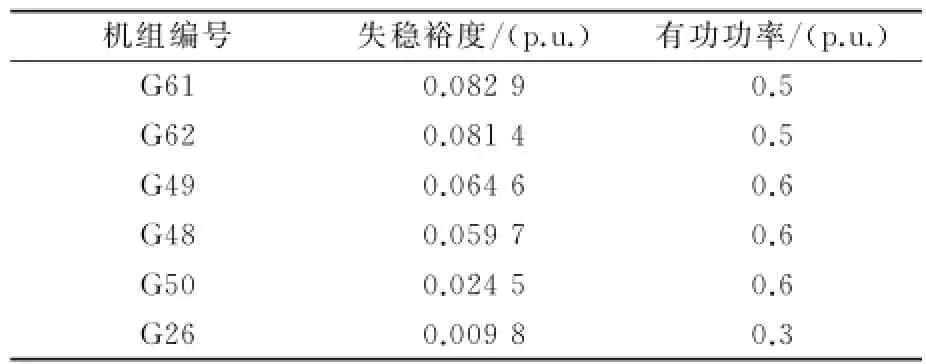
表1　臨界機群的失穩裕度和有功功率

考慮到命令傳輸及切機延時后，假設0.4 s時控制子站完成切機操作，切機后各機相對慣性中心的功角曲線及分群結果如圖4。切機后的等值軌跡如圖5。

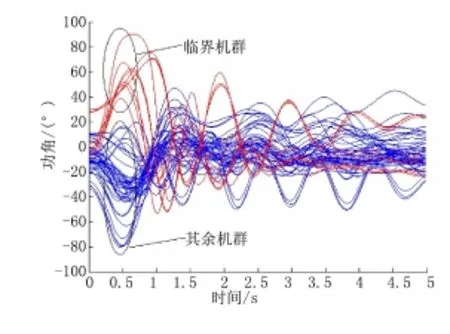
圖4　切機后各機相對慣性中心的功角曲線及分群結果

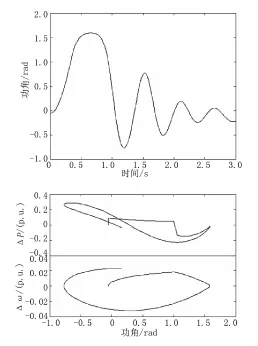
圖5　切機后的等值系統軌跡

從等值軌跡曲線和相平面曲線都能看出，采取控制措施后系統重新回到了穩定運行狀態，即提出的切機控制方法有效地阻止了系統穩定性的惡化。

5　結束語

基于WAMS實時測量的發電機響應信息，提出了一種基于EEAC理論的緊急切機控制算法。其具體執行步驟為：

a.近似計算出切機控制量；

b.計算慣性中心坐標下各機的失穩裕度；

c.將各機失穩裕度從大到小排序，去除其中具有控制負效應的機組，得到發電機受擾程度排序表；

d.取總容量大于ΔPm且最接近于ΔPm的受擾程度排序表中的前幾臺發電機作為切機控制策略。

［1］ 薛禹勝.運動穩定性量化理論-非自治非線性多剛體系統的穩定性分析［M］.南京：江蘇科學技術出版社.

［2］ 薛禹勝.EEAC與直接法的機理比較（一）受擾程度函數［J］.電力系統自動化，2001，25（11）：6-11.

［3］ 薛禹勝.EEAC與直接法的機理比較（二）壁壘點與觀察點［J］.電力系統自動化，2001，25（12）：1-7.

［4］ 薛禹勝.EEAC與直接法的機理比較（三）定性判穩與定量分析［J］.電力系統自動化，2001，25（13）：1-5.

［5］ 薛禹勝.EEAC與直接法的機理比較（四）回顧與前瞻［J］.電力系統自動化，2001，25（14）：1-6.

［6］ 畢兆東，王建全，韓禎祥.基于數值積分法靈敏度的快速切負荷算法［J］.電網技術，2002，26（8）：4-7.

［7］ 彭疆南.基于能量整形的電力系統暫態穩定控制設計研究［D］.北京：清華大學，2004.

［8］ 方勇杰，范文濤，陳永紅，等.在線預決策的暫態穩定控制系統［J］.電力系統自動化，1999，23（1）：8-11.

本文責任編輯：齊勝濤

Research on Generator-tripping Control Based on Generator Response

Hu Xuekai1，Liu xiangyu1，Zhang Qian2，Rong Shiyang1
（1.State Grid Hebei Electric Power Corporation Technology Research Institute，Shijiazhuang 050021，China；2.State Grid Hebei Electric Power Corporation Maintenance Branch，Shijiazhuang 050070，China）

This paper proposes a generator-tripping control scheme based on the response of generator.Different from early emergency control method，it doesn't depend on expected failure.With the real-time measured information，calculate the generator tripping quantity.Then obtains the sorting table based on the disturbed degree of every generator，removing the generators which have negative control effect，the generator-tripping control scheme can be formulated.

power system；generator response；generator-tripping control；disturbed degree

TM301.2

A

1001-9898（2016）02-0022-04

2015-11-12

胡雪凱（1987-），男，工程師，主要從事電力系統分析和電能質量測試等工作。