長方形的大用處
2016-09-10 07:22:44徐延榮
數學大王·中高年級 2016年2期
徐延榮
有些應用題的相關數量的積是具有實際意義的,比如,速度×時間=路程,工作效率×時間=工作總量,單價×數量=總價,平均分×人數=總分,等等。對于這類應用題,我們可以借助長方形圖形來解答。
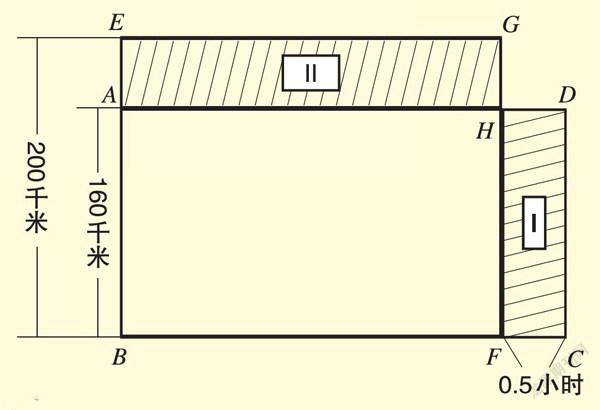
攔路虎一:特快列車正常是以每小時160千米的速度從甲地開往乙地,現在如果把速度提高到每小時200千米,那么特快列車從甲地到乙地所需時間可以縮短30分鐘,請問甲地到乙地有多遠?
【奇思妙解】如果用長方形的長表示時間,寬表示速度,則其面積就表示路程,那么題意可如下圖所示。
由于長方形ABCD和長方形EBFG的面積都表示甲地到乙地的路程,所以兩個陰影長方形的面積相等。陰影I的面積=160×0.5=80,則陰影II的長AH=80÷(200-160)=2,故長方形EBFG的面積=200×2=400,可知甲乙兩地之間的路程為400千米。
攔路虎二:一個學習小組有12個同學。一次數學測驗,李平請了病假,11個同學的平均分是85分。李平補考的成績比12個同學的平均分還高5.5分,請問李平考了多少分?
【奇思妙解】如果用長方形的長表示人數,寬表示平均分,則其面積表示總分,那么題意可如下圖所示。

由于長方形ABCD和長方形EBFG的面積分別表示11人和12人的總分,所以陰影部分的面積就表示李平的分數,而長方形CFGH表示12人的平均分,那么長方形EADH的面積就表示李平比12人的平均分高出的分數,即5.5分,則EA = 5.5÷11=0.5,12人的平均分EB=85+0.5=85.5,所以李平的成績為85.5+5.5=91(分)。

