海上作業(yè)起重機(jī)主動(dòng)升沉補(bǔ)償系統(tǒng)的設(shè)計(jì)與分析
吳金波 宋宇宸
華中科技大學(xué),武漢,430074
?
海上作業(yè)起重機(jī)主動(dòng)升沉補(bǔ)償系統(tǒng)的設(shè)計(jì)與分析
吳金波宋宇宸
華中科技大學(xué),武漢,430074
為補(bǔ)償船用起重機(jī)在海上作業(yè)時(shí)的升沉運(yùn)動(dòng),構(gòu)造了基于二次調(diào)節(jié)靜液傳動(dòng)技術(shù)的絞車液壓驅(qū)動(dòng)系統(tǒng)。首先,建立了升沉補(bǔ)償系統(tǒng)的完整數(shù)學(xué)模型,提出了包含二次單元變量油缸位置環(huán)、二次單元馬達(dá)速度環(huán)及二次單元馬達(dá)位置環(huán)的三閉環(huán)控制結(jié)構(gòu)。然后,給出了三閉環(huán)控制器的設(shè)計(jì)方法,為了得到起重機(jī)貨物的位移,利用鋼絲繩張力設(shè)計(jì)了狀態(tài)觀測器。最后,給出了一個(gè)設(shè)計(jì)實(shí)例,通過數(shù)字仿真從頻域角度分析了升沉補(bǔ)償系統(tǒng)的動(dòng)態(tài)特性,為控制策略的研究打下基礎(chǔ)。
主動(dòng)升沉補(bǔ)償;二次控制單元;海上作業(yè);動(dòng)態(tài)特性;海洋技術(shù)
0 引言
海上作業(yè)起重機(jī)屬于重要的海洋工程裝備,對于保障高海況下的作業(yè)效率和作業(yè)安全具有重要意義。國際上少數(shù)幾個(gè)海洋技術(shù)發(fā)達(dá)的國家已掌握了主動(dòng)波浪補(bǔ)償起重機(jī)的核心技術(shù),而我國在這方面的研究起步較晚,研究成果甚少,正處于發(fā)展階段。升沉補(bǔ)償系統(tǒng)按動(dòng)力供應(yīng)的不同可分為被動(dòng)型、主動(dòng)型和半主動(dòng)型[1]。被動(dòng)升沉補(bǔ)償系統(tǒng)依靠蓄能器吸收母船升沉的能量,不需外界提供能量,但存在補(bǔ)償精度低、補(bǔ)償性能不穩(wěn)定、滯后嚴(yán)重等問題[2];主動(dòng)升沉補(bǔ)償系統(tǒng)利用慣導(dǎo)、張力傳感器等構(gòu)成閉環(huán)反饋控制,補(bǔ)償精度高,抗干擾能力強(qiáng),性能穩(wěn)定,但是消耗的功率大[3-4];半主動(dòng)升沉補(bǔ)償系統(tǒng)兼具主被動(dòng)升沉補(bǔ)償?shù)奶攸c(diǎn),但也存在適應(yīng)性差、補(bǔ)償位移有限等缺點(diǎn)[5]。從升沉補(bǔ)償系統(tǒng)的驅(qū)動(dòng)方式來看,主要分為旋轉(zhuǎn)型升沉補(bǔ)償裝置和直線型升沉補(bǔ)償裝置,相比較而言,后者需要復(fù)雜的油缸與滑輪組,且受限于液壓缸的行程,不能滿足惡劣海況下的升沉補(bǔ)償要求。
本文利用靜液二次調(diào)節(jié)技術(shù),設(shè)計(jì)了絞車形式的旋轉(zhuǎn)型升沉補(bǔ)償裝置。以德國力士樂公司生產(chǎn)的專門針對主動(dòng)式升沉補(bǔ)償系統(tǒng)的二次控制單元為主要研究對象[6],建立了升沉補(bǔ)償系統(tǒng)的完整數(shù)學(xué)模型,并將電力拖動(dòng)系統(tǒng)中的多閉環(huán)思想引入升沉補(bǔ)償控制系統(tǒng)中,構(gòu)造了包含三個(gè)閉環(huán)的控制結(jié)構(gòu),從頻域角度分析其動(dòng)態(tài)特性,并給出了三個(gè)控制器的設(shè)計(jì)方法。為得到起重機(jī)貨物的升沉位移,本文還構(gòu)造了基于鋼絲繩張力檢測的狀態(tài)觀測器,充分考慮了物理上實(shí)現(xiàn)的可行性。
1 系統(tǒng)組成及工作原理
二次調(diào)節(jié)技術(shù)是指一個(gè)或一組帶壓力耦聯(lián)的執(zhí)行器工作于恒壓網(wǎng)絡(luò)中,并可實(shí)現(xiàn)能量回收與再利用的靜液驅(qū)動(dòng)技術(shù)[7]。二次調(diào)節(jié)單元的一端與高壓的恒壓源連接, 另一端與低壓的恒壓源連接,使其壓差基本恒定不變,建立其排量與其負(fù)載成比例的關(guān)系。二次調(diào)節(jié)中的二次元件(液壓變量馬達(dá)/泵)是通過改變液壓馬達(dá)/泵的排量來調(diào)節(jié)輸出轉(zhuǎn)矩或轉(zhuǎn)速的。以力士樂公司生產(chǎn)的A4VSO DS2二次控制單元為例,二次元件能工作在四個(gè)象限內(nèi),既有“泵”工況的雙向,也有“馬達(dá)”工況的雙向。當(dāng)二次控制單元的排量大于負(fù)載的需求時(shí),為馬達(dá)工況,驅(qū)動(dòng)起重機(jī)貨物上升,能源消耗;當(dāng)二次控制單元的排量少于負(fù)載的需求時(shí),為泵工況,被起重機(jī)貨物拖動(dòng)下降,能源回收到蓄能器內(nèi),以達(dá)到節(jié)約能源的目的。蓄能器的作用不僅在于能存儲(chǔ)或釋放能源,而且能在瞬間切換時(shí)補(bǔ)充流量的需求以避免出現(xiàn)真空現(xiàn)象。
如圖1所示,起重機(jī)絞車液壓驅(qū)動(dòng)系統(tǒng)主要由二次控制單元和恒壓源組成。恒壓源包括恒壓變量泵、蓄能器及相關(guān)附件。二次控制單元?jiǎng)t包括電液伺服閥、對稱雙出桿變量缸、二次元件(變量馬達(dá)/泵)、二次元件控制器等。其中變量液壓缸內(nèi)置位移傳感器,和電液伺服閥、二次元件控制器構(gòu)成了一個(gè)小閉環(huán)的位置伺服系統(tǒng),該位置小閉環(huán)的輸出為變量液壓缸活塞位移,變量油缸活塞帶動(dòng)二次元件的斜盤,從而達(dá)到控制變量馬達(dá)/泵的排量的目的。

圖1 船用起重機(jī)液壓驅(qū)動(dòng)系統(tǒng)原理圖
2 數(shù)學(xué)建模
為方便推導(dǎo)出描述升沉補(bǔ)償系統(tǒng)動(dòng)態(tài)特性的數(shù)學(xué)模型,特作如下假設(shè):忽略恒壓源在工作過程中的壓力波動(dòng);不考慮起重機(jī)載荷對船體的反作用力影響;將鋼絲繩等效為彈簧-阻尼模型;變量缸活塞的初始位置選擇在使二次元件斜盤傾角為0的地方;液壓系統(tǒng)在工作過程中,溫度不發(fā)生變化。
2.1電液伺服閥
電液伺服閥通常以電流I作為輸入?yún)?shù),以電液伺服閥的輸出流量qVL作為輸出參數(shù)。在主動(dòng)升沉補(bǔ)償系統(tǒng)中,電液伺服閥的頻率響應(yīng)遠(yuǎn)大于整個(gè)系統(tǒng)的頻寬,因而伺服閥的傳遞函數(shù)可以簡化為比例環(huán)節(jié):
qVL=KVI
(1)
式中,qVL為變量控制油缸的輸入流量;KV為伺服閥流量增益。
2.2變量控制油缸
變量控制油缸以輸入流量qVL作為輸入?yún)?shù),以油缸活塞位移Y作為輸出參數(shù),如果不計(jì)干擾和摩擦力,則可得電液伺服閥的控制輸入對變量油缸活塞位移的傳遞函數(shù)[8]:
(2)
式中,A為變量控制油缸有效作用面積;Cct為控制油缸總泄漏系數(shù);Vt為伺服閥至變量油缸的總?cè)莘e;βe為工作液體的體積彈性模量;m為折算到變量控制油缸活塞的等效質(zhì)量;BP為變量控制油缸活塞及負(fù)載的黏性阻尼系數(shù);K為負(fù)載的彈簧剛度。
設(shè)變量控制機(jī)構(gòu)剛度足夠大,無彈性負(fù)載(K=0),且BPCct?A2(這是因?yàn)橛绅ば阅Σ亮σ鸬男孤┝髁克a(chǎn)生的活塞速度小得多),則式(2)可化簡為
或簡化為
(3)
(4)
式中,ωh為液壓固有頻率;ζh為液壓阻尼比;
由于變量控制油缸容積Vt很小,可不計(jì)體積壓縮變化引起的流量變化;忽略油缸泄漏,則變量控制油缸部分可以進(jìn)一步簡化為積分環(huán)節(jié):
(5)
2.3二次元件
二次元件以變量控制油缸活塞位移Y作為輸入?yún)?shù),二次元件排量V作為輸出參數(shù)。一般地,二次元件的斜盤傾角γ為10°左右[9],此范圍內(nèi)tanγ=Y/ra,所以可以用γ代替tanγ。ra為二次元件擺動(dòng)斜盤的有效半徑。變量油缸活塞位移對二次元件輸出斜盤傾角的傳遞函數(shù)為
(6)
二次元件排量方程為
(7)
式中,Vmax為二次元件的最大排量;Ymax為二次元件變量控制油缸最大位移;γmax為二次元件的最大斜盤傾角。
二次元件在進(jìn)行升沉補(bǔ)償時(shí),力矩平衡方程為
(8)
式中,Jm為絞車、減速器等折算到二次元件輸出軸的總轉(zhuǎn)動(dòng)慣量;Bm為絞車、減速器等折算到二次元件輸出軸的總黏性阻尼系數(shù);ML為負(fù)載轉(zhuǎn)矩;θm為二次元件主軸轉(zhuǎn)角;ηh為二次元件液壓效率;ps為恒壓系統(tǒng)的壓力。
2.4鋼絲繩卷繞系統(tǒng)
將鋼絲繩負(fù)載系統(tǒng)等效為彈簧-質(zhì)量-阻尼模型,將鋼絲繩的伸長量Δl分為動(dòng)態(tài)伸長量Δld和靜態(tài)伸長量Δls,令負(fù)載在垂直方向上的位移為xL,則有以下關(guān)系:
xL=xh-θmR/i+Δl
(9)
Δl=Δls+Δld
(10)
式中,xh為船舶在垂直方向上的綜合升沉位移;R為絞車滾筒的半徑;i為絞車齒輪速率比。
空氣中,被吊貨物在垂直方向的動(dòng)力學(xué)方程為
(11)
式(10)中,Δls為一常數(shù),即
(12)
根據(jù)文獻(xiàn)[10],被吊貨物的等效質(zhì)量與等效靜拉力分別為
meq=M+ml/3
(13)
(14)
式中,M為負(fù)載貨物質(zhì)量;m為鋼絲繩單位長度質(zhì)量;l為鋼絲繩長度。
2.5完整的升沉補(bǔ)償系統(tǒng)
設(shè)起重機(jī)液壓絞車由一臺(tái)二次馬達(dá)分別通過減速器進(jìn)行驅(qū)動(dòng),則針對式(8)中的參數(shù)有
Jm=Js+Jr+Jg/i2
(15)
式中,Js為二次元件輸出軸的轉(zhuǎn)動(dòng)慣量;Jr為減速器折算到輸入軸的轉(zhuǎn)動(dòng)慣量;Jg為鋼絲繩滾筒的轉(zhuǎn)動(dòng)慣量。
總黏性阻尼系數(shù)Bm為
Bm=Bsm+Br+Bg/i2
(16)
式中,Bsm為二次元件輸出軸的黏性阻尼系數(shù);Br為減速器折算到輸入軸的黏性阻尼系數(shù);Bg為鋼絲繩滾筒的黏性阻尼系數(shù)。
根據(jù)絞車和貨物間的關(guān)系,有
(17)
以Δld為系統(tǒng)狀態(tài)變量,式(3)、式(6)~式(17)即完整的船用起重機(jī)升沉補(bǔ)償系統(tǒng)的動(dòng)力學(xué)模型。
3 控制器設(shè)計(jì)
本文討論的船用起重機(jī)升沉補(bǔ)償自動(dòng)系統(tǒng)是一典型的軌跡跟蹤控制系統(tǒng)[11],需要一定的帶寬,即要有較好的動(dòng)態(tài)性能,以快速補(bǔ)償波浪對船體的綜合升沉位移(主要是指船體的橫搖、縱搖和升沉運(yùn)動(dòng)對吊鉤的影響)。
而從控制系統(tǒng)的結(jié)構(gòu)來講,可以構(gòu)成變量油缸位置環(huán)、二次元件速度環(huán)及位置環(huán)(該位置環(huán)即可從二次元件馬達(dá)角位移引出,也可由起重機(jī)貨物垂向位移引出)的三環(huán)結(jié)構(gòu),也可構(gòu)成變量油缸位置環(huán)和起重機(jī)貨物位移(或二次元件角位移)位置環(huán)的兩環(huán)結(jié)構(gòu),這和電力伺服驅(qū)動(dòng)系統(tǒng)中的位置伺服系統(tǒng)類似,由式(8)可以將變量油缸位置環(huán)類比于電力伺服驅(qū)動(dòng)系統(tǒng)中的電流環(huán),直接控制二次元件的輸出扭矩。考慮到系統(tǒng)的軌跡跟蹤控制能力,采用了三環(huán)控制結(jié)構(gòu),這是因?yàn)閮森h(huán)系統(tǒng)的速度軌跡控制能力偏弱[12]。
聯(lián)立式(3)、式(7)~式(17),并進(jìn)行相應(yīng)的拉氏變換,可得圖2所示的控制系統(tǒng)方塊圖。圖2中MRU為運(yùn)動(dòng)參考單元,用以測量船舶的縱搖、橫搖和升沉運(yùn)動(dòng);xr為規(guī)劃的軌跡指令信號;u為軌跡跟蹤控制器的輸出。
可將升沉補(bǔ)償系統(tǒng)看作一個(gè)帶位置干擾的單輸入單輸出系統(tǒng),其中,xr為系統(tǒng)輸入,xh為系統(tǒng)的外部干擾,xv為系統(tǒng)輸出。系統(tǒng)控制的目標(biāo)為:在有外界干擾的情況下,使系統(tǒng)輸出快速而準(zhǔn)確地復(fù)現(xiàn)系統(tǒng)輸入。
3.1多閉環(huán)控制器的設(shè)計(jì)
可以將電力拖動(dòng)中的多閉環(huán)位置伺服系統(tǒng)控制器的設(shè)計(jì)方法引入升沉補(bǔ)償控制系統(tǒng)中,采用從內(nèi)環(huán)到外環(huán)的設(shè)計(jì)方法,逐個(gè)設(shè)計(jì)各環(huán)的調(diào)節(jié)器。對變量油缸位置環(huán),其開環(huán)傳遞函數(shù)見式(3),含有一個(gè)積分環(huán)節(jié),是I型伺服系統(tǒng),可以采用比例控制:
G3=k3p
(18)
應(yīng)用勞斯判據(jù)得系統(tǒng)的穩(wěn)定條件為
k3pKV/A<2ζhωh
(19)
再應(yīng)用穩(wěn)定邊界法中的齊格勒-尼科爾斯公式,可推出
k3p=ζhωhA/KV
(20)
則變量油缸位置環(huán)的頻率特性及其近似式為
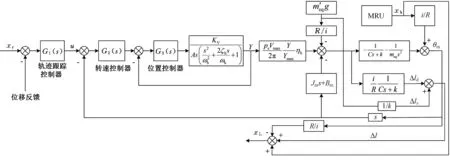
圖2 升沉補(bǔ)償控制系統(tǒng)方塊圖
上式成立的條件是
在工程計(jì)算中,一般允許有10%以內(nèi)的誤差,因此,近似條件可以寫成

(21)
在此條件下,變量油缸位置內(nèi)環(huán)的閉環(huán)傳遞函數(shù)為
(22)

(23)
鋼絲繩阻尼系數(shù)C通常較小,忽略它的影響,則式(23)的頻率特性為
同理,速度環(huán)簡化的近似條件可以寫成
(24)
為了實(shí)現(xiàn)轉(zhuǎn)速無靜差以提高軌跡跟蹤精度,在負(fù)載擾動(dòng)作用點(diǎn)前面須有一個(gè)積分環(huán)節(jié),它應(yīng)該包含在轉(zhuǎn)速調(diào)節(jié)器中。所以轉(zhuǎn)速控制器采用PI調(diào)節(jié),其傳遞函數(shù)為
(25)
結(jié)合式(22),則速度環(huán)的開環(huán)傳遞函數(shù)為
(26)
式(26)表明速度環(huán)的控制對象是雙慣性型的,由于起重機(jī)的負(fù)載通常較大,第三個(gè)分式的慣性時(shí)間常數(shù)比第二個(gè)分式的慣性時(shí)間常數(shù)大,為了讓調(diào)節(jié)器零點(diǎn)與控制對象的大時(shí)間常數(shù)極點(diǎn)對消,G2的控制參數(shù)滿足以下條件:
(27)
根據(jù)文獻(xiàn)[13]中最佳整定方法的“模最佳系統(tǒng)”,比例控制參數(shù)可選為
(28)
由以上推導(dǎo),可得到速度環(huán)的閉環(huán)傳遞函數(shù):
(29)
進(jìn)一步推導(dǎo)出從二次單元角位移引出反饋時(shí)的位置外環(huán)的開環(huán)傳遞函數(shù):
(30)
式(30)的頻率特性為
則位置環(huán)簡化的近似條件為
(31)
簡化后的位置外環(huán)的開環(huán)傳遞函數(shù)為
(32)
式(32)是一個(gè)典型的I型系統(tǒng),位置外環(huán)采用P控制:
G1=k1P
(33)
同速度環(huán)的控制器整定方法一樣,控制參數(shù)取
(34)
當(dāng)從起重機(jī)貨物位移引出反饋時(shí),位置外環(huán)的開環(huán)傳遞函數(shù)為
(35)
忽略鋼絲繩阻尼C的影響,當(dāng)滿足以下近似條件:
(36)
則式(35)可簡化成式(32)所示的形式,此時(shí)的位置外環(huán)同樣采用P控制:
(37)
控制參數(shù)取
3.2狀態(tài)觀測器的設(shè)計(jì)

(38)
由于很難得到鋼絲繩的阻尼系數(shù)(通常很小),在狀態(tài)觀測器模型中忽略了鋼絲繩的阻尼力,這樣,觀測器的輸出力包含了鋼絲繩的靜態(tài)力和動(dòng)態(tài)力,寫成
(39)
反饋校正矩陣L可通過零極點(diǎn)配置得到。顯然,負(fù)載位移的估計(jì)值可寫成
(40)
式中,xL0為負(fù)載的初始位置。
4 仿真實(shí)例
某船用起重機(jī)樣機(jī)的額定載荷為9t,最大升沉補(bǔ)償高度為±3m,船舶在波浪作用下的最短升沉運(yùn)動(dòng)周期為9s。機(jī)械傳動(dòng)系統(tǒng)簡圖如圖3所示。

圖3 船用起重機(jī)機(jī)械傳動(dòng)系統(tǒng)簡圖
二次單元通過減速器帶動(dòng)液壓卷筒轉(zhuǎn)動(dòng),控制負(fù)載的垂向位移。
折臂式起重機(jī)主動(dòng)式升沉補(bǔ)償系統(tǒng)組成如圖4所示。圖中1為液壓卷筒,軸測安裝有旋轉(zhuǎn)編碼器,測量卷筒的角位移和角速度;在滑輪2處安裝有銷軸式力傳感器,可測量鋼絲繩張力。二次單元選用力士樂公司的A4VSO355軸向柱塞馬達(dá),配SYHNC100數(shù)字控制器,變量缸位置環(huán)為比例控制,速度環(huán)為PI控制,滿足控制器設(shè)計(jì)的要求。

1.液壓卷筒 2.滑輪 3.負(fù)載圖4 折臂式起重機(jī)主動(dòng)式升沉補(bǔ)償系統(tǒng)組成
整套系統(tǒng)的仿真參數(shù)見表1。表1中,鋼絲繩剛度k為10m長度下的剛度系數(shù)。

表1 升沉補(bǔ)償控制系統(tǒng)仿真參數(shù)表
對于上文構(gòu)造的三環(huán)位置隨動(dòng)系統(tǒng),調(diào)節(jié)器的設(shè)計(jì)方法是從內(nèi)環(huán)到外環(huán)逐個(gè)設(shè)計(jì)。逐環(huán)設(shè)計(jì)可以使每個(gè)控制環(huán)都是穩(wěn)定的,從而保證整個(gè)系統(tǒng)的穩(wěn)定性,當(dāng)變量油缸位置環(huán)和轉(zhuǎn)速環(huán)內(nèi)的對象參數(shù)變化或受到擾動(dòng)時(shí),變量油缸位置反饋和轉(zhuǎn)速反饋能夠起到及時(shí)的抑制作用,使之對負(fù)載位置環(huán)的工作影響最小。同時(shí),每個(gè)環(huán)節(jié)都有自己的控制對象,分工明確,易于調(diào)整。
從頻域角度講,設(shè)計(jì)者希望控制系統(tǒng)具有足夠的頻寬,以快速補(bǔ)償外界擾動(dòng)。由式(3)可計(jì)算得到變量油缸位置內(nèi)環(huán)的開環(huán)截止頻率ωc3=35rad/s,滿足近似條件式(21);同樣可求得速度環(huán)的開環(huán)截止頻率ωc2=15.9rad/s,滿足近似條件式(24);位置外環(huán)的開環(huán)截止頻率ωc1=8.68rad/s,滿足近似條件式(36)。采用完整的系統(tǒng)動(dòng)力學(xué)模型而非簡化模型(式(32)和式(35)為其簡化模型),代入表1所示的參數(shù)并使用MATLAB進(jìn)行仿真,得到系統(tǒng)的開環(huán)傳遞函數(shù)Bode圖如圖5、圖6所示。

1.二次單元角位移對控制輸入的幅頻特性曲線2.貨物位移對控制輸入的幅頻特性曲線圖5 不同反饋連接的系統(tǒng)Bode圖

圖6 完整模型和簡化模型的Bode圖對比
從圖5可以看出,系統(tǒng)穿越頻率大約在8.7rad/s(約1.4Hz)處,可以滿足補(bǔ)償1/9Hz艦船升沉運(yùn)動(dòng)的要求;而在52rad/s頻率附近出現(xiàn)一個(gè)諧振峰值,這是由鋼絲繩卷繞系統(tǒng)影響造成的。為了使系統(tǒng)穩(wěn)定,必須使相位裕量和增益裕量均為正值。圖5中的兩條曲線相位裕量均為正值,只要使增益裕量為正值,系統(tǒng)就可以穩(wěn)定了。曲線1的增益裕量為12dB,而曲線2的增益裕量為8.9dB。這表明曲線2系統(tǒng)的穩(wěn)定性比曲線1系統(tǒng)的穩(wěn)定性要差,這是因?yàn)榍€2系統(tǒng)在曲線1系統(tǒng)的基礎(chǔ)上串聯(lián)了由鋼絲繩卷繞系統(tǒng)構(gòu)成的振蕩環(huán)節(jié),提高了諧振頻率處的峰值,使穩(wěn)定性變差。可以看出,由二次單元角位移反饋構(gòu)成的閉環(huán)系統(tǒng)的穩(wěn)定性比從貨物位移反饋構(gòu)成的閉環(huán)系統(tǒng)的穩(wěn)定性要好。
圖6表明簡化后的系統(tǒng)和完整系統(tǒng)在低頻段的特性是基本一致的,從而證明本文所提模型簡化方法的有效性。需要指出的是,上文提出的逐環(huán)設(shè)計(jì)方法也有不足,即對最外環(huán)控制作用的響應(yīng)不會(huì)太快,這是因?yàn)樵O(shè)計(jì)每個(gè)外環(huán)時(shí),都要將內(nèi)環(huán)等效成其中的一個(gè)環(huán)節(jié),而這種等效環(huán)節(jié)傳遞函數(shù)之所以能夠成立,是以外環(huán)的截止頻率低于內(nèi)環(huán)為前提的(見式(21)、式(24)、式(36))。特別是當(dāng)鋼絲繩卷繞系統(tǒng)組成的彈簧-阻尼-質(zhì)量塊系統(tǒng)的頻寬小于艦船運(yùn)動(dòng)頻率時(shí),系統(tǒng)將不能獲得好的控制效果。

從圖8可以看出,系統(tǒng)升沉補(bǔ)償精度并不令人滿意,主要是因?yàn)橄辔粶笠鸬恼`差,從圖5中也能得出相同的結(jié)論,系統(tǒng)輸出響應(yīng)至少存在90°以上的相位滯后。但圖8也表明系統(tǒng)具有足夠的頻寬,具備補(bǔ)償周期為9s的船舶的升沉運(yùn)動(dòng)的能力。實(shí)際上,對于這種強(qiáng)位置干擾系統(tǒng),僅依靠閉環(huán)控制很難取得理想的控制效果。為取得更好的控制效果,也可參考負(fù)載模擬器的多余力補(bǔ)償措施[14],采用復(fù)合控制器的設(shè)計(jì)方法:首先忽略外部干擾的影響,采用本文給出的控制器設(shè)計(jì)方法以獲得滿意的軌跡跟蹤性能,然后在此基礎(chǔ)上基于結(jié)構(gòu)不變性原理引入干擾(即艦船升沉
圖7 升沉補(bǔ)償系統(tǒng)閉環(huán)控制方塊圖

圖8 起重機(jī)貨物位移響應(yīng)
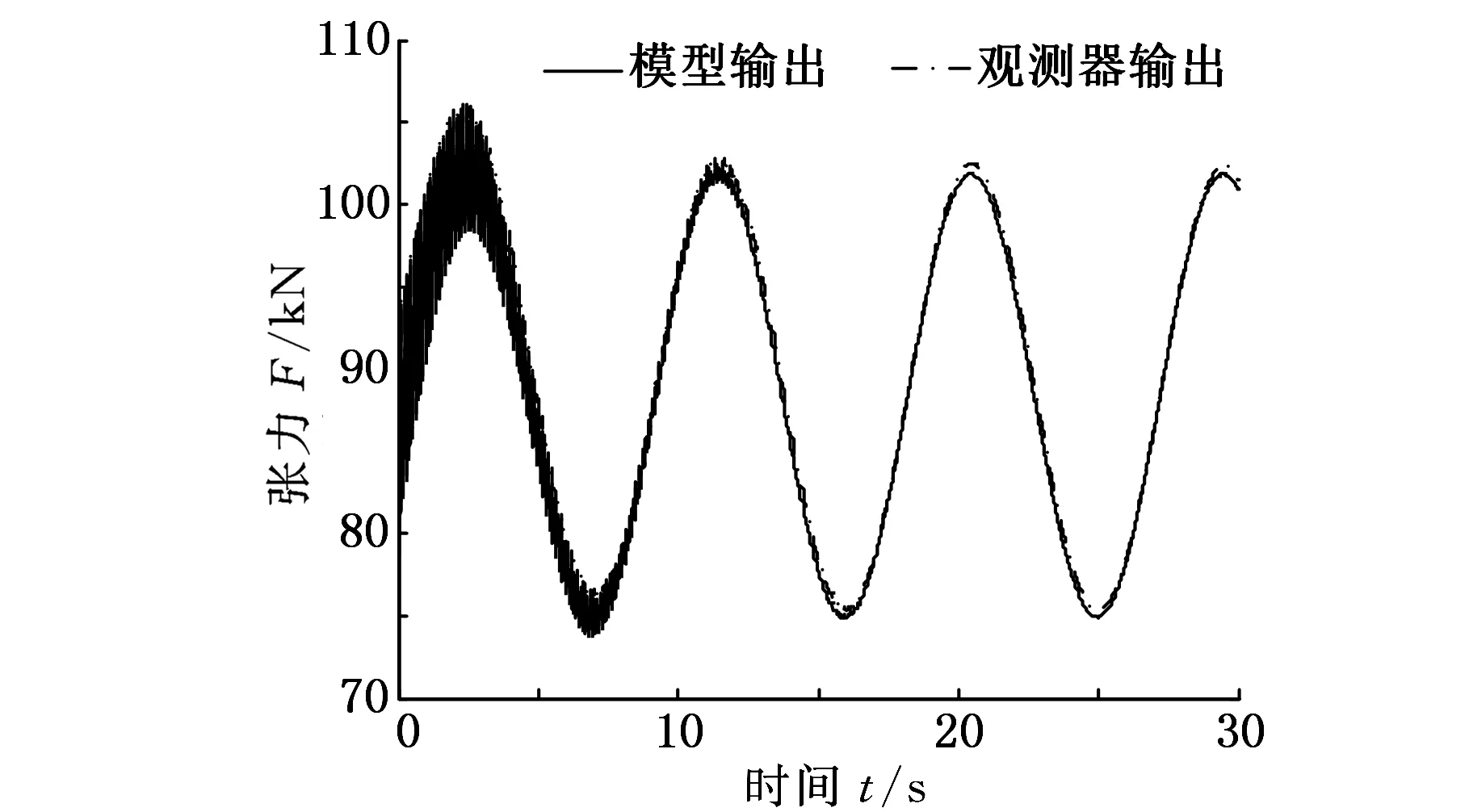
圖9 狀態(tài)觀測器輸出響應(yīng)
運(yùn)動(dòng))的補(bǔ)償措施。圖9表明狀態(tài)觀測器具有較好的收斂速度和觀測精度, 觀測張力誤差控制在900N左右,只占等效拉力的1%,可以滿足系統(tǒng)控制性能要求。
5 結(jié)語
本文基于液壓二次調(diào)節(jié)技術(shù),設(shè)計(jì)了船用起重機(jī)的升沉補(bǔ)償液壓驅(qū)動(dòng)系統(tǒng),建立了系統(tǒng)的完整數(shù)學(xué)模型,構(gòu)造了三環(huán)控制器,并給出了控制器的設(shè)計(jì)方法;基于鋼絲繩的張力檢測,設(shè)計(jì)了狀態(tài)觀測器以得到負(fù)載位移,為工程應(yīng)用打下了基礎(chǔ);最后通過仿真實(shí)例從頻域角度分析了升沉補(bǔ)償系統(tǒng)的動(dòng)態(tài)特性,仿真結(jié)果驗(yàn)證了本文所提控制器設(shè)計(jì)方法、模型簡化方法及模型簡化近似條件的有效性。研究結(jié)果為帶升沉補(bǔ)償功能的起重機(jī)的工程設(shè)計(jì)打下了基礎(chǔ)。
[1]曾智剛. 波浪運(yùn)動(dòng)升沉補(bǔ)償液壓平臺(tái)關(guān)鍵問題試驗(yàn)研究[D].廣州:華南理工大學(xué), 2010.
[2]王海波, 王慶豐. 拖體被動(dòng)升沉補(bǔ)償系統(tǒng)非線性建模及仿真[J].浙江大學(xué)學(xué)報(bào)(工學(xué)版), 2008, 42(9): 1568-1572.WangHaibo,WangQingfeng.Non-linearModelingandSimulationofTowedBodyPassiveHeaveCompensationSystem[J].JournalofZhejiangUniversity(EngineeringScience), 2008, 42(9): 1568-1572.
[3]ZhengH,LiuS,HuQ.SimulationofFuzzyPIDControlofHeaveCompensationSystemforDeep-oceanMining[J].WorldJournalofModellingandSimulation, 2012, 8(1): 50-57.
[4]吳百海, 肖體兵, 龍建軍,等. 深海采礦裝置的自動(dòng)升沉補(bǔ)償系統(tǒng)的模擬研究[J].機(jī)械工程學(xué)報(bào), 2003, 39(7): 128-133.
WuBaihai,XiaoTibin,LongJianjun,etal.SimulationStudyonAutomaticHeaveCompensationSystemforDeep-oceanMiningEquipment[J].ChineseJournalofMechanicalEngineering, 2003, 39(7): 128-133.
[5]張大兵, 烏建中, 鄭福來,等. 船用起重機(jī)升沉補(bǔ)償系統(tǒng)建模與仿真[J].中國機(jī)械工程, 2012, 23(7): 794-797.
ZhangDabing,WuJianzhong,ZhengFulai,etal.ModelingandSimulationonHeaveCompensationSystemofShip-mountedCrane[J].ChinaMechanicalEngineering, 2012, 23(7): 794-797.
[6]RexrothBoschGroup.SecondaryControlwithA4VSO/GAxialPistonUnits[EB/OL].http://www.boschrexroth.com/en/xc/products/product-groups/industrial-hydraulics/secondary-control/documentation-and-tools/documentation-and-downloads-9.
[7]戰(zhàn)興群. 靜液驅(qū)動(dòng)二次調(diào)節(jié)技術(shù)控制特性的研究[D].哈爾濱:哈爾濱工業(yè)大學(xué), 2003.
[8]王春行. 液壓控制系統(tǒng)[M].北京:機(jī)械工業(yè)出版社, 2010.
[9]馬登成, 楊士敏, 胡永彪. 靜液二次調(diào)節(jié)加載系統(tǒng)動(dòng)態(tài)性能分析[J].計(jì)算機(jī)仿真,2010, 27(4): 300-303.
MaDengcheng,YangShimin,HuYongbiao.StudyonDynamicCharacteristicsofaSecondaryRegulatedLoadingSystem[J].ComputerSimulation, 2010, 27(4): 300-303.
[10]NestegardA,BoeT.ModelingandAnalysisofMarineOperations[S].DetNorskeVeritas,Norway,RecommendedPracticeDNV-RP-H103, 2011.
[11]KüchlerS,MahlT,NeupertJ,etal.ActiveControlforanOffshoreCraneUsingPredictionoftheVessel’sMotion[J].IEEE/ASMETrans.onMechatronics, 2011, 16(2): 297-309.
[12]滕福林, 胡育文, 劉洋,等.位置/電流兩環(huán)結(jié)構(gòu)位置伺服系統(tǒng)的跟隨性能[J].電工技術(shù)學(xué)報(bào), 2009, 24(10): 40-46.
TengFulin,HuYuwen,LiuYang,etal.TrackingPerformanceofPositionServoSystemOnlywithPositionandCurrentLoops[J].TransactionsofChinaElectrotechnicalSociety, 2009, 24(10): 40-46.
[13]陳伯時(shí). 電力拖動(dòng)自動(dòng)控制系統(tǒng)-運(yùn)動(dòng)控制系統(tǒng)[M].北京:機(jī)械工業(yè)出版社,2004.
[14]焦宗夏,華清,王曉東,等. 電液負(fù)載模擬器的復(fù)合控制[J].機(jī)械工程學(xué)報(bào),2002, 38(12): 34-38.
JiaoZongxia,HuaQing,WangXiaodong,etal.HybridControlontheElectrohydraulicLoadSimulator[J].ChineseJournalofMechanicalEngineering, 2002, 38(12): 34-38.
(編輯陳勇)
Design and Analysis of Active Heave Compensation System for Offshore Cranes
Wu JinboSong Yuchen
Huazhong University of Science and Technology, Wuhan,430074
To compensate the heave motion of the ship’s crane during marine operation, the crane’s hydraulic driving system was constructed based on the secondary regulated hydrostatic drive technology. Firstly, a full mathematic model of the heave compensation system was presented. A triple closed-loop control structure was proposed, which included the position closed-loop of the stroke cylinder fixed in the secondary unit, the speed closed-loop of the secondary regulated hydraulic motor and the position closed-loop of the secondary regulated hydraulic motor. Afterwards, a simple design method was proposed to ascertain the three controllers’ parameters. In order to obtain the position of the crane’s cargo, an observer was designed to estimate this state by using the wire rope tension. Lastly, a design example for the active heave compensation was provided. The dynamic characteristics of the heave compensation system were analyzed from the frequency domain standpoint by numerical simulations, which helpes lay a foundation for control strategy research.
active heave compensation;secondary control unit;marine operation;dynamic characteristics; offshore technology
2015-04-07
國家自然科學(xué)基金資助項(xiàng)目(50909046)
TP391
10.3969/j.issn.1004-132X.2016.15.001
吳金波,男,1974年生。華中科技大學(xué)船舶與海洋工程學(xué)院副教授。主要研究方向?yàn)椴⒙?lián)機(jī)器人、艦船機(jī)電設(shè)備的動(dòng)態(tài)特性分析等。宋宇宸,男,1992年生。華中科技大學(xué)船舶與海洋工程學(xué)院碩士研究生。

