一種聚類優化融合故障診斷方法及其應用

蔣玲莉　莫志軍　陳安華　李學軍

1.湖南科技大學機械設備健康維護湖南省重點實驗室，湘潭，4112012.蘇州東陵振動試驗儀器有限公司，蘇州，215163

?

一種聚類優化融合故障診斷方法及其應用

蔣玲莉1,2莫志軍1陳安華1李學軍1

1.湖南科技大學機械設備健康維護湖南省重點實驗室，湘潭，4112012.蘇州東陵振動試驗儀器有限公司，蘇州，215163

針對單一聚類診斷方法難以準確、全面識別不同故障狀態的問題，提出了一種聚類優化融合故障診斷方法。分別利用社團聚類、K-均值聚類及粒子群聚類三種方法對故障進行識別，得出三種聚類方法對應的故障識別準確率，在此基礎上構建初始權值矩陣，并通過遺傳算法對初始判斷矩陣與三種聚類方法進行優化，得到最優權值矩陣與優化的聚類模型，用于融合診斷。軸承故障診斷實例結果表明，該聚類融合診斷方法能夠有效提高故障識別準確率。

聚類分析；權值矩陣；融合診斷；遺傳算法

0　引言

聚類分析方法被用作描述數據、衡量不同數據源間的相似性、將數據源劃分為各類集合[1-2]，被廣泛應用于故障模式識別[3-4]。大部分故障聚類診斷方法通過描述故障特征間聯系緊密程度的聚類變量來實現故障模式識別，聚類變量主要存在兩種方式：一是采用描述故障特征之間的接近程度的指標，例如“距離”，“距離”越小的變量越具有相似性，傳統的故障診斷聚類方法如K-均值聚類[6]、粒子群聚類[7]、灰色聚類[8]等的測量方式就歸于此類；二是采用表示故障特征之間相似程度的指標，例如“相關系數”，“相關系數”越大的故障特征越具有相似性，社團聚類中的模塊度就是典型的“相關系數”[5]，不僅可以表示單個樣本特征模塊之間的相似性，而且能夠描繪出大規模模塊之間的相似程度。各種聚類診斷方法各有優劣，實際應用中各有適用性，如K-均值聚類需知故障類別等先驗知識，粒子群聚類容易陷入局部最優，社團聚類雖無需故障類別數等先驗知識，卻容易多分類或少分類而導致誤判?？偠灾?，單一聚類診斷方法通用性差，不具備全面的、良好的識別所有故障狀態的能力。對聚類方法進行融合可提高故障診斷適用性，保證診斷精度?；诖耍疚奶岢隽艘环N聚類優化融合故障診斷方法，分別利用社團聚類、K-均值聚類及粒子群聚類三種方法進行故障識別，在此基礎上構建初始權值矩陣，并通過遺傳算法對初始判斷矩陣及三種聚類方法進行優化，得到最優權值矩陣與優化的聚類模型，進行融合診斷。最后以軸承故障診斷實例驗證了融合診斷的優越性。

1　聚類優化融合故障診斷方法

1.1聚類優化融合診斷模型

融合診斷方法主要分為串行診斷融合與并行診斷融合，由于單一診斷方法的排列順序對串行融合診斷的診斷結果影響過大，因而在本文中選取并行診斷融合。聚類優化融合的流程框圖見圖1。

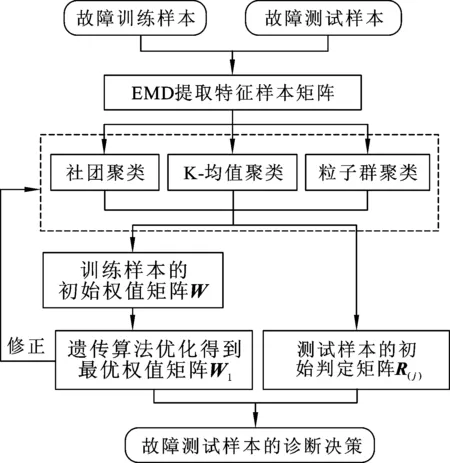
圖1　融合聚類診斷流程圖

聚類優化融合的步驟如下：

(1)故障信號集包含m類故障，共計b個故障樣本，m類故障分別用G=(G1,G2,…,Gm)來表示，提取故障信號的N維特征向量，構成b×N特征樣本矩陣Q，矩陣Q的每一行是一個故障樣本特征向量。本文以經驗模態分解(EMD)所得各階能量值為特征向量[9]。

(2)采用選定的K種方法分別對矩陣Q進行聚類診斷，得到K種方法的診斷結果，矢量Pk=(P1k,P2k, …,Pmk)T表示第k(k=1,2,…,K)類方法對第m類故障的識別正確率，矢量R=(Rk1,Rk2,…,Rkm)表示第k類方法對樣本Q(j)的判定結果(j=1,2,…,b)，Rki為第k種診斷方法對應Gi類故障的診斷結果(i=1,2, …,m)，且有

本文分別用社團聚類、K-均值聚類及粒子群聚類三種方法進行聚類診斷。

(3)對矢量P進行預加權調整，得到初始權值矩陣W：

(1)

(2)

其中，Wik表示第k種方法對Gi類故障判定時所占權值。

(4)由矢量R得到K種聚類診斷方法對所有單個故障樣本Q(j)的初始判定矩陣R(j):

(3)

(5)用遺傳算法優化融合權值矩陣，迭代結束后根據適應度函數得到優化后的權值矩陣W1；遺傳算法在優化權值矩陣的同時，對三種聚類方法的錯誤診斷予以修正，優化聚類模型。

(6)故障樣本Q(j)的最終診斷結果為Val(j)，則有

Vj=(V1,V2,…,Vm)=diag(W1R(j))

(4)

Vjmax=max(V1,V2,…,Vm)

(5)

當Vi=Vjmax時，取Val(j)=i,即判定故障樣本Q(j)屬于Gi類故障。

1.2基于遺傳算法的融合權值矩陣優化

從融合診斷模型中可以看出，權值矩陣W在很大程度上決定了最終診斷正確率，在本文中，采用遺傳算法[10]對權值矩陣W進行優化。

本文中遺傳算法的應用步驟如下：

(1)將初始權值矩陣W的權值因子作為初始種群個體進行編碼。隨機產生初始種群，個體數目一定，每個個體表示染色體的基因編碼，由于二進制編碼方法的編碼、解碼操作簡單易行，且便于實現交叉、變異等遺傳操作，因而在本文中選用二進制編碼方法對融合權值矩陣進行編碼，并設定好求解精度。圖2所示為本文中權值矩陣串聯編碼組合而成的染色體。

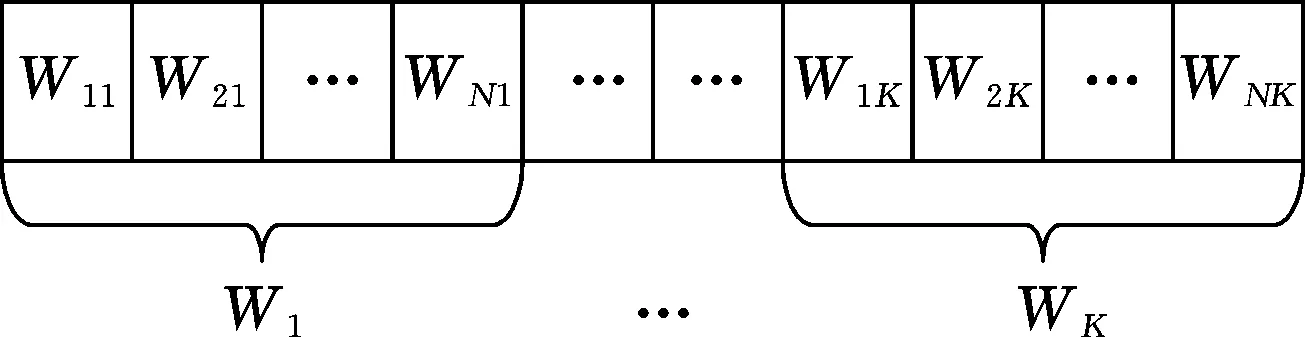
圖2　融合權值矩陣串聯編碼組合后的染色體

(2)對個體適應度函數值進行計算。適應度函數在遺傳算法中不僅表明了函數解的優劣，而且決定了個體的進化方向，當適應度函數增大到收斂時，訓練樣本的診斷正確率相應收斂到最大值。本文定義適應度函數Fit(Wc)[11]如下：

(6)

(7)

(8)

其中，Wc為每一次迭代過程中的權值矩陣輸入值，當訓練樣本故障聚類診斷正確時，函數G(Wc)取值為1；反之，函數G(Wc)在0～1范圍內取值，b1為訓練樣本總數。

每一次迭代過程中，首先計算出所有個體的適應度函數值，具體計算過程是以個體染色體解碼后得到的權值矩陣Wc作為輸入，按照式(4)、式(5)對所有訓練樣本依次進行診斷判定，再代入式(6)、式(7)求得個體的適應度函數值，其值越大，復制到下一代的概率越高，根據遺傳算法的輪盤選擇機制獲取最優遺傳個體，并判斷最優個體是否符合優化準則，若符合，輸出自家個體代表的最優解，并結束計算，否則繼續進行步驟(3)。

(3)對權值矩陣進行優化。權值矩陣的優化具體體現為種群個體適應度函數值的提高，依據種群中個體適應度函數選擇復制個體，適應度高的個體選擇復制的概率高，適應度低的個體則可能被淘汰；對當次循環中最優個體返回的染色體進行解碼，即可得到當次循環優化后的權值矩陣。

(4)交叉生成新個體。對于步驟(3)中適應度值低的個體，按照一定的交叉概率與交叉方法生成新的個體并添加到種群中，進行下一輪迭代；其中交叉方法選定為單點交叉，如圖3所示。

圖3單點交叉

圖3單點交叉(5)變異生成新個體。對于步驟(3)中適應度值低的個體，按照一定的變異概率與變異方法，生成新的個體添加到種群中，在種群個體數保持不變的情況下進行下一輪迭代，變異方法如圖4所示。

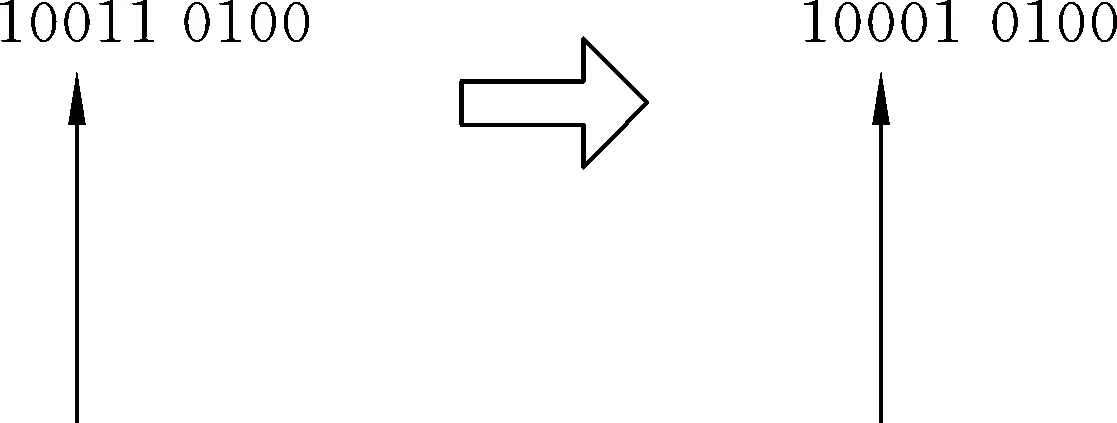
圖4　變異

(6)迭代求取最優權值矩陣。由交叉和變異產生新一代的種群，返回步驟(2)，進行下一輪迭代；通過交叉操作和變異操作，調整適應度值低的個體權值矩陣編碼，當訓練樣本故障分類判定錯誤時，在下一輪迭代中，正確判定故障分類的方法權值得到提高，并相應調低錯誤判定故障分類的方法權值，實現新生個體適應度函數值的增加；當達到設定的迭代最大次數時，迭代完成，此時若適應度函數并未收斂，則需增大迭代次數，直到滿足優化準則中的一條，結束計算，并返回最優權值矩陣。

其中步驟(2)與步驟(6)的優化準則如下(設定滿足其中一條即可)：①種群中個體的平均適應度超過預先設定值，預先設定值由適應度值可能達到的最大值與求解精度決定；②適應度函數在達到種群世代數前收斂(運行到超過預先設定值，即迭代次數達到/超過最大值)。

權值矩陣優化流程圖如圖5所示。

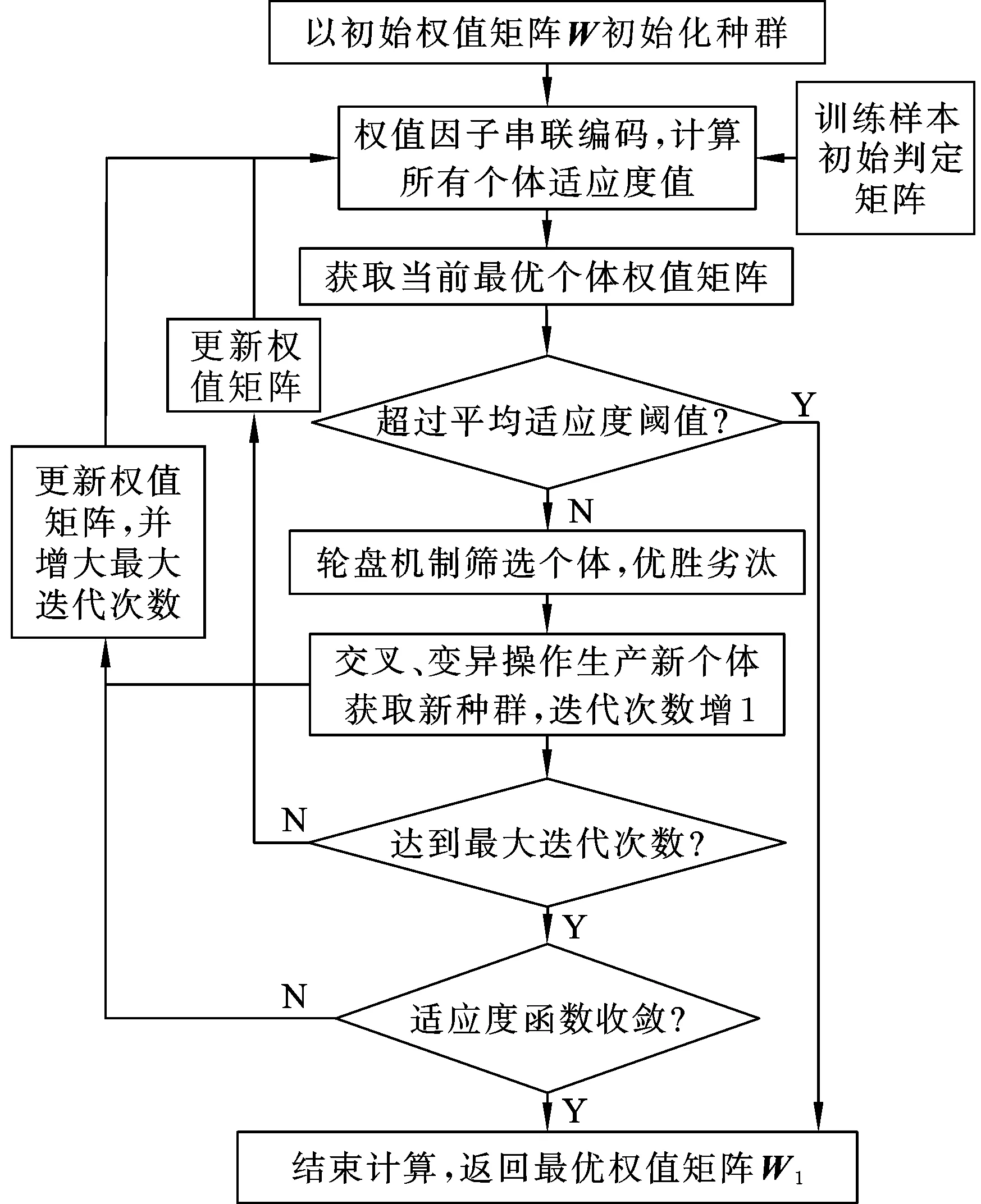
圖5　權值矩陣優化流程圖

2　應用實例

通過機械故障綜合模擬實驗臺分別采集內圈故障、滾珠故障、正常狀態和外圈故障4種單一模式下的軸承振動信號，每種故障狀態分別對應一個模擬故障軸承，各軸承結構尺寸一致，分別進行振動測試，實驗臺工作轉頻為1797 r/min，采樣頻率為12 kHz。

隨機選取軸承內圈故障、滾珠故障、正常狀態和外圈故障樣本各100個，共400個訓練樣本，用EMD方法提取每類狀態的樣本特征，取每組特征向量的前7維構成訓練樣本矩陣Q。分別采用社團聚類算法、K-均值聚類算法與粒子群聚類算法對軸承故障訓練樣本進行聚類診斷，每類算法取10次聚類診斷的平均結果作為最終診斷輸出，結果見表1。則有

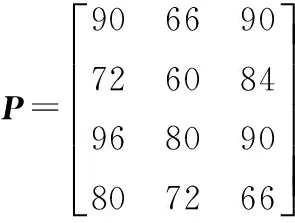
表1三種聚類方法對訓練樣本單一診斷正確率 %

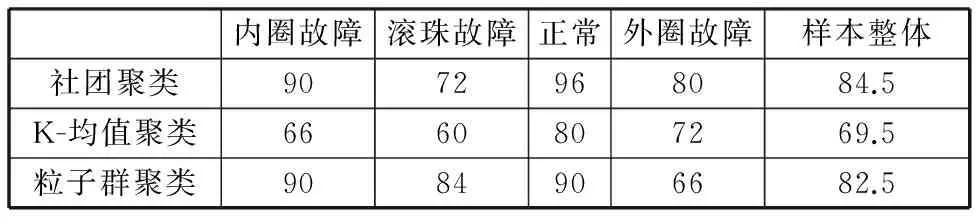
內圈故障滾珠故障正常外圈故障樣本整體社團聚類9072968084.5K-均值聚類6660807269.5粒子群聚類9084906682.5

對P進行預加權調整，根據式(2)有

同理，可計算得到初始權值矩陣W：

采用遺傳算法優化初始權值矩陣，過程原理如下。

假設某一訓練樣本j為軸承滾珠故障樣本，用社團聚類、K-均值聚類和粒子群聚類3種診斷方法分別判定其為軸承內圈故障、軸承滾珠故障和正常狀態，由式(3)得該訓練樣本的初始判斷矩陣R(j)：

其中，初始判斷矩陣R(j)的4列分別對應4種軸承狀態：內圈故障、滾珠故障、正常狀態和外圈故障，3行分別對應3種診斷方法：社團聚類、K-均值聚類和粒子群聚類。

由式(8)可得

Vjmax=0.3659，最大值處于第1列，即融合診斷后判定訓練樣本j為內圈故障，判定錯誤，通過交叉操作和變異操作對初始權值矩陣W進行調整，使W11變小，W22變大，同時修正聚類模型。再對訓練樣本j進行判定，得

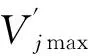
本文將初始權值矩陣W按照圖3的順序編碼成二進制數值串，遺傳算法具體參數參照文獻[11]設定，見表2。

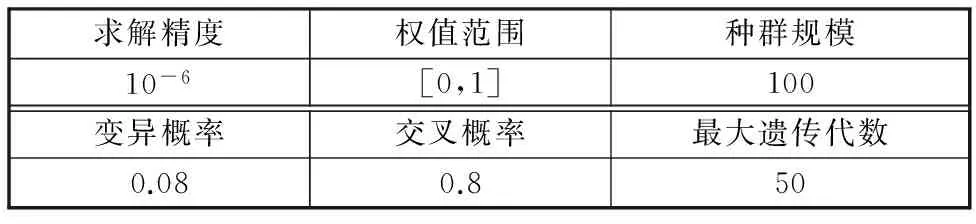
表2　遺傳算法參數設置

圖6所示為適應度函數值隨著遺傳代數的變化曲線，設定個體平均適應度閾值為1×10-6，可以發現在進行第11次迭代時適應度函數已經收斂，滿足優化準則2，結束運算，得到優化后的權值矩陣W1：

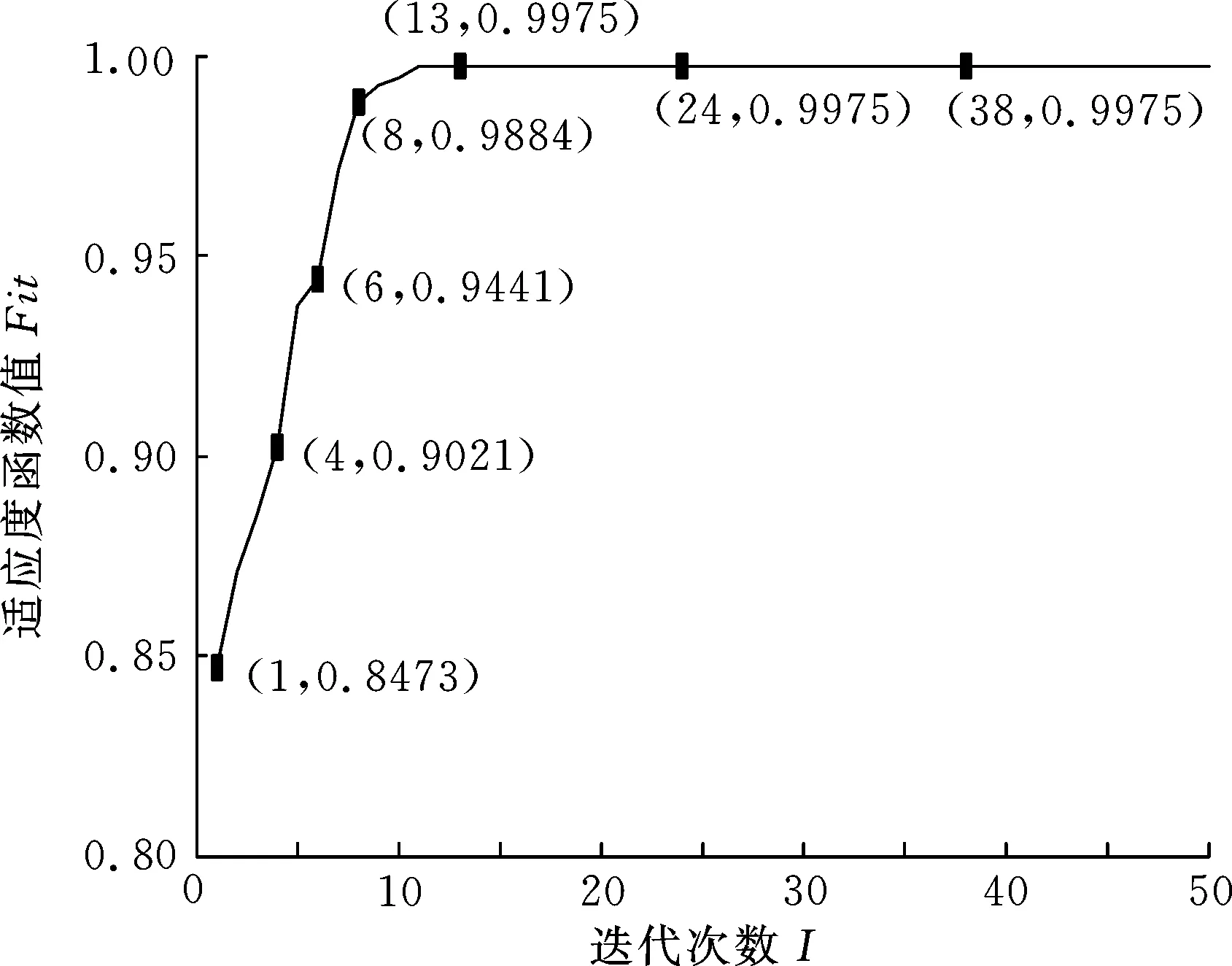
圖6　遺傳算法適應度函數值隨迭代次數變化

得到最優權值矩陣W1并對聚類模型進行優化后，便可對樣本進行聚類融合診斷。

隨機選取軸承內圈故障、滾珠故障、正常狀態和外圈故障樣本各100個，對400個測試樣本進行聚類融合診斷，診斷結果見表3。

表3　聚類優化融合對測試樣本診斷正確率　%

對比表3與表1可知，聚類優化融合診斷整體識別率明顯提高，滾動體故障與正常狀態能夠完全識別，內圈故障識別率提高到96%，外圈故障識別率提高到88%。這說明聚類優化融合診斷方法明顯優于單一聚類診斷方法。

3　結語

本文提出了一種聚類優化融合故障診斷方法，通過單一聚類診斷獲得初始權值矩陣，利用遺傳算法優化判定權值與聚類模型，聚類融合診斷取長補短，消除了單一融合診斷方法的不確定性與片面性，以軸承故障診斷實例驗證了該方法的優越性，本文研究結果有重要的應用參考價值。

[1]Deng Zhaohong,Choi K S,Chung Fulai,et al.Enhanced Soft Subspace Clustering Integrating within Cluster and Between-cluster Information[J].Pattern Recognition, 2010,43(3):767-781.

[2]Everitt B S,Landau S,Leese M,et al.Cluster Ana-lysis [M]. London: Wiley,2011.

[3]Park H S,Jun C H.A Simple and Fast Algorithm for K-medoids Clustering[J].Expert Systems with Applications,2009,36(2):3336-3341.

[4]陳安華,周博,張會福，等.基于改進人工魚群算法的機械故障聚類診斷方法[J].振動與沖擊,2012,31(17):145-148.

Chen Anhua，Zhou Bo，Zhang Huifu，et al.A Clustering Method for Mechanical Fault Diagnosis Based on Improved Fish-swarm Algorithm[J].Journal of Vibration and Shock,2012,31(17):145-148.

[5]陳安華,潘陽,蔣玲莉.基于復雜網絡社團聚類的故障模式識別方法研究[J].振動與沖擊,2013,32(20):129-133.

Chen Anhua,Pan Yang,Jiang Lingli.Fault Pattern Recognition Method Based on Complex Community Clustering[J].Journal of Vibration and Shock,2013,32(20)：129-133.

[6]Richhariya V,Sharma N.Optimized Intrusion Detection by CACC Discretization via Naive Bayes and K-Means Clustering[J].International Journal of Computer Science & Network Security，2014，14(1)：54-58.

[7]Runkler T A, Katz C.Fuzzy Clustering by Particle Swarm Optimization[C]//IEEE International Conference on Fuzzy Systems.Vancouver,2006: 601-608.

[8]Liu Y C,Xu J X.Risk Evaluation of CCIT Model in Ant Colony Housing Supply Based on AHP-grey Clustering Method[J].Applied Mechanics and Materials,2013, 380/384: 2520-2523.

[9]蔡艷平，李艾華，石林鎖，等.基于EMD與譜帩度的滾動軸承故障檢測改進包絡譜分析[J].振動與沖擊，2011，30(2)：167-172.

Cai Yanping，Li Aihua，Shi Linsuo，et al.Roller Bearing Fault Detection Using Improved Envelope Spectrum Analysis Based on EMD and Spectrum Kurtosis[J]. Journal of Vibration and Shock，2011，30(2)：167-172.

[10]Holland J H.Adaptation in Natural and Artificial Systems：an Introductory Analysis with Applica-tions to Biology，Control，and Artificial Intelligence[M].2nd ed.Cambridge：MIT Press，1992.

[11]何大闊,王福利,張春梅.基于均勻設計的遺傳算法參數設定[J].東北大學學報(自然科學版),2003,24(5):409-411.

He Dakuo,Wang Fuli, Zhang Chunmei.Establishment of Parameters of Genetic Algorithm Based on Uniform Design[J].Journal of Northeastern University(Natural Science),2003,24(5):409-411.

(編輯陳勇)

Clustering Optimization Fusion Method for Fault Diagnosis and Its Applications

Jiang Lingli1,2Mo Zhijun1Chen Anhua1Li Xuejun1

1.Hunan Provincial Key Laboratory of Health Maintenance for Mechanical Equipment,Hunan University of Science and Technology, Xiangtan, Hunan, 411201 2. Suzhou Dongling Vibration Test Instrument Limited Company, Suzhou, Jiangsu, 215163

Single community diagnosis clustering methods were difficult to identify different fault states, in order to improve diagnostic accuracy, a fusion clustering method was proposed herein based on genetic optimization algorithm. Three clustering methods, the community clustering, the K-means clustering and the particle swarm clustering, were used to identify the fault states respectively. The diagnostic accuracies were used to construct an initial weight matrix. The genetic optimization algorithm was used to optimize the weight matrix. The examples of bearing fault diagnosis show that the clustering optimization fusion method may improve diagnostic accuracy.

clustering analysis;weight matrix;fusion diagnosis;genetic algorithm

2015-10-09

國家自然科學基金資助項目(51575177)；湖南省教育廳優秀青年項目(14B057) ；湖南省教育廳資助重點項目(13A023)

TP206.3 ；TH17DOI：10.3969/j.issn.1004-132X.2016.15.012

蔣玲莉，女，1981年生。湖南科技大學機械設備健康維護省重點實驗室副教授，蘇州東陵振動試驗儀器有限公司博士后研究人員。主要研究方向為動力學與故障診斷。莫志軍，男，1992年生。湖南科技大學機電工程學院碩士研究生。陳安華，男，1963年生。湖南科技大學機械設備健康維護省重點實驗室教授。李學軍，男，1969年生。湖南科技大學機械設備健康維護省重點實驗室教授。