基于擴展卡爾曼濾波的人體行為識別算法

任子良，秦 勇，黎志雄

（東莞理工學院 計算機學院，廣東 東莞　523808）

基于擴展卡爾曼濾波的人體行為識別算法

任子良，秦 勇，黎志雄

（東莞理工學院 計算機學院，廣東 東莞523808）

針對人體行為事件，研究了多傳感器數(shù)據(jù)采集模型和擴展卡爾曼濾波優(yōu)化算法的應用。系統(tǒng)將加速度傳感器分量數(shù)據(jù)映射為三維加速度空間，并與壓力傳感器數(shù)據(jù)結合建立四維實時數(shù)據(jù)采集空間。基于系統(tǒng)的模型特征，提出了非線性系統(tǒng)下的擴展卡爾曼濾波算法。系統(tǒng)利用優(yōu)化算法對數(shù)據(jù)實現(xiàn)最優(yōu)估計，并依據(jù)傳感器信噪比對優(yōu)化數(shù)據(jù)進一步修正，之后在系統(tǒng)設定的傳感器信任級別和融合權重的基礎上完成人體行為識別。實驗結果表明，本文算法可以提高數(shù)據(jù)空間的精度和平滑度，可對人體行為進行有效識別。

傳感器數(shù)據(jù)；人體行為；擴展卡爾曼濾波；優(yōu)化算法；加權融合

最優(yōu)狀態(tài)估計方法被廣泛應用于參數(shù)估計、系統(tǒng)控制、數(shù)據(jù)融合等領域。卡爾曼濾波（Kalman Filter）作為最優(yōu)狀態(tài)估計的常用無偏估計方法，可以有效處理線性系統(tǒng)問題。對于弱非線性系統(tǒng)問題，可將系統(tǒng)線性化后再進行卡爾曼優(yōu)化處理。

日常生活中，人體活動的行為可描述為靜止、走路、跑步、跳躍和跌倒等。針對人體行為的識別，常用方法有基于人體點模型匹配方法和基于狀態(tài)空間的識別方法等。而所有方法均需要對系統(tǒng)參數(shù)或采集的數(shù)據(jù)進行優(yōu)化估計處理，以降低系統(tǒng)噪聲干擾和提高系統(tǒng)估計精度，達到提高系統(tǒng)整體可靠性的目的。

本文建立了弱非線性系統(tǒng)模型，提出了擴展卡爾曼濾波和信任級別權重融合相結合的算法來對人體行為進行識別。所采用的擴展卡爾曼濾波算法（Extended Kalman Filter）對數(shù)據(jù)空間進行二階優(yōu)化估計可達到二階精度。算法先將系統(tǒng)模型的觀測方程做線性化處理，應用擴展卡爾曼濾波優(yōu)化算法處理實時數(shù)據(jù)，并以數(shù)據(jù)協(xié)方差來修正，進一步在傳感器信任級別的基礎上進行權重融合和人體行為識別。

1　系統(tǒng)模型

本文系統(tǒng)采用三軸加速度傳感器和壓力傳感器采集人體行為數(shù)據(jù)，可映射為一非線性二階離散系統(tǒng)。

依據(jù)加速度基本物理原理，將人體行為中的矢量加速度以g=9.8 m/s2為單位映射到三維加速度空間，其三維方向上分量分別為Gx、Gy和Gz如圖1所示。壓力傳感器采集人體壓力數(shù)據(jù)F，與加速度矢量一并構成系統(tǒng)模型所需的四維狀態(tài)數(shù)據(jù)空間（Gx，Gy，Gz，F(xiàn)）T。

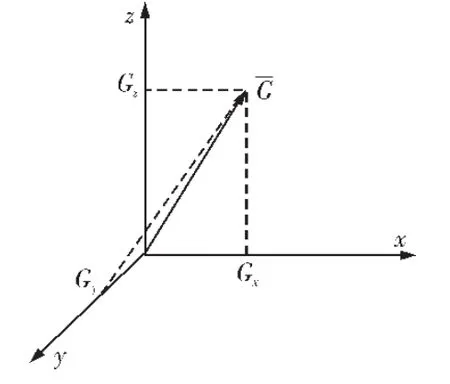
圖1　三維加速度空間映射圖Fig.1　Three-dimensional acceleration space mapping

系統(tǒng)建模為如下二階非線性離散系統(tǒng)，包括過程方程和非線性觀測方程：

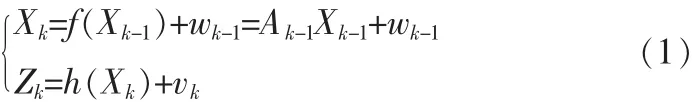
其中，Xk=（Gx，Gy，Gz，F(xiàn)）T為系統(tǒng)采集的離散數(shù)據(jù)向量，wk為數(shù)據(jù)向量所對應的過程噪聲，vk為對應的系統(tǒng)測量噪聲，Ak為單位系數(shù)矩陣，h（Xk）為系統(tǒng)的二階、多參數(shù)非線性映射。通過求h（Xk）的雅克比矩陣得出系統(tǒng)的線性化系數(shù)矩陣Hk。

根據(jù)EKF算法，得到系統(tǒng)模型的過程方程和線性化觀測方程為：

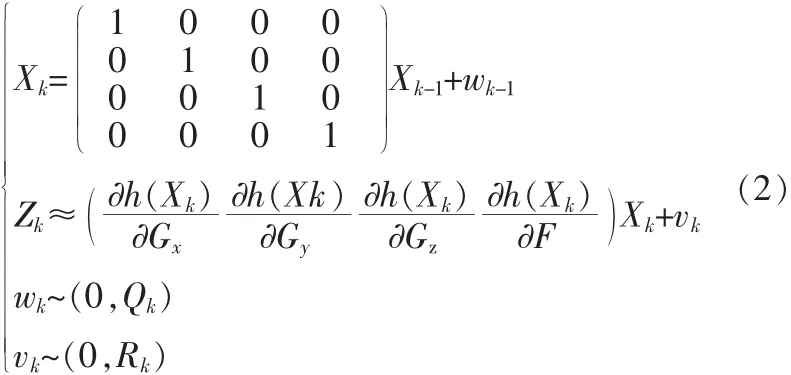
其中k為數(shù)據(jù)離散采集時間步長，wk～（0，Qk）和vk～（0，Rk）表示過程噪聲和觀測噪聲，協(xié)方差矩陣分別為Qk和Rk。

2　算法建模

根據(jù)系統(tǒng)模型對四維矢量數(shù)據(jù)采集和處理的需要，本文設計算法流程如圖2所示。

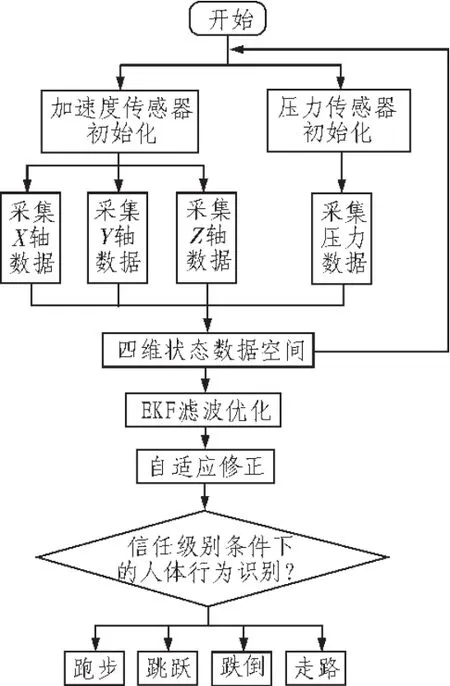
圖2　人體行為識別流程圖Fig．2　Flow chart of human action recognition

算法處理步驟如下：

1）系統(tǒng)依據(jù)傳感器特性分別對采集數(shù)據(jù)的加速度傳感器和壓力傳感器進行數(shù)據(jù)空間的初始化。

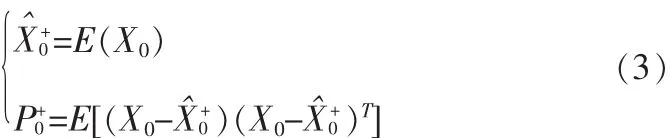
2）加速度傳感器和壓力傳感器分別循環(huán)采集離散數(shù)據(jù)，構成四維矢量數(shù)據(jù)并輸出。系統(tǒng)根據(jù)采集的四維矢量數(shù)據(jù)和采樣頻率，分別設置迭代次數(shù)為600次和迭代步長為0．02 s。

傳統(tǒng)青花本身就是當時社會文化的具體反應，它對現(xiàn)實的寫照，是客觀存在的。因此每一件青花瓷器物的產(chǎn)生，它的背景都蘊含著深厚的歷史文化及審美。作為人類的精神產(chǎn)物，它上面的總總反應，如題材，繪制技法都是不可磨滅的。因此，我們在用現(xiàn)代青花進行創(chuàng)作時候絕不能一味否定過去，而是應該帶著歷史發(fā)展的眼光對待。

3）擴展卡爾曼優(yōu)化算法處理數(shù)據(jù)空間矢量值，得到優(yōu)化估計值。分別對系統(tǒng)進行時間更新和量測更新。

①時間更新

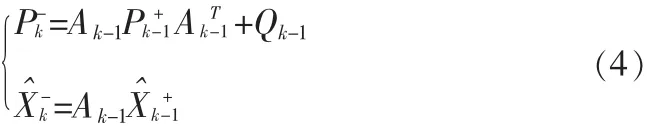
②線性化測量方程系數(shù)矩陣，得到測量更新的近似線性系數(shù)矩陣Hk。

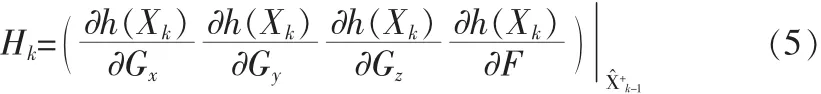
③量測更新

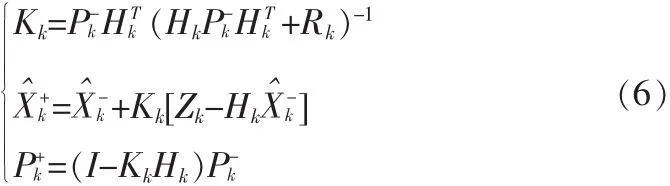
其中，Kk和Rk分別表示卡爾曼增益矩陣和量測噪聲矩陣，其噪聲與Qk同樣由傳感器信噪比SNR=40 dB給出。系統(tǒng)所采集的離散矢量數(shù)據(jù)不斷迭代優(yōu)化，以得到量測更新值即收斂于實際值的優(yōu)化估計值。

4）依據(jù)傳感數(shù)據(jù)的信噪比和噪聲協(xié)方差矩陣對數(shù)據(jù)進行加權修正。

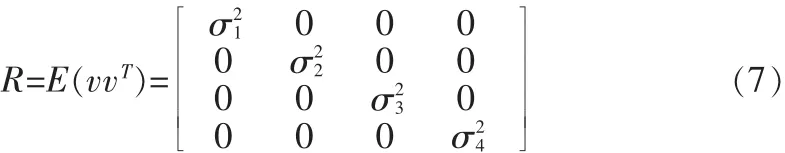
則對EKF迭代優(yōu)化值修正為：

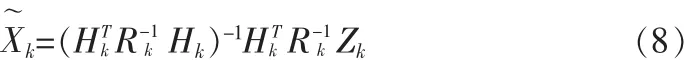
5）依據(jù)各傳感器信任級別和融合權重進行人體行為識別。

根據(jù)人體行為識別的有效性和對采集數(shù)據(jù)矢量分量的依賴程度，設置數(shù)據(jù)空間各分量的信任級別為A、B、C、D，對應的權重分別為P（A）、P（B）、P（C）、P（D），且P（A）+P（B）+P（C）+P（D）=1，得到系統(tǒng)識別人體行為的最終判別數(shù)據(jù)為：

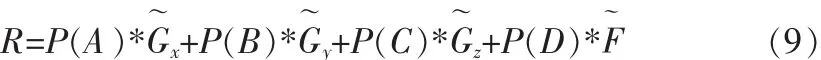
3　系統(tǒng)實驗與分析

系統(tǒng)模型以k=0．02 s為時間步長，離散采集走路、跑步、跳躍和跌倒等人體行為數(shù)據(jù)。在對采集到的數(shù)據(jù)EKF仿真過程中，分別對每種行為數(shù)據(jù)截取150組數(shù)據(jù)來迭代優(yōu)化和修正，數(shù)據(jù)對比如圖3所示。

從圖3可知，人體行為中走路的X軸、Y軸和Z軸加速度分量值取值區(qū)間為［0，0．8］、［-0．3，0．38］和［0．1，0．8］，跑步分量取值區(qū)間為［-0．5，0．5］、［-0．2，0．7］和［-0．1，1．3］，跳躍分量取區(qū)間為［-0．5，0．7］、［-0．1，0．5］和［0，1．7］，跌倒分量取值區(qū)間為［-0．1，1．7］、［-0．2，1］和［-0．1，1．3］。因為壓力數(shù)據(jù)只有當?shù)箷r才為零，因此截取跑步行為數(shù)據(jù)如圖3（d）所示。

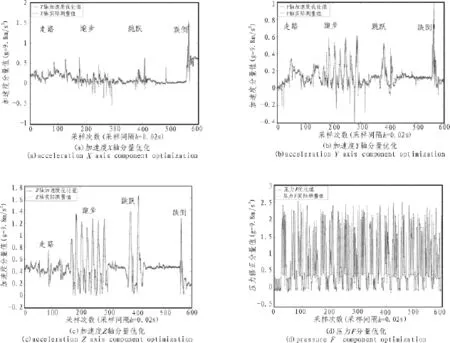
圖3　人體行為加速度仿真圖Fig．3　Acceleration of human action simulation

通過對比各種人體行為的取值范圍和頻率可知，跑步和跳躍的取值大小近似，跳躍有兩次數(shù)據(jù)顯著變化，跌倒數(shù)據(jù)有一次顯著變化且跌倒后壓力數(shù)據(jù)為零。系統(tǒng)通過式（9）計算R值，并依據(jù)給定的閾值范圍進行人體行為識別。

表1為本文走路、跑步、跳躍與跌倒各實驗50次的人體行為識別情況：

表1　實驗結果Tab.1 Test result of experiment

實驗中，走路速度加快后將產(chǎn)生跑步誤判，跑步速度加快會被誤識別為跳躍；若跳躍幅度小則會產(chǎn)生跌倒誤判或者跑步誤判，而跌倒速度大將產(chǎn)生跳躍誤判，實驗結果與常識相符。

4　結束語

本文基于人體行為建立四維數(shù)據(jù)采集空間模型，給出了非線性系統(tǒng)下的過程狀態(tài)方程和測量方程。根據(jù)傳感器信噪比和信任級別針對此模型提出了有效的人體行為識別算法。實驗結果表明，系統(tǒng)算法可對數(shù)據(jù)的進行有效處理，數(shù)據(jù)處理后更加平滑和準確，可對人體行為進行有效識別。在系統(tǒng)識別過程中對魯棒性影響較大的數(shù)據(jù)將出現(xiàn)在跳躍、跌倒等加速度數(shù)據(jù)變化近似的行為中，當走路、跑步、跳躍和跌倒速度變化過大時，將產(chǎn)生系統(tǒng)誤判。如何進一步提高系統(tǒng)穩(wěn)定性和擴展對人體其他行為的識別是下一步研究重點。

［1］甘玲，陳頫．人體行為分析方法的研究與仿真［J］．計算機仿真，2013，9（30）：419-423．

［2］楊宏，吳旭光．卡爾曼濾波算法在多傳感器融合技術中的應用［J］．彈箭與制導學報，2009，5（29）：251-254．

［3］谷軍霞，丁曉青，王生進．基于人體行為3D模型的2D行為識別［J］．自動化學報，2010，1（36）：46-53．

［4］梁丁文，袁磊，蔡之華，等．基于無跡卡爾曼濾波傳感器信息融合的車輛導航算法［J］．計算機應用，2013，33（12）：3444-3448．

［5］石欣，熊慶宇，雷珞寧．基于壓力傳感器的跌倒檢測研究［J］．儀器儀表學報，2010，31（3）:66-70．

［6］D M Karantonis，M R Narayanan，M Mathie，etal．Implementation of a real-time human movement classifier using a 3-axial accelerometer for ambulatory monitoring［J］．IEEE Transactions on Information Technology in Biomedicine，2006，10 （1）:156-167．

［7］趙海勇，李程友．基于多特征融合的運動人體行為識別［J］．計算機應用研究，2012，29（08）3169-3172．

［8］M N Nyan，F(xiàn)rancis E H TAY，M Manimaran，etal．Garmentbased detection of falls and activities of daily living using 3 axis MEMS accelerometer［J］．Journal of Physics:Conference Series，2006（34）:1059-1067．

［9］Mebekse Aydin，Metin Gokasan，Seta Bogosyan．Fuzzy based parameter tuning of EKF observers for sensorless control of induction motors［J］．IEEE SPEEDAM，2014（10）:174-1179．

［10］WANG Xingbo，WANG Xiaotao，ZHANG Huanshui．Target tracking in wireless sensor networks using sequential implementation of the extended kalman filter［J］．IEEE Chinese Automation Congress（CAC），2013:132-137．

Activity events recognition algorithm based on extended Kalman filter

REN Zi-liang，QIN Yong，LI Zhi-xiong
（School of Computer，Dongguan University of Technology，Dongguan523808，China）

By studying the model of multi-sensor data acquisition and Kalman filter，a new nonlinear algorithm for human action recognition is proposed in this paper.The acceleration sensor data is mapping to a three-dimensional space，which combined with pressure sensor data to form the four-dimensional data space.Then，the extended Kalman filter is used to process the combined data and revise the processed data.After that，system identifies human action based on trust level and weight fusion.The simulation results demonstrated that the algorithm can improve the accuracy of the sensor and effective identify the human action.

sensors data；human action；extended Kalman filter；optimization algorithm；weight fusion

TN911.23

A

1674－6236（2016）02-0015-03

2015-04-07稿件編號：201504056

廣東省教育廳科技創(chuàng)新項目（2013KJCX0178）；東莞市科技計劃項目基金（2012108102007）

任子良（1984—），男，河南汝州人，碩士。研究方向：傳感器網(wǎng)絡、信號重構與盲源分離。