基于GPS/GLONASS星座衛星的星間GDOP最小值分析

肖 寅，姜興龍，龔文斌，沈學民

（1．上海技術物理研究所 上海 200083；2．上海微系統與信息技術研究所 上海 200050；3．上海微小衛星工程中心 上海 201203）

基于GPS/GLONASS星座衛星的星間GDOP最小值分析

肖 寅1，3，姜興龍2，3，龔文斌3，沈學民1，3

（1．上海技術物理研究所 上海 200083；2．上海微系統與信息技術研究所 上海 200050；3．上海微小衛星工程中心 上海 201203）

衛星自主定軌時選擇測量衛星的幾何構型對于定軌精度有著重要的影響，其影響程度由GDOP（幾何衰減因子）來決定。GDOP值的下限限制了在一定的測量精度下的自主定軌精度。通過分別構建GPS星座和GLONASS星座并分析其構型特征，確定了接收機GDOP取理論最小值時的邊界條件，利用均勻采樣法分別得到GDOP的理論最小值，同時進一步用仿真數據驗證了兩者理論值的正確性。

自主導航；GDOP；均勻采樣；衛星星座

GPS系統和GLONASS系統是目前全球四大衛星導航系統中發展歷史最久，最具代表性的兩個，同時兩大系統理論上各自都可以構成星間鏈路，通過星間雙向測距以達到衛星在長時間得不到地面系統支持的情況下自主導航的功能。

在星間雙向測距中選擇哪些導航衛星作為測量對象是建立星間鏈路的關鍵技術之一，其中一個重要的選擇指標就是GDOP值的大小。這是因為GDOP代表從測量誤差的標準差到用戶接收機位置解的放大量。如果選擇的衛星使這個值較小，那么測量誤差的放大量就小，從而使導航衛星的定位比較精確。因此，找到GDOP的最小值以及接近這個值的衛星幾何構型對于在自主導航的情況下提高導航衛星自身的定軌精度具有重要的意義。

不同的星座構型限制了導航衛星可以選擇星間測量的衛星范圍，從而使其能夠達到的GDOP值范圍也不同。文中首先通過STK仿真軟件構建了GPS/GLONASS導航星座系統，分別確定了兩大導航星座中任意兩顆可見衛星的俯仰角范圍，即計算理論GDOP最小值的邊界范圍；然后將其引入到地面接收機GDOP的計算公式，進而得到星載接收機理論GDOP最小值的計算方法及邊界條件，并用均勻采樣法得到在四顆衛星情況下兩大系統GDOP值的理論下限；最后通過仿真得到的軌道數據計算出GDOP最小值，驗證了理論最小值的正確性。

1　建立GPS/GLONASS仿真模型

STK的全稱是Satellite Tool Kit（衛星軟件工具包），是由美國AGI公司開發的一款在航天工業領域應用的商業化分析軟件。它作為一種可以方便快捷地分析復雜的陸、海、空、天、電（磁）任務的專業仿真平臺，能夠提供簡單易懂的圖表和文本形式的分析結果，來確定最優方案［1］。

在STK中設置表1中的衛星軌道參數，構成GPS和GLONASS兩個導航系統的Walker星座。

仿真建立的GPS星座和GLONASS星座的平面圖如圖1所示。

表1　GPS/GLONASS軌道參數Tab.1　Orbit parameters of GPS/GLONASS

根據STK產生的軌道坐標分別確定GPS/GLONASS系統每兩顆衛星的俯仰角范圍。GLONASS星座的星間俯仰角范圍為0．679°～75．527°；GPS星座的星間俯仰角范圍為10．381° ～76．112°。

2　GDOP的定義

GDOP是幾何因子，它代表從測量誤差的標準差到解的放大量，其值僅僅是衛星/用戶幾何布局的函數。對j顆衛星進行偽距測量，得到偽距測量誤差與位置誤差的關系［2］，寫成矩陣形式為：

圖1　GPS/GLONASS星座分布Fig．1　The satellite constellation distribution of GPS/GLONASS

其中axj，ayj和azj各項表示接收機近似位置指向第j顆衛星的單位矢量的方向余弦。

其最小二乘解為 Δx=（HTH）-1HTΔ ρ，其協方差陣為，得到

其中

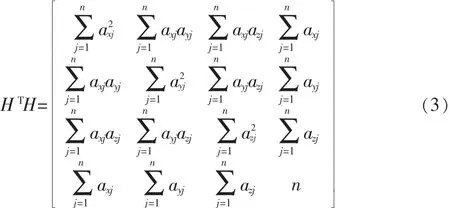
3　GDOP最小值計算分析

導航衛星的接收機與地面接收機在選星方案中有相似之處，也有區別之處。相似之處在于，地面接收機可以到衛星信號的俯仰角不能小于0°，這是因為接收機位于地球球面之上，低于0°的衛星是不可見的。導航衛星可以接收到其他導航衛星信號的俯仰角也不能小于0°，這是因為導航衛星都是分別處于一個半徑（這個半徑就是衛星的軌道高度加上地球的半徑）相同球面之上，我們沿著其中一顆衛星的質點做這個球面的切面，就會發現所有的導航衛星都處于這個切面一側，另一側無導航衛星。不同之處在于收到星座構型的影響和地球遮擋的原因，星間俯仰角范圍受到了進一步的限制。

下面根據文獻［5］的方案對H矩陣進行分塊，令HTH=

當n=4時，可構造如下解：

這一組解的幾何意義是接收機與被測量衛星構成一個六面錐，接收機位于錐頂位置。接收機與其中兩顆被測量衛星構成的平面正交于這個接收機與另外兩個被測量衛星構成的平面。式子中的α，β角分別是接收機指向被測量衛星的連線與Z軸（指向地心）的夾角，即π/2-θ（θ為接收機本體坐標系中其他被測量衛星的俯仰角）。

將上式代入到GDOP公式中，可以得到

4　GDOP最小值解算驗證

對于GPS星座，通過仿真得到每兩顆衛星之間的俯仰角最小值范圍為10．4°至76．1°，由此可得10．4°＜α，β＜76．1°。則

對于該二元函數的條件極值問題，本文采用均勻采樣方法，將（8）式中的α，β劃分為的64×64的網格，在網格中步進為1°均勻采樣后計算，得到GDOPmin=1．915。結果如圖2所示。

同理可知對于GLONASS星座，其邊界條件為14．5°＜α，β＜89．3°，α≠β，計算得GDOPmin=1．724，如圖3所示。

下面根據STK生成的衛星在24小時內的星歷求出H矩陣數值，通過公式（6）分別計算兩個星座系統每300 s步進條件下任意4顆衛星與初始衛星的GDOP的最小值。GPS星座的仿真最小值為2．464，而GLONASS星座的仿真最小值為2．225，如圖4所示。

圖2　GPS星座星間GDOP理論最小值Fig．2　The theoretical minimum value of GDOP for GPS

圖3　GLONASS星座星間GDOP理論最小值Fig．3　The theoretical minimum value of GDOP for GLONASS

圖4　建模仿真計算GDOP最小值Fig．4　The simulation minimum value of GDOP for GPS/GLONASS

通過圖4我們可以看到，由于受到軌道面和衛星相位差的原因，GPS和GLONASS仿真得到的GDOP最小值都是小于理論最小值的，并且GPS仿真最小值大于GLONASS仿真最小值，這也與二者的理論最小值關系保持了一致。

5　結束語

本文構建了 GPS/GLONASS衛星星座模型，對星間GDOP最小值進行了分析和推導，當接收機在n顆衛星的空間幾何分布滿足一定條件時，GDOP達到最小值，得到了4顆衛星鏈路條件下GDOP理論公式。得出了兩個星座GDOP最小值計算的邊界條件，并利用均勻采樣法求得了此值。最后通過生成的星歷數據遍歷整個星座求得該星座的GDOP仿真最小值，驗證了限定邊界條件下的理論最小值的正確性。

［1］高晉寧，方源敏．基于STK的GLONASS系統與GPS系統DOP值的仿真分析［J］．科學技術與工程，2011，11（15）:3384．

［2］Elliott D Kaplan，Christopher J，Hegarty．Understanding GPS: principles and applications［M］．Artech House Inc．2006．

［3］Yarlagadda Ali，ADhahirN．GPS GDOP Metric［J］．IEE Proceeding，Radar，SonarNavigation，2000，147（5）: 2592264．

［4］盛琥，楊景曙，曾芳玲．偽距定位中的GDOP最小值［J］．火力與指揮控制，2009，34（5）:22-24．

［5］陳坡，韓松輝．衛星導航中GDOP最小值的分析與仿真［J］．彈箭與制導學報，2013，34（5）:1-5．

［6］叢麗，Ahmed I Abidat，談展中．衛星導航幾何因子的分析與仿真［J］．電子學報，2006，34（12）:2204-2208．

［7］叢麗，談展中．提高衛星導航定位精度和實時性的選星算法［J］．系統工程與電子技術，2008，30（10）:1914-1917．

［8］YANG Yong，MIAO Ling-juan．GDOP results in all-in-view positioning and in four optimum satellites positioning with GPS PRN codes ranging［C］//IEEE Position Location and Navigation Symposium，2004:723-727．

［9］WU Chih-Hung，HO Va-Wei．Genetic Programming for the Approximation of GPS GDOP［C］//Proceedings of the Ninth InternationalConferenceonMachineLearningand Cybernetics，Qingdao，2010．

［10］Sairo H，Akopian D，Takala J．Weighted dilution of precision as quality measure in satellite positioning［J］．IEE Proc．-Radar Sonar Navig．，2003，150（6）:430-436．

Analysis of GDOP minimum value for autonomous navigation based on GPS/GLONASS constellation

XIAO Yin1，2，JIANG Xing-long2，3，GONG Wen-bin3，SHEN Xue-min1，3
（1．The Shanghai Institute of Technical Physics，Shanghai 200083，China；2．Shanghai Institute of Microsystem and Information Technology，Shanghai 200050，China；3．Shanghai Engineering Center for Microsatellites Shanghai 201203，China）

Geometry of measuring satellites has important implications for precision of the autonomous orbit determination．Currently，the affecting of the geometry for terrestrial receiver and a navigation satellites on the positioning precision is mainly measured by the GDOP．The lower limit of GDOP limits the measurement accuracy of a positioning accuracy range of the user．Constructing navigation constellation of GPS and GLONASS determines the boundaries for taking the minimum value of GDOP of the terrestrial receiver．Using uniform sampling get the minimum GDOP．Simultaneously，the simulation data verified the correctness of the minimum GDOP．

autonomous navigation；GDOP；uniform sampling；satellite constellation

TN961

A

1674－6236（2016）02-0021-04

2015-03-13稿件編號：201503191

肖 寅（1986—），男，湖北武漢人，博士研究生。研究方向：導航衛星自主導航技術。