基于二階帶通濾波器的加速度計結構化動態建模

楊子凱，王建林，于 濤，趙利強

（北京化工大學 信息科學與技術學院，北京　100029）

基于二階帶通濾波器的加速度計結構化動態建模

楊子凱，王建林，于 濤，趙利強

（北京化工大學 信息科學與技術學院，北京100029）

針對加速度計二階動態模型難以準確描述較高頻域范圍內加速度計動態特性的問題，文中提出了一種基于二階帶通濾波器的加速度計結構化動態建模方法。該方法以加速度計二階動態模型為基礎，將二階帶通濾波器作為基本單元對加速度計動態模型的結構進行修正，實現加速度計動態模型的結構化升階，建立加速度計高階動態模型。實驗結果表明，該方法所建立的加速度計高階動態模型相對于二階動態模型具有更高精度，能更好地描述加速度計的動態特性。

加速度計；結構化動態建模；二階帶通濾波器；頻率響應特性

加速度計動態模型是描述加速度計動態特性的主要方法之一，是分析研究加速度計動態誤差補償、動態解耦的基礎［1］?，F有的加速度計動態建模方法中，將加速度計等效為單自由度彈簧－質量－阻尼器系統，用二階動態模型來描述加速度計的特性，并通過最小二乘法等參數模型辨識方法估計二階動態模型的參數。胡紅波等［2］結合絕對法沖擊動態校準加速度計的實驗數據，利用線性最小二乘算法在頻域內實現了加速度計二階動態模型參數的估計；Alfred Link等［3］利用狀態空間描述加速度計輸入輸出及噪聲之間的關系，提出了一種加速度計輸入信號的處理方法，結合加速度計的沖擊響應，通過極小化系統預測誤差序列實現了加速度計二階動態模型參數的估計；Alfred Link等［4-5］利用加速度計正弦校準測量的數據和線性最小二乘算法以及加速度計沖擊校準測量的數據和頻域加權最小二乘算法辨識得到了加速度計二階動態模型的參數。這些方法所建立的加速度計二階動態模型具有較高精度，在較低頻域范圍內能較好的描述加速度計的動態特性，然而在較高頻域范圍內二階動態模型難以對加速度計動態特性進行準確描述。二階帶通濾波器可以允許指定頻域范圍內的信號通過，同時阻止低于或高于該頻域范圍的信號干擾或噪聲，加速度計的頻率響應特性可以看作是二階系統頻響特性與一個或多個二階帶通濾波器頻響特性的疊加。

文中以加速度計二階動態模型為基礎，提出了一種基于二階帶通濾波器的加速度計結構化動態建模方法，利用二階帶通濾波器實現加速度計動態模型結構化升階，建立加速度計高階動態模型，更加準確地描述加速度計的動態特性。

1　加速度計動態模型

1.1加速度計二階動態模型

在測量運動體的加速度時，加速度計緊密固定在被測運動體上，與被測運動體加速度相同，此時，加速度計可等效為單自由度彈簧－質量－阻尼器系統［3］，如圖1所示。

加速度計單自由度彈簧－質量－阻尼器系統的輸入輸出微分方程為

圖1　單自由度彈簧－質量－阻尼器系統Fig．1　The one degree of freedom spring-mass-damper system

1.2加速度計動態模型結構化升階

二階帶通濾波器的傳遞函數可表示為

式中，ω0為帶通濾波器的中心角頻率；帶通濾波器的帶寬B0=ωh-ωl；ωh，ωl分別為上下限截止角頻率，Av是帶通濾波器在中心角頻率ω0處的增益。

1）加速度計高階動態模型構建方式

圖2給出了加速度計高階動態模型的構建方式。

圖2　加速度計高階動態模型的構建過程Fig．2　The building process of higher-order dynamic model of accelerometer

圖2所示加速度計高階動態模型構建過程是一個串聯結構，經過i-1個串聯環節后所得模型Gi（s）可表示為：

式中，G0（k-1）（s）為第 k-1個串聯環節中二階帶通濾波器的傳遞函數 G0（s）；G1（s）為加速度計二階傳遞函數模型，對式（1）所示加速度計二階微分方程模型作拉普拉斯變換，可得

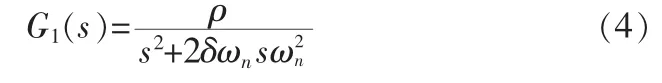
2）加速度計動態模型迭代結構化升階

經過次結構化升階后所得加速度計動態模型Gi（s）為：

式（5）中動態模型的結構和參數都已知，加速度計動態模型中只有二階帶通濾波器的3個參數未知，因此為了得到完整的加速度計動態模型Gi（s），需要估計二階帶通濾波器的參數。模型Gi-1（s）有如下關系：

式中，Ui-1（s）表示模型Ui-1（s）預測輸出的拉普拉斯變換；A（s）表示加速度計輸入加速度信號的拉普拉斯變換。

由式（5）和式（6）可得加速度計動態模型Gi（s）中二階帶通濾波器G0（s）有如下關系表達式

式中，U（s）為加速度計輸出電壓信號的拉普拉斯變換。

利用模型的輸出誤差數據及預測輸出數據辨識模型Gi（s）中二階帶通濾波器G0（s）的參數，就可建立完整的加速度計動態模型Gi（s）。

2　加速度計動態模型參數辨識

加速度計高階動態模型的參數辨識，首先需要辨識加速度計二階動態模型的參數；然后根據式（7）所示的關系式，利用參數模型辨識方法辨識加速度計高階動態模型［6］中二階帶通濾波器的參數。

2.1加速度計二階動態模型參數辨識

式（1）所示加速傳感器二階微分方程對應的狀態空間方程為

采用零階保持器對式（8）進行離散化，可得加速度計的離散狀態方程為

引入前向移位因子q，有qa（k）=a（k+1），可得：

式中，θ=［δ，ωn，ρ］T為待辨識的3個參數。

由式（10）可得如下差分方程：

根據式（11）所示的線性回歸模型結構，可得系統最優一步預測輸出為［8-9］：

系統預測誤差可表示為：

加速度計二階動態模型的參數θ可通過極小化如下誤差準則函數進行估計［6］：

2.2二階帶通濾波器參數辨識

根據式（7）所示加速度計動態模型Gi（s）中二階帶通濾波器G0（s）關于Ui-1（s）和U（s）的關系表達式，令Ei-1（s）=U（s）-Ui-1（s），可得：

式中，N為采樣數據點總個數，ZN為系統輸入輸出數據集。

式（14）所示誤差準則函數的極小化求解，可利用最小二乘算法實現，參數θ的估計值可表示為

對式（16）作反拉普拉斯變換可得二階帶通濾波器的微分方程為：

根據上述加速度計二階動態模型參數辨識方法，亦可用最小二乘法實現加速度計高階動態模型中二階帶通濾波器參數的辨識。

3　實驗與分析

3.1加速度計二階動態模型辨識結果

文中實驗獲取加速度計絕對法沖擊動態校準實驗數據的校準裝置是采用中國計量科學研究院的沖擊激勵系統。由輸入加速度峰值am=4 950．00 gn（gn=9．81 m/s2）的實驗數據進行辨識計算，可得到加速度計二階動態模型的三個參數分別為δ=0．446 9，ωn=2．317 5×105rad/s，ρ=κη=1．145 8×106。圖3給出了辨識所得加速度計二階動態模型的頻率響應曲線與輸入加速度信號峰值am=6036．16gn的實驗數據經過經驗傳遞函數估計（Empirical Transfer Function Estimate，ETFE）方法［3］計算得到的加速度計頻率響應曲線的對比結果［10］。

圖3　加速度計頻率特性曲線對比圖Fig．3　Comparison chart of frequency characteristic curve of accelerometer

由圖3辨識所得加速度計二階動態模型的頻率響應曲線與實驗數據經過ETFE方法計算得到的加速度計頻率響應曲線的對比結果可以看出，兩種不同方法得到的頻率響應曲線在較低頻域范圍內具有良好的一致性，而在較高頻域范圍內存在較大差異。

3.2加速度計高階動態模型辨識結果

1）一次結構化升階

利用加速度峰值am=4950．00gn的實驗數據，根據加速度計二階動態模型的 3個參數，通過式（11）所示差分方程計算得到加速度計二階動態模型的預測輸出，同時利用加速度計實測輸出數據求得加速度計二階動態模型對應的輸出誤差數據。結合獲得的數據，利用最小二乘法辨識得到二階帶通濾波器的3個參數分別為ω0處的增益Av=0．080 7，帶寬B0=3．508 2×106rad/s，中心角頻率ω0=6．264 9×105rad/s。由此可得經過一次結構化升階后所得高階動態模型G2（s）的傳遞函數為

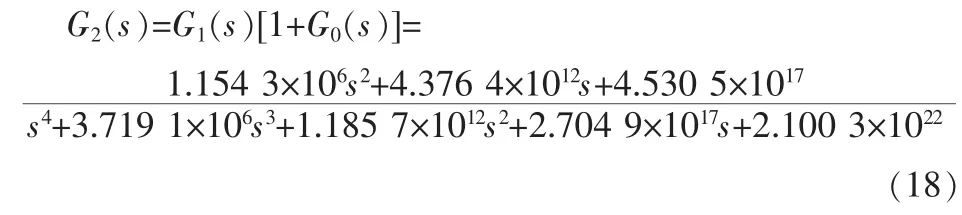
改進后所得加速度計動態模型與二階動態模型的頻率響應曲線對比結果如圖4所示。

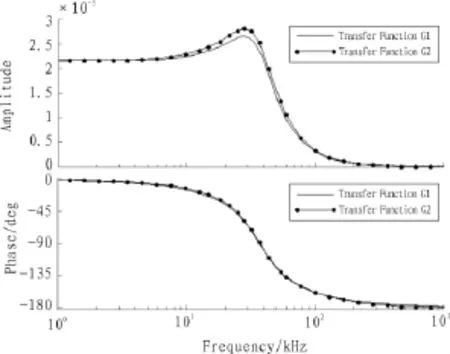
圖4　加速度計動態模型的頻率響應曲線Fig．4　The frequency domain response curve of dynamic model of accelerometer

由圖4可以看出，相比于二階動態模型，一次改進后所得加速度計動態模型的幅頻響應有較明顯的改進，能更好描述加速度計的動態特性。

2）加速度計高階動態模型分析

表1給出了經過0～4次結構化升階后所得加速度計動態模型幅頻響應與ETFE計算值的誤差平方和。

由表1中所示不同階次動態模型對應的幅頻響應誤差平方和可以看出，經過一次修正后，所得模型對應的幅頻響應誤差平方和相比于二階動態模型有較明顯的減??；然而繼續對模型作2～4次修正后，所得動態模型對應的幅頻響應誤差平方和相比于作一次修正后所得模型沒有顯著的減小，因此，只需要對加速度計二階動態模型作一次結構化升階，過高階次的模型對于加速度計動態特性的描述沒有實際有效的意義。

表1　加速度計動態模型對應的誤差平方和Tab.1　The sum of error square of amplitude frequency values of accelerometer dynamic models

4　結　論

本文所提出的基于二階帶通濾波器的加速度計結構化動態建模方法，以二階動態模型為基礎，利用二階帶通濾波器實現加速度計動態模型結構化升階，建立加速度計高階動態模型，能更好描述加速度計的動態特性。

［1］俞阿龍．基于遺傳神經網絡的加速度傳感器動態建模方法［J］．儀器儀表學報，2006，27（3）:315-318．

［2］胡紅波，孫橋．基于絕對法沖擊校準的加速度計參數辨識研究［J］．測試技術學報，2013，27（1）:19-24．

［3］Link A，Von Martens H J．Accelerometer identification using shock excitation［J］．Measurement，2003，35（2）:191-199．

［4］Link A，T?ubner A，Wabinski W，et al．Calibration of accelerometers:determination of amplitude and phase response upon shock excitation［J］．Measurement Science and Technology，2006，17（7）:1888-1894．

［5］A．Link，A．T?ubner，W Wabinski，et al．Modelling accelerometers for transient signals using calibration measurements upon sinusoidal excitation［J］．Measurement，2006，40 （9）:928-935．

［6］徐逢秋，徐安螢，袁?。环N程控濾波器的設計［J］．電子設計工程，2010（7）:198-199．

［7］肖德琴，馮健昭，周權，等．基于高斯頒布可傳感器網絡信譽模型［J］．通信學報，2008（3）:47-53．

［8］Ljung L．System Identification［M］．2nd ed．New Jersey Englewood Cliffs:Prentice-Hall，1998．

［9］Ljung L．Prediction error estimation methods［J］．Circuits，Systems and Signal Processing，2002，21（1）:11-21．

［10］田之俊，王敏．基于FPGA的高階音頻均衡濾波器設計［J］．電子科技，2011（2）:4-6．

Structural dynamic modeling of accelerometer based on second-order band-pass filter

YANG Zi-kai，WANG Jian-lin，YU Tao，ZHAO Li-qiang
（College of Information Science and Technology，Beijing University of Chemical Technology，Beijing 100029，China）

For the second-order dynamic model of accelerometer cannot accurately describe the dynamic characteristics of accelerometer on the higher frequency-domain，a structural dynamic modeling method of accelerometer based on second-order band-pass filter is proposed．The method takes the second-order pass filter as basic unit to achieve the dynamic model of accelerometer structural ascending order based on the second-order dynamic model of accelerometer，in order to build the high-order structural dynamic model of accelerometer．Comparing with the second-order dynamic model，experimental results show that the high-order dynamic model of accelerometer has higher accuracy，and can better describe the dynamic characteristics of accelerometer．

accelerometer；structural dynamic modeling；second-order band-pass filter；frequency response characteristics

TN713+．5

A

1674－6236（2016）02-0072-04

2015-05-09稿件編號：201505078

國家重大科學儀器設備開發專項項目(2012YQ090208)

楊子凱（1988—），男，四川廣元人，碩士研究生。研究方向：加速度計動態建模。