在操作中建構數學模型

江蘇南通市港閘區唐閘小學 郭 祥

在操作中建構數學模型

江蘇南通市港閘區唐閘小學 郭 祥

《義務教育數學課程標準》（2011年版）明確地將“模型思想”列為核心概念之一，這是當今社會對義務教育階段的數學教學提出的新課題和新要求。在廣義模型觀下，數學就是關于模型的科學，學生的數學學習本質上就是對數學模型的認知以及建模過程的經歷與經驗的積累。數學模型的抽象性與小學生以形象思維為主的認知特征，是數學建模教學中一對突出的矛盾，化解矛盾的方法是多元的。其中，通過學生實踐操作化解矛盾，效果顯著。

一、在操作中誘發模型意識

著名教育學家蘇霍姆林斯基曾說過：“兒童的智慧就在他的手指尖上。”那么，由“指尖”抵達“智慧”的通道是什么呢？讓學生面對現實的數學問題，在內心產生疑惑與探究的欲望，積聚操作的內驅和勢能，讓操作成為學生內心深處的一種需求，而不是外在的指令要求，是一則良策。

如《三角形三邊關系》的教學，三角形是由三條線段圍成的圖形，反過來，提供三條線段是不是就一定能圍成一個三角形呢？對此，學生或肯定，或否定，或心存疑惑，此時用小棒替代線段來圍一圍的操作自然成為學生驗證自己內心想法的一種強烈需要。在選擇長短不同的小棒圍三角形的嘗試中，學生會主動發現：同樣是三條線段，有時能圍成三角形，有時則不行。這是為什么呢？操作結果勢必誘發新的探索：“怎樣的三條線段才能圍成三角形呢？怎樣的則圍不成？”學生的探索自然會匯聚到一點——三角形三邊關系的數學模型上。從4厘米、5厘米、6厘米和10厘米的四種小棒中，選擇三根小棒動手操作、觀察記錄和比較交流，發現三角形任意兩邊長度的和大于第三邊。

顯然，真正建立在學生內在需求基礎上的數學活動，能夠有效誘發學生對數學模型的思考與探索；翔實的操作體驗和深層的認知需求協同作用下的數學活動，是學生主動建構數學模型的一條重要途徑。

二、在操作中豐富模型體驗

概念作為一種數學模型，尤為抽象，學生不易理解，難以掌握，也容易混淆。教學時，教師應盡量將抽象的概念做具體的、形象化的演繹，將靜態的描述轉化為動態的操作過程，讓學生的思維發源、依托并超越操作活動。通過操作獲得直接的感性體驗與認識；在有層次、多維度的操作體驗中逐步豐富表象、感悟屬性；憑借“操作—思維，思維—操作”的不斷往返交替與螺旋上升，助推學生對數學模型的本質領悟與理解。

如《認識周長》的教學，是要引導學生在二維平面圖形中研究一維長度的概念，對學生而言具有認知上的挑戰，其關注點和思維都難以聚焦，認識也難以清晰、到位和深刻。需要引導學生利用并順應先前認識圖形的經驗與順序——由體到面，做進一步的遞推，再由面到線逐步建立起一周邊線長度——周長的概念。教學中應引導學生經歷一些必要的操作活動，借助學生熟悉的素材體驗“做中學”。首先，讓學生把自己喜歡的卡通貼畫的邊緣描一描，并從卡片上剪下來，剪好后同桌互相指一指、說一說：“你沿著什么剪的？從哪里剪到哪里？卡通貼畫的邊緣，也就是邊線在哪里？”在描、剪、指、說的過程中體會“邊線” “一周”的含義。接著，讓學生在小組里指一指、說一說書本、課桌、樹葉、硬幣等物體表面的“一周邊線”，并且比較它們的長短；再讓學生獨立描一描平面圖形（長方形、三角形、半圓形、不規則圖形）的邊線，幫助學生從實物到平面圖形，完整地建立對 “一周邊線長度”——周長的理解。最后，再設法讓學生量一量樹葉的周長、樹干的周長，在化曲為直，從平面到立體的變式、拓展的操作體驗中，豐富和完善對周長概念的本質理解。

概念教學的兩個關鍵點，一是要讓學生準確把握其內涵，二要讓學生厘清、界定其外延。由于二者往往會交織于概念模型形成的過程之中，常常需要通過分層操作、專項操作讓學生在豐富模型體驗的基礎上完善、深化對模型的認知。

三、在操作中生成模型表征

現代心理學認為，思維的發展一般要經歷“直觀動作思維→具體形象（表象）思維→抽象邏輯思維”這樣三個階段。

學生的操作過程是一種思維的外化過程，常常能夠助推其直覺思維和具體形象（表象）思維；學生在操作過程的體驗，對操作經驗的積累，以及基于操作結果的分析與感悟，常常會內化為他們頭腦中的表象或圖式。隨著表象的不斷豐富和逐步精致化，則會進一步深化為理性經驗和認識，實現圖式表征到意義表征的飛躍。

如《搭配的規律》的教學，出示圖片信息：2件上衣和3條褲子；呈現問題：一件上衣與一條褲子搭配，一共可以有多少種不同的穿法？先讓學生借助實物圖片擺一擺，通過實踐操作獲得直觀經驗；再把自己的想法設法在本子上表達出來；然后合作交流，展示不同的數學思考：有的用文字一一列舉，有的用符號（字母、數字、圖形等）來表達，還有的用連線方式呈現……最后，通過比較、概括達成共識——用連線的方式表達 （如圖1）。這種幾何直觀的圖式兼具形象性和過程性，在后續解決類似于“4個素菜與2個葷菜，1個葷菜搭配1個素菜，有幾種不同的搭配方法”之類的問題時，學生便能運用。

搭配圖式是一種直觀化的操作模型，它還有待于進一步地抽象概括，成為更為上位的具有一般性、概括性的符號化的數學模型。如將上述搭配圖式提升為乘法原理的數學模型：這類圖式還可以用來解決什么問題？如果上例變成20件上衣和30條褲子，運用搭配圖式還方便嗎？能改用一個數學式子來表示嗎？（20×30）此類問題的解決能有一個通用的模式嗎？（a×b）在搭配圖式的運用與拓展中，乘法原理的數學模型水到渠成。

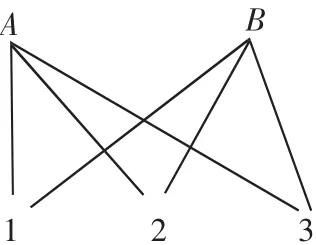
圖1

操作活動常常起始于某個特定的情境和特定的實物，但不能僅僅止于操作過程的經歷和結果的獲得，也不能只停留在直觀感性和直覺思維層面。實施操作活動以后，要有意識地引導學生就自己操作的所獲所感進行個性化的表達交流，通過比較、分析，強化對表象的認知，并利用表象架設橋梁，通過對表象的符號化、數學化，實現操作活動的思維內化，逐步建構學生頭腦中關于操作過程和結果的數學模型。

四、在操作中完善模型建構

學生在操作活動中需要獲得的不僅僅是數學知識和技能，更重要的是經歷探索的過程，學習和掌握研究數學的思維模式與思想方法，體驗知識“再創造”的過程。其間，常常要以操作的階段性結果為基礎，做進一步的分析思考、猜想驗證、交流切磋，實現數學模型的逐步修正、拓展與完善。

如《釘子板上的多邊形》的教學，首先明確研究方向：邊上的釘子數與圖形的面積的關系（如圖2）。然后，通過觀察填表、分析數據，形成階段性研究成果（多邊形的面積是邊上釘子數的一半，即S=n÷2）。接著，學生在釘子板上自由構圖，驗證所發現的規律，并引發沖突（如圖3）：“為什么先前發現的規律在這里不適用了呢？”通過操作、比較發現：當圖內只有1枚釘子時，即當a=1時，S=n÷2。

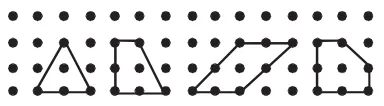
圖2

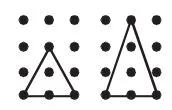
圖3

“當a=2時，多邊形的面積又是多少呢？”小組合作在釘子板上邊圍邊研究。學生運用前期研究成果，遷移先前操作活動經驗，得出當a=2時，S= n÷2+1。據此發散：當a=3、4……時呢，有規律嗎？能一一驗證嗎？需要一一驗證嗎？有什么規律？探索活動從動手操作的有限層面躍升到類比推理的無限境地，學生親身經歷類似數學家研究問題的過程，通過操作、思辨、猜想、驗證、推理活動，自主探究、發現數學，逐步修正、拓展與完善數學模型，獲得“操作—發現—推理”的數學學習與探索的方法啟迪和歷練。

五、在操作中助推模型升級

操作活動不只是單純的“動手”實踐，其核心價值在于對學生數學思維的啟迪與促進，實現外顯動作與內隱思維的雙向互動，促使“操作的思維”和“思維的操作”螺旋上升。以問題解決為行為驅動，以操作過程和階段性結果為思維載體，通過觀察、比較、交流、反思等活動，不斷實現對已有數學模型的創造性改造，逐步創生出新的數學模型。

如《復式統計表》的教學，根據單式統計表（如圖4）進行數據的收集與整理。然后分析數據，回答“哪個興趣小組男生最多？四個興趣小組是男生多還是女生多”等問題時，發現往復觀察、比較的不便，產生組合、重構新的統計表的需求。學習小組在思考中操作，在操作中思考，有的把4張單式統計表縱向排列（如圖5），以解決數據對比不便的問題；有的在將四表第一橫欄合并（如圖6）后，發現數據對比十分方便，但同時產生了數據與組別無法對應、標題如何合而為一等矛盾；有的則更進一步，提出交代男生總數、女生總數以及總人數的設想……學生操作、反思、重構，最終形成復式統計表，從而實現了對數學模型的改造升級。

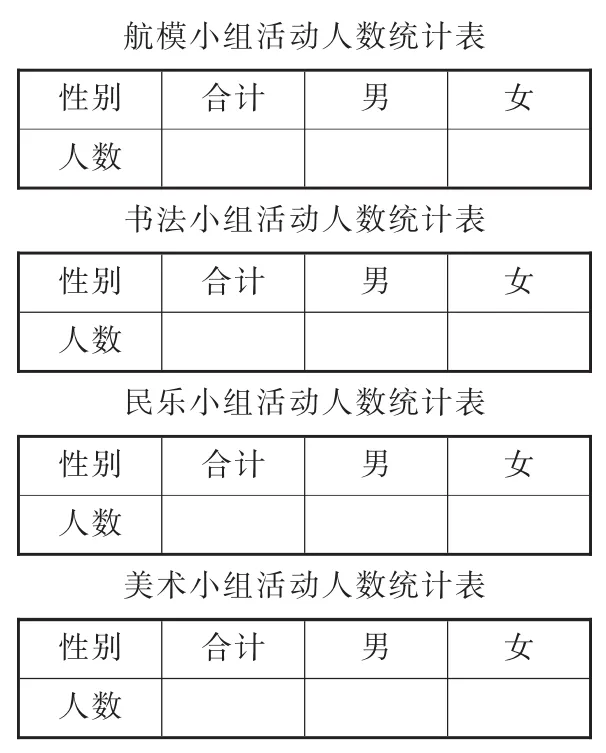
圖4

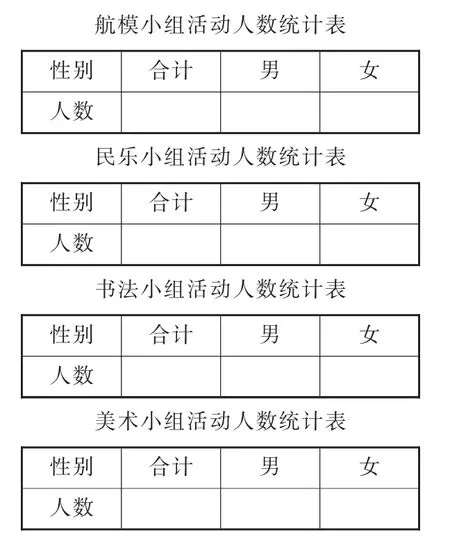
圖5

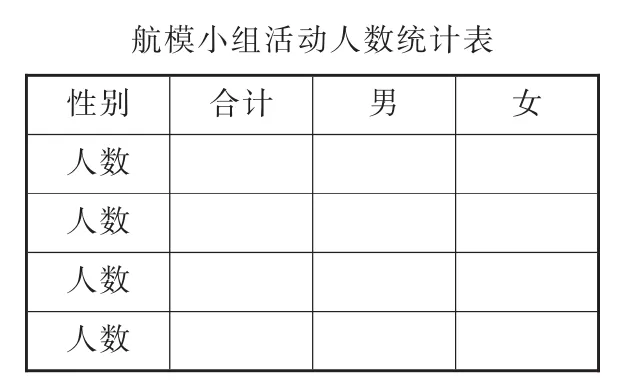
圖6

學生的操作活動應發端于內心深處的實際需要，教師要以適切的問題情境誘發學生產生操作內驅，同時要為學生提供必要的時、空、物等操作平臺，更要設法將教學目標——數學模型的建構，內化為學生解決問題的操作（行為的、心理的）指向。