尾焰輻射強度隨視線方向變化規(guī)律建模與仿真

董健，弓馨

（1.中國科學院長春光學精密機械與物理研究所，長春　130033；2.東北師范大學人文學院，長春　130117）

尾焰輻射強度隨視線方向變化規(guī)律建模與仿真

董健1，弓馨2

（1.中國科學院長春光學精密機械與物理研究所，長春130033；2.東北師范大學人文學院，長春130117）

尾焰紅外輻射強度是導彈預警系統(tǒng)設計所需的重要參數(shù)。根據(jù)尾焰紅外輻射的基本理論以及合理等效，建立了導彈主動段尾焰輻射強度工程計算模型，可用于主動段尾焰輻射強度理論模型的驗證及快速估算預報，在此基礎上建立了尾焰紅外輻射強度隨觀測角度的變化規(guī)律模型，以美國大力神火箭（TITAN II）的實驗結果為參考標準，對比了該模型與其他模型的計算精度，結果表明該模型均方根誤差約是GASL理論模型的1/4，最大誤差約是模型的1/3，并以阿特拉斯導彈（SM-65）和戰(zhàn)斧導彈（BGM-109A）為例進行了仿真，結果符合經驗規(guī)律。

導彈尾焰；紅外輻射特性；工程化模型

導彈尾焰是具有復雜流場結構的非均勻氣體輻射源，其主要成分CO2和H2O是選擇性輻射體，具有不連續(xù)的線狀或帶狀光譜，輻射能量主要集中在2.7μm和4.3μm的輻射帶。核心區(qū)輻射的能量被外圍包圍的溫度較低的混合層吸收，尾焰紅外輻射強度的計算過程就是考慮核心錐的輻射以及外圍混合層的吸收和自發(fā)輻射的過程［1］。

國內外常用的導彈尾焰紅外輻射特性的理論計算方法包括：蒙特卡羅法、反向蒙特卡羅法、六流法、有限體積法和離散坐標法［2］等，并衍生出多種仿真計算軟件：SPF/SIRRM、CHARM等，然而，理論計算模型需要大量的已知參數(shù)［3-5］，各參數(shù)誤差的傳播和積累會使計算結果產生很大的誤差，且由于缺少宏觀參數(shù)對理論計算模型進行表征，難以開展基于試驗測量數(shù)據(jù)的模型參數(shù)校驗工作來進一步提高理論模型的計算精度。

本文在紅外輻射基本理論的基礎上，結合導彈主動段尾焰的特點，對尾焰的投影面積、發(fā)射率等因素進行合理的等效計算，建立了一種導彈主動段尾焰紅外輻射強度的估算模型，可用于理論模型的校驗以及無法建立理論模型時的快速估算預報，并對不同視角下尾焰輻射強度的變化規(guī)律進行了建模仿真，該模型可為紅外預警相機的總體設計提供理論指導與技術支撐。

1　導彈主動段尾焰輻射強度建模

在導彈飛行的主動段，尾焰周圍的溫度場、壓力場是非均勻的，但低溫混合區(qū)的吸收衰減會在很大程度上降低這種非均勻性，從發(fā)動機的噴口開始，可將尾焰分為若干同質層，每層壓力、溫度、流速、分子種類及濃度等參數(shù)相近，若將沿尾焰軸線方向的同質層取加權平均后的溫度作為等效溫度，則可以將尾焰在三維空間內的輻射強度計算近似為對均勻輻射源在等效溫度、等效光學厚度情況下的輻射強度計算。圖1為Titan II火箭尾焰在海拔16公里高度的輻射強度［6］，可見，該曲線的變化規(guī)律與均勻輻射源在某等效溫度下計算的輻射強度規(guī)律基本一致，因此上述假設是合理有效的，下面將在此假設基礎上對導彈主動段尾焰經驗模型進行理論推導。

圖1　Titan II火箭尾焰在海拔16公里高度的光譜輻射強度

對于等效均勻的尾焰輻射場，在某一譜段內光譜輻射強度可表達為：

其中Jv為光譜輻射強度，Iv為平均光譜輻射亮度，A為導彈尾焰在視線方向上的投影面積，簡稱為視線投影面積。

平均光譜輻射亮度Iv可通過下式求得：

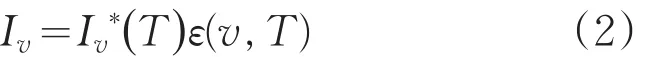
由式（1）、式（2）可得尾焰的光譜輻射強度為：

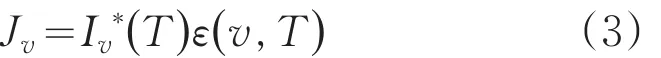
1.1視線投影面積

由于空氣壓力和氣體的濃度的變化，尾焰的大小和形狀隨著高度的變化而變化［7］，如圖2所示，飛行高度在40公里以下的主動段導彈尾焰可視作為圓柱體，其幾何模型可簡化為圖3所示。

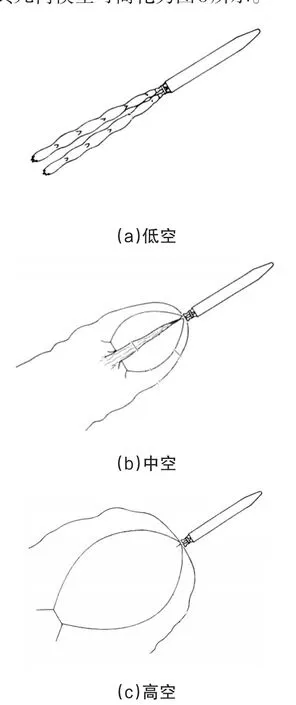
圖2　不同飛行高度導彈尾焰形狀示意圖

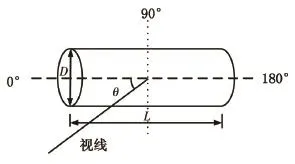
圖3　低空導彈尾焰簡化幾何模型

側視為矩形，后視為圓形，前視為被彈體遮擋的圓環(huán)，其投影面積為：

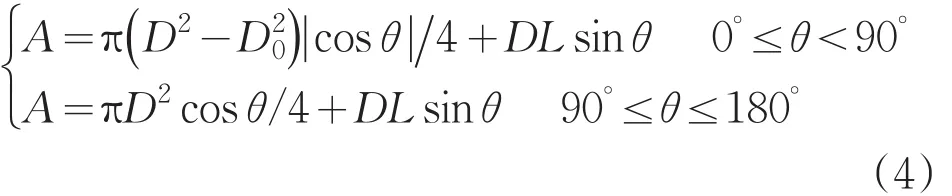
式中D為尾焰等效直徑，D0為彈體直徑，L為尾焰等效長度，θ為視線方向與導彈縱軸的夾角，可通過導彈的俯仰角θe和方位角θa求取：

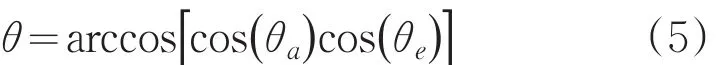
在導彈主動段飛行階段，發(fā)動機尾焰的燃燒質的噴流速度遠遠大于導彈的速度，推力可表示為：

式中F為發(fā)動機推力，P為大氣壓強，Cf為推力系數(shù)，At為發(fā)動機噴口面積。

定義為c與Cf相關的常系數(shù)，故尾焰等效直徑的經驗模型為：

根據(jù)工程經驗，尾焰的有效長度L與排除氣體的馬赫數(shù)Me、尾噴口半徑Rhs、特征軸向比例長度l、渦流混合效率s、環(huán)境自由氣流ρ0和排出氣ρj的密度差相關：

將式（7）、式（8）代入式（4）可得：

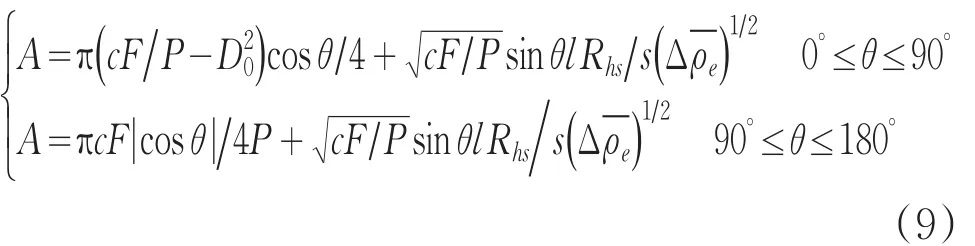
1.2尾焰發(fā)射率

根據(jù)基爾霍夫定律：在一定的波長和溫度下，一個物體的發(fā)射率等于該物體在同溫度、同波長下的吸收率，即發(fā)射率為：

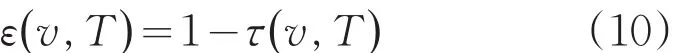
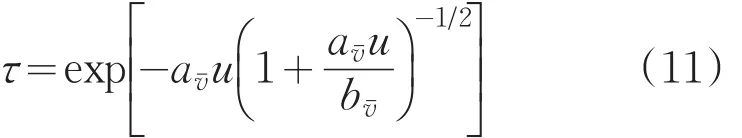
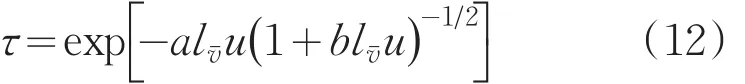
在強線近似和弱線近似的極限下，有：

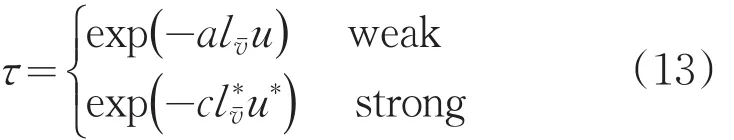
故導彈尾焰的發(fā)射率模型可表示為：

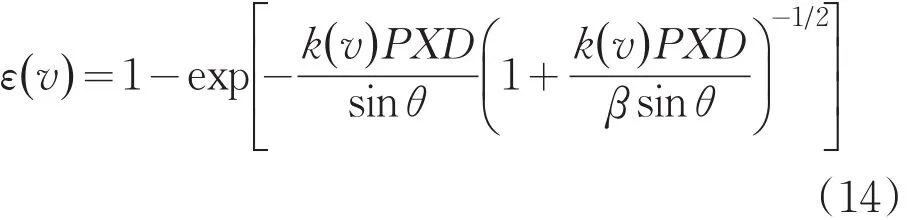
式中k為平均吸收系數(shù)，β為譜線重疊因子，X為輻射氣體的克分子數(shù)，P為大氣壓強，θ為觀測角度。

由于推進劑類型、成分、推力不同，尾焰燃燒輻射的光譜曲線也不同，根據(jù)文獻［6］的分析結果，可將譜線分為四種類型：強連續(xù)譜線（SO）、強非連續(xù)譜線（SN）、弱連續(xù)譜線（WO）、弱非連續(xù)譜線（WN），如圖4所示。

對于常摻雜鋁粉的固體推進劑，尾焰中燃燒質濃度很高，屬于強連續(xù)譜線，發(fā)射率可近似為1。易貯推進劑燃燒產生的大尺寸尾焰，在2.7μm左右譜段內，屬于強非連續(xù)譜線，根據(jù)強線近似，發(fā)射率可表示為：

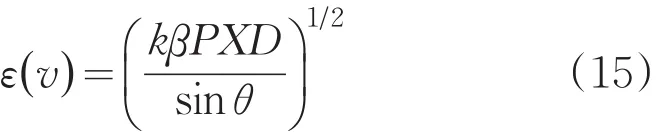
飛行高度較高時的低密度燃燒質、小尺寸、低發(fā)射率尾焰的光譜屬于弱非連續(xù)譜線，發(fā)射率可表示為：

而飛行高度較低時的高密度燃燒質、小尺寸、低發(fā)射率尾焰的光譜則屬于弱連續(xù)譜線，發(fā)射率可由比爾定理表示：

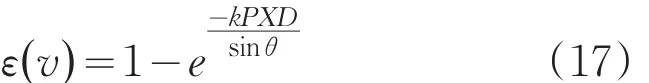
1.3輻射強度隨視線方向變化規(guī)律模型

由式（3）、（9）、（17）可得：

當觀測角0°≤θ≤90°時：

當觀測角90°≤θ≤180°時：

由式（19）可知，導彈主動段尾焰紅外輻射強度與推力、觀測角、推進劑成分、飛行高度、飛行速度等多個參數(shù)相關，模型參數(shù)解耦難度大，但在一定條件下可對模型簡化從而得到輻射強度隨觀測角度的變化規(guī)律。

以正舷側觀察為參考視角，對模型簡化后可得各角度下輻射強度的變化規(guī)律：

當觀測角0°≤θ≤90°時：

當觀測角90°≤θ≤180°時：

對于同型號導彈，彈體直徑D0相同，主動段內尾焰直徑D、長度L可由工程經驗估算，因此，除了具有弱連續(xù)譜線形式尾焰，其他三種譜線形式尾焰的角度特征均可通過上式快速求解，而對于弱連續(xù)譜線形式的尾焰，通過理論模型計算出k、P、X等參數(shù)后，本文模型可用于對理論計算模型的檢驗。

2　模型驗證及仿真

為驗證本文所建立的模型的可靠性，將本文的仿真結果與美國大力神火箭（Titan II）在20km飛行高度各視角下實測的短波紅外測量數(shù)據(jù)、NASA使用的GASL理論模型（General Applied Science Laboratories）的計算結果、文獻［6］中sinθ模型計算結果進行對比，如圖5所示，可見，當觀測角度較大時，三種模型都具有較高的計算精度，但當觀測視角小于8°時，GASL理論模型、sinθ模型的計算結果與實測數(shù)據(jù)相比出現(xiàn)很大差異，當視角為0°，即從尾（頭）部觀察時，sinθ模型計算結果為0，顯然與實際情況不符，本文模型在各視角下均與實測數(shù)據(jù)可以很好地吻合。各模型的計算誤差見表1，可見，本文模型的均方根誤差為0.0347，約是GASL理論計算模型的1/4，誤差最大值為0.0716，約是sinθ模型的1/3，本文模型具有更高的精度，驗證了模型的準確性。

表1　三種模型計算誤差

在導彈紅外預警系統(tǒng)設計中，不同視角下的輻射特性數(shù)據(jù)對于預警圖像仿真分析和目標檢測算法評估具有重要意義［9］，本文對阿特拉斯洲際彈道導彈（SM-65）和戰(zhàn)斧巡航導彈（BGM-109A）主動段紅外輻射強度隨觀測角度的變化情況分別進行了仿真，SM-65采用液體推進劑，彈體直徑3.05米，BGM-109A采用固體推進劑，彈體直徑0.572m，假設在某一飛行高度下尾焰等效直徑分別為15m和7m，等效長度分別為200m和50m，仿真結果如圖6、圖7所示，可見，當視角為90°附近時輻射強度最大，基本沿90°視角對稱，符合經驗規(guī)律。

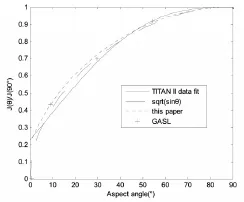
圖5　三種模型計算結果與TITAN II實測數(shù)據(jù)對比

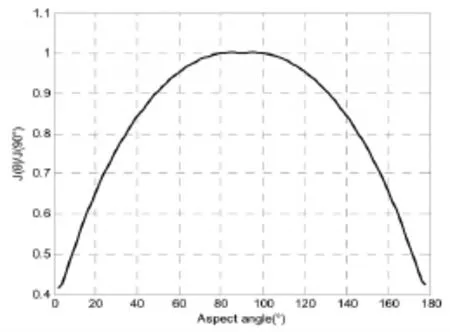
圖6　阿特拉斯（SM-65）導彈尾焰輻射強度隨觀測角變化仿真

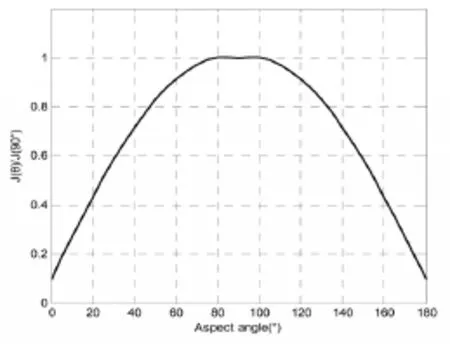
圖7　戰(zhàn)斧（BGM-109A）導彈尾焰輻射強度隨觀測角變化仿真

3　結論

根據(jù)導彈主動段尾焰的形貌特征，建立了尾焰視線投影面積模型，針對不同推進劑類型的導彈尾焰發(fā)射率的不同譜線形式，建立了導彈主動段尾焰輻射強度工程計算模型，可用于理論模型的校驗以及無法建立理論模型時的快速估算預報，建立了尾焰紅外輻射強度隨觀測角度的變化規(guī)律模型，通過與實測數(shù)據(jù)對比分析，表明該模型的均方根誤差約是GASL理論計算模型的1/4，誤差最大值約是sinθ模型的1/3，精度明顯高于其他模型，并且利用該模型對阿特拉斯導彈和戰(zhàn)斧導彈進行了仿真，仿真結果符合經驗規(guī)律，證明該模型對導彈尾焰紅外輻射強度信號的仿真和紅外相機的整體參數(shù)設計有重要的參考價值。

［1］張術坤，蔡靜，楊永軍.尾焰紅外輻射特性的反向蒙特卡羅法模擬［J］.紅外與激光工程，2012，10（12）：2604-2609.

［2］劉尊洋，邵立，汪亞夫，等.復燃對液體火箭尾焰紅外輻射特性的影響［J］.光子學報，2013，42（4）：480-485.

［3］秦蘭琦，汪洪源，張愛紅，等.導彈尾焰流場特性建模與仿真［J］.紅外與激光工程，2014，43（12）：3878-3882.

［4］牛青林，傅德彬，李霞.不同飛行狀態(tài)下固體火箭發(fā)動機尾噴焰數(shù)值研究［J］.航空動力學報，2015，30（7）：1745-1751.

［5］王大銳，張楠，葛明和.液體火箭發(fā)動機尾焰紅外輻射計算方法［J］.導彈與航天運載技術，2015，337（1）：69-73.

［6］Simmons F S.Rocket exhaust plume phenomenology［M］.California：Aerospace Press，2002，145-148.

［7］陳興榮.彈道目標推進段紅外仿真技術研究［D］.南京：南京理工大學，2007.

［8］Liou K N.An introduction to atmospheric radiation ［M］.San Diego：Elsevier Science，1992，6-9.

［9］程軍，張偉，鮑文卓，等.在軌光學相機探測圖像數(shù)字仿真系統(tǒng)的設計與實現(xiàn)［J］.光學 精密工程，2009，17（9）：2136-2144.

Modeling and Simulation of Aspect Dependency Correlation for Exhaust Plumeradiation Intensity

DONG Jian，GONG Xin

（1.Changchun Institute of Optics，F(xiàn)ine Mechanics and Physics，Chinese Academy of Sciences，Changchun 130033；2.College of Humanities，Northeast Normal University，Changchun 130117）

The infrared radiant intensity of missile plume，as an important parameter，has been applied to the designing of space-based early warning system.On the basis of infrared radiant theory and equivalent，an empirical model was built.This model can be used to validate the result of theoretical model and estimate the intensity rapidly.The scaling law was built to show the variation of intensity and aspect angle，the result of this model was compared with GASL model and model referring to TITAN II rocket plumes，it shows that the RMSE of this model is 1/4 than GASL model，the maximum error is 1/3 thanmodel，the simulation results of Atlas SM-65 and Tomahawk BGM-109A meet the empirical regularity.

missile plume；infrared radiant intensity；empirical mode

V231.1

A

1672-9870（2016）03-0073-05

2016-01-04

國家863高技術研究發(fā)展計劃資助項目（2015AA7031082A）

作者簡介：董健（1989-），男，碩士，研究實習員，E-mail：275674705@qq.com