復雜網絡理論在傳統行業中的應用

周其明，劉小園

（1.中國人民解放軍92823部隊，三亞 572021；2.羅定職業技術學院，羅定 527200）

復雜網絡理論在傳統行業中的應用

周其明1，劉小園2

（1.中國人民解放軍92823部隊，三亞 572021；2.羅定職業技術學院，羅定 527200）

隨著近年來復雜網絡的發展，越來越多的研究人員開始用它來解決諸如生命科學與工程等其他領域的問題。目前，復雜網絡理論逐漸滲透到許多不同的學科，也有許多傳統產業正在試圖將復雜網絡理論應用到實際工作中。介紹復雜網絡的基本理論研究，并以人際關系與溝通策略為例，建立在傳統產業復雜網絡的應用模型，并提供解決這些問題的常用方法。

復雜網絡；傳統產業；人際關系；溝通策略

0 引言

目前從神經生物學到統計物理學，網絡已經遍及幾乎所有的科學研究［1］。復雜網絡（Complex Network），是指具有自組織、自相似、吸引子、小世界、無標度中部分或全部特點的網絡。總之，復雜網絡提出了很高的復雜性。其復雜性主要表現在以下幾個方面：

（1）結構復雜性：一個巨大數量的節點，且網絡結構呈現不同的特點。

（2）網絡進化性：節點和連接的不斷出現和消失。例如，在世界范圍內的網絡，任何時間網頁或鏈接都可以打開或關閉，網絡結構在不斷變化。

（3）連接多樣性：不同節點之間的連接權值多樣，且可能存在方向性。

（4）動力學的復雜性：節點集可能歸功于非線性動力學系統，例如，錯綜復雜的時間節點狀態變化。

（5）節點多樣性：在一個復雜的網絡節點可以代表任何東西，例如，在人際關系網絡，一個節點代表一個單獨的實體；在萬維網的網絡，一個節點代表不同的頁面。

（6）多個復雜的融合：更多不可預知的結果間的相互融合。

1 復雜網絡理論

復雜網絡的主要特點是無標度網絡和小世界。

無尺度網絡意味著一個小數量的節點共享大量的連接或大量節點的連接。一般來說，它們滿足Zipf定律（80/20規則，馬太定律）。無尺度網絡缺乏代表平均度值，和節點度波動范圍相當大。無尺度網絡共享一個冪律分布。

小世界網絡的概念是在六度分離的概念上開發，主要是指大部分節點彼此不相鄰，但大多數節點可到達一個小的步數。盡管網絡是大規模的，但任何兩個節點之間存在一個相對較短的路徑。主要是通過測量路徑長度和聚類系數小世界網絡的特點：它有一個小的特征路徑長度和較大的聚類系數［2］。

目前，復雜網絡的研究包括：幾何特性的網絡，網絡的形成機制，網絡演化的統計法，對網絡模型的特點，網絡的結構穩定性和網絡演化動力學機制。在自然科學領域，網絡研究的基本測量包括：程度和分布，特征路徑長度，直徑，密度，介數的網絡，聚類系數，連接矩陣，互惠和冪律。在這里，一些常見的復雜網絡參數將簡要介紹［3］。

1.1 度

度是描述一個最基本的網絡圖，它是一個簡單的單節點性能的重要概念，但在圖論中，度表示一個節點的邊。在有向圖，它可以分為入度和出度。顧名思義，在某種程度上意味著邊緣點為節點，而出度是指該節點指向其他節點的邊數。在某種意義上，一個節點的度數越大，表示該節點有更“重要”的結點權值。

所有的節點度被稱為網絡的平均度。

1.2 特征路徑長度

在網絡中，任選兩個節點，兩個節點之間的最少邊數定義為這兩個節點之間的路徑長度。所有路徑長度平均值是網絡的特征路徑長度。

網絡的特征路徑長度也被稱為平均最短路徑，這是網絡的全局特征，反映了網絡的一般特征。

1.3 密度

密度描述了各點之間關系圖中的貼近。一個完整的圖形是指所有的節點是相鄰的。即使在小型網絡，完整性也是極為罕見的。密度用來衡量總分配的概念邊緣檢測，總密度分布邊匯總來衡量圖的完整程度。

密度測量圖的凝聚力的整體水平。從圖論的角度，密度反映了“緊”的圖。密度取決于兩個參數：網絡結構的包容性和圖形的整體程度。包容是指在圖，即在相關部分節點總數，總結負圖中的孤立節點的數目。密度的計算方法是如下：

其中L表示在圖中的邊的數目，N表示節點的數目。密度在有向圖中的表達：

1.4 直徑

在網絡拓撲結構中，通常兩個節點之間有多個路徑，以最小的步驟路徑作為兩個節點之間的最短路徑。最短路徑的概念是要找到兩個固定的節點之間的最短路徑。在復雜的網絡很難做到，也沒有必要對兩個節點之間的最短路徑做定性分析。一般指對平均距離做定性分析。

整個網絡，這兩個節點之間的最長路徑被定義為網絡的直徑。直徑可與NMB和Pajek計算。

1.5 介數

介數通常分為邊介數和節點介數。

節點介數定義為最短路徑貫穿節點的所有最短路徑比。邊介數定義為最短路徑穿過邊緣的最短路徑比。

介數反映相應節點或邊緣網絡中的作用和影響，這是一個重要的全局幾何形狀，具有很強的現實意義。例如，在人際關系的社會網絡中，介數的分布特征反映了不同的人在整個社會中的地位，這對于發現和保護關鍵人員非常重要。

1.6 聚類集數

假設一個節點有k條邊，在連接的節點，這些k邊緣之間的最大邊數為k（k-1）/2。實際上的邊數與最大數的比值定義為聚類系數。所有的聚類系數的平均值被定義為網絡的聚類系數。聚類系數是一個本地網絡的特點，反映了兩人的朋友圈的重合度，又是朋友的朋友之間的節點度。

1.7 連接矩陣

如果網絡中有n個節點，這些節點之間的連接可以由一個n×n的0-1矩陣來表示。例如，對于一個有向圖的頂點，如果頂點i到頂點j，第i行第j列的值為1，否則其值為0。同樣，如果頂點j點到點i，第j行和第i列的值為1。這樣的矩陣稱為連接矩陣。當有在連接矩陣的幾個非零元素，它是一個稀疏矩陣。在矩陣中的數字1是指一種這n個節點之間的連接。

1.8 互惠

在現代的P2P流媒體技術的應用所建立的模型是通用網狀拓撲結構，并存在著或多或少的同伴和同行之間的互惠行為。例如，在一個有向圖，頂點i可以連接頂點j，并且頂點j可以連接頂點i，那么邊ij是互惠的邊，頂點i和頂點j是互惠點。

一個簡單的方法來獲得一個圖的互惠的邊：bidirected邊和圖中總的邊之比，公式如下：

在這個公式中的分子是圖中bidirected的邊（不包括自環），而M是圖中總的邊（不包括自環），即，

然而，這個簡單的公式往往不能區分高互惠網絡和有很多互惠的連接密度高的隨機網絡，因此我們引入一個更準確的公式來計算互惠邊：

在這個公式中，r是上面定義的互惠邊和有向邊的比率，其計算方法如下：

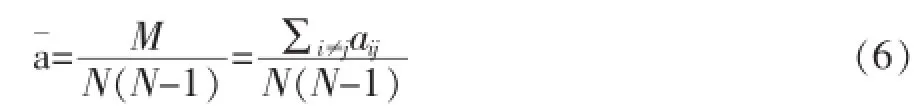
其中N是在網絡的總的節點數。

1.9 度冪律

在許多真實世界的復雜網絡連通度的分布表現出冪函數的形式。K表示節點的度，P（k）表示K的概率密度，冪律分布P（k）～K（-），其中K是大于一個無符號整數，且冪律系數大于1，這是為了確保概率密度的積分收斂從一個無符號整數到無窮大。由于冪律分布無明顯的特征長度，網絡也被稱為無標度網絡。冪律分布廣泛存在于真實世界的大型系統，如互聯網、萬維網、航空網絡、電網、科研合作網絡、生物generegularoty網絡和代謝網絡等。研究人員發現，冪律系數在許多真實世界的復雜網絡是2-3。例如，互聯網絡冪律系數是在2.2-2.48之間，萬維網冪律系數是在2.1-2.45，而代謝網絡的冪律系數約為2.2。

網絡的度冪律分布的一個重要特征是：P（k），節點度K的出現概率exponintially不趨于0時，K的增加，但相對漸近0，由此可知，“長尾巴”的特征，這個首先是在80/20規則和Zipf定律的提出。

網絡的冪律分布表明，有一定數量的度較大的節點，稱為中心。雖然樞紐節點只股票圖形中的一小部分，但它們發揮了重要的作用。由于輪轂的存在，具有完全不同的性格與均勻分布的隨機網絡。

隨機網絡模型假設連接一對節點的概率是相等的，而度分布P（k）是泊松分布。P（k）速度趨于0時，節點K趨于無窮大時是正態分布、指數分布之間的關系。指數分布趨于0時，速度快了，因此我們可以形象的稱為泊松分布的速度。在一般情況下，這三種分布都幾乎是“窄尾”或“無尾”。以最常見的正態分布為例，假設期望值為0，方差為1，則變量的期望值小于方差之間的邊緣的概率是2/3多一點；和它的概率小于兩倍的方差為95%；而概率三倍以上的方差僅為0.3%。這表明，在一個狹窄的范圍內的預期值的變量數的變化，而尾數幾乎是0。因此，只有正態分布與泊松分布一致時，才能反映復雜網絡的特征系統的本質特征。

2 復雜網絡在傳統產業的應用模型

復雜網絡是一個高度抽象的復雜系統的邊和節點的結構。隨著對復雜網絡研究的深入，網絡的拓撲結構、自然的基本理論、演化和解決方案已經證明，對傳統產業提供了新的視野和思路。如果在其他域的元素可以被看作是一個集合的邊和節點，形成一個網絡的拓撲結構，它可以被抽象為復雜網絡模型，并用復雜網絡的理論解決。在本節中，我們采取兩個場景，人際關系與溝通策略，為例介紹了該模型的抽象和解決問題的過程。

2.1 人際關系模型

人際關系模型可以表達為復雜網絡G（V，E），如圖1所示，其參數含義如下：

V：代表復雜網絡中的節點，每個節點代表一人。

E：代表復雜網絡中的邊，每條邊代表有每兩人之間的關系。

W：代表復雜的網絡中邊的權重，Wij表明節點Vi和Vj之間的關系。如兩人之間關系的強度，且在不同的場景有不同的含義。

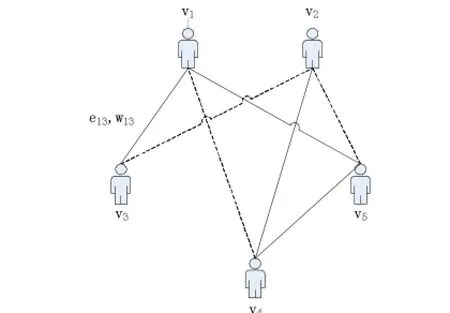
圖1 人際關系的復雜網絡模型

利用上述模型，人際關系問題可以抽象為復雜網絡問題。我們可以用復雜網絡理論解決人際關系的問題，例如，描述某個人的關系，計算出不同關系的強度，預測有些關系的演變等［4］。

2.2 溝通策略模型

基于前面構建的人際關系模式，可以提出交際策略模型［5］。

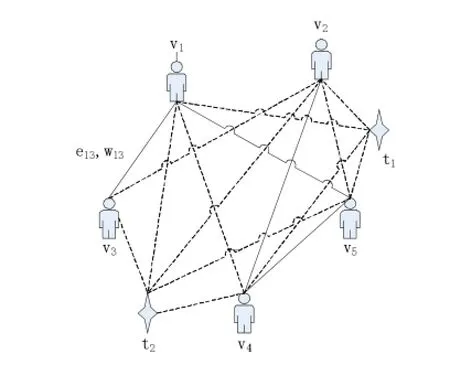
圖2 溝通策略的復雜網絡模型

如圖2所示，ti是指通信塔的位置。選址通信塔需要復雜網絡理論。這些通信塔應確保所有用戶可以被覆蓋，而且使用最少資源。這里的“最少資源”包括以下兩個方面的含義：首先，在保證所有用戶被覆蓋，建造最少的塔；其次，由于通信質量與距離成負相關，盡可能保證塔和用戶之間的總距離最短。這就對應最短路徑算法的問題，其中Dijkstra算法和弗洛依德的最短路徑算法是最流行的。在這里，我們簡要介紹如下：

Dijkstra算法是最典型的最短路徑算法，用來計算從一個節點到其他節點的最短路徑。其主要特點是以起始節點為中心向外擴展，并從它直至結束節點。Dijkstra算法能獲得的最短路徑的最優解，但由于它通過大量的節點，它的效率很低。當網絡是稀疏圖，時間復雜度為O（V2）。

弗洛依德算法主要用于多源最短路徑查找和無負權圖。它使用一個矩陣記錄圖，且時間復雜度為O （V3）。弗洛依德的Warshall算法能對任意兩節點之間的計算出最短路徑，并能正確計算有向圖或負權圖的最短路徑。

3 結語

隨著社會的不斷發展和復雜網絡理論的改進，它已被應用于許多傳統產業。本文在介紹復雜網絡的基本理論的基礎上，提出了可能的應用，如人際關系與溝通策略。事實上，復雜網絡理論可以用在更多傳統的行業，但在建模階段是非常重要的。只有正確的模型，實際的問題才能得到正確地抽象和解決［6］。

［1］Strogatz S H，Exploring Complex Networks［J］.Nature，2001，410（6825）：268-276.

［2］Newman M E J.The Structure and Function of Complex Networks［J］.SIAM Review，2003，45（2）：167-256.

［3］Chunhong Z，Cuibo Y，Xinning Z，Ya G.Communication Network Technology［J］，2012.

［4］Heider F.The Psychology of Interpersonal Relations［M］.Psychology Press，2013.

［5］Singhal A，Rogers E M.Entertainment-Education：A Communication Strategy for Social Change［M］.Routledge，2012.

［6］Wang X F，Li X，Chen G R.Complex Network Theory and Application［J］.Tsinghua University licensing Agency，2006.

Application of the Complex Network in Traditional Industry

ZHOU Qi-ming1，LIU Xiao-yuan2
（1.Chinese People's Liberation Army 92823 Forces，Sanya 572021；2.Luoding Polytechnic，Luoding 527200）

With the rise and development of complex network in recent years，more and more researchers have begun to use it to solve problems in other fields，such as life science and engineering.Thus，complex network theory is gradually penetrated into many different disciplines，and also many traditional industries are trying to apply complex network theory into practical problems.Introduces the research history and basic theory of complex network，then takes the research of interpersonal relationship and communication strategy as an example，builds the application model of complex network in tradition industry，and provides the common approaches for these problems.

Complex Network；Traditional Industry；Interpersonal Relationship；Communication Strategy

1007-1423（2016）21-0025-04

10.3969/j.issn.1007-1423.2016.21.005

周其明（1979-），男，本科，工程師，研究方向為計算機網絡技術

2016-04-27

2016-05-17

劉小園（1978-），男，碩士，副教授，研究方向為網絡數據庫系統