某型大口徑機槍地面適應性分析

范智滕，王瑞林，李永建

(1.西北核技術研究所，陜西 西安　710024；2.軍械工程學院，河北 石家莊　050003)

?

某型大口徑機槍地面適應性分析

范智滕1，2，王瑞林2，李永建2

(1.西北核技術研究所，陜西 西安710024；2.軍械工程學院，河北 石家莊050003)

為研究某型大口徑機槍的地面適應性，在分析了該槍架剛度的基礎上，以該機槍為研究對象，不考慮槍架的彈性變形，分析不同地面與駐鋤間的相互作用，建立了機槍在不同地面射擊時的穩定性理論模型。通過計算，結果表明該機槍有很好的地面適應性。對不同的駐鋤結構進行分析，提出了勤務使用方面的指導意見，發現了機槍采用不同駐鋤結構射擊時穩定性不同的本質，并依此提出了駐鋤結構優化方案。通過理論建模與對比分析，在一定程度上說明了優化方案的可行性。

大口徑機槍；地面適應性；駐鋤；穩定性；理論模型

某型大口徑機槍的作戰區域主要位于海拔較高的高原山地，嚴酷的作戰環境要求該機槍必須適合山地復雜環境架設，并在多種地面環境下都有良好的射擊精度。在該機槍的設計過程中為減輕質量提高機動性，在槍身尤其是槍架的設計上采用了大量新材料和新工藝，但是，武器系統質量的減小不可避免地會帶來射擊精度的降低。因此，必須對其地面適應性進行充分的論證研究。

根據以上背景，筆者從機槍在不同地面上射擊時的穩定性理論模型入手，對該機槍的射擊穩定性進行計算和分析，得出了相關結論并在此基礎上進行了駐鋤的結構優化。

1　槍架剛度的計算

所謂槍架的剛度，是指作用于槍架端點的外載荷與所產生的位移的比值，用剛度系數C來表示。槍架所受的主動力主要是槍身后坐階段的作用力，槍架的變形主要體現在后架桿部分，因左后架桿和右后架桿在結構上是對稱的，計算時可先計算單個后架桿的剛度，并計算在最大后坐推力作用下的槍架變形。

1.1槍架剛度計算模型

槍架剛度的計算模型如圖1所示。圖中x1表示AB架桿(托架)變形引起的位移；x2表示BC架桿(后架桿)變形引起的位移；J1、J2分別為托架、后架桿的截面慣性矩；l1、l2分別為托架、后架桿的長度。

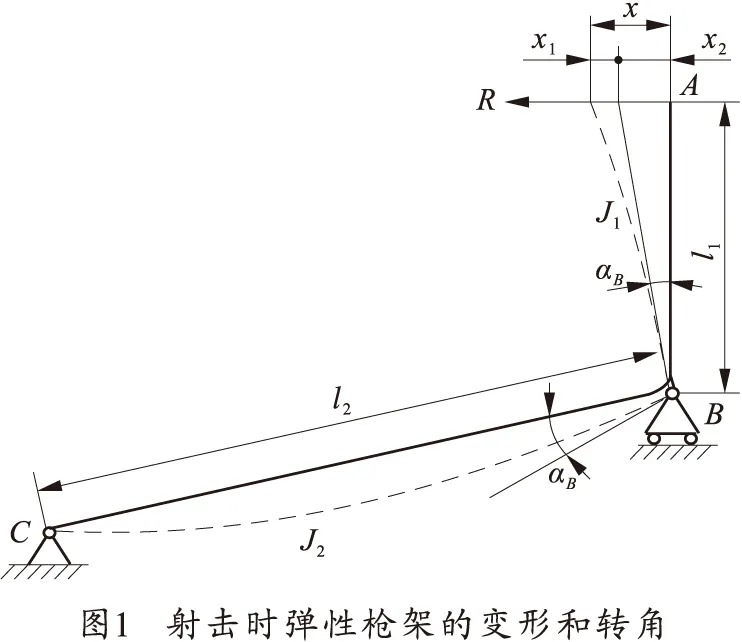
后架桿剛度C1的計算公式為

由材料力學知

式中：E1、E2分別為托架、后架桿的彈性模量；R1為槍架所受后坐推力沿單個后架桿方向上的分力。

一般情況下，托架的剛度比較大，抗彎剛度E1J1相比E2J2大得多，可略去其彈性變形的影響，根據上述公式可求出后架桿的剛度為

(1)

因該機槍后架桿的截面為矩形，其截面慣性矩為

式中：B為架桿截面外表面的寬度；H為架桿截面外表面的長度；b為架桿截面內表面的寬度；h為架桿截面內表面的長度。

1.2計算結果及分析

相同的槍架剛度對不同機槍的作用效果是不同的，這在一定程度上取決于機槍傳遞給槍架的作用力，為研究該機槍槍架的作用效果，用槍架受最大后坐推力下所產生的位移作為衡量指標，對槍架剛度的影響進行評估。

該型大口徑機槍三腳架的簡圖如圖2所示，該機槍的槍架為一支點在前，兩支點在后的結構形式，兩后架桿間的夾角為φ。

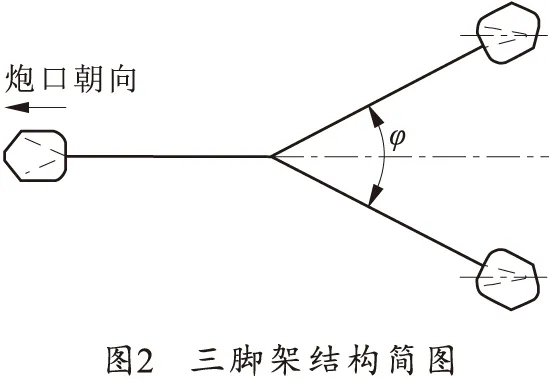
針對該結構，作用于單個后架桿上的力F1為

(2)

后坐推力R在機槍鉛垂面上引起A點的位移為

(3)

該型大口徑機槍的外機匣與三腳架剛性固連，在計算槍架所受的后坐推力時可等同為槍架的一部分。內、外機匣間由浮動簧和浮動體后緩沖簧連接，由于射擊過程中內機匣在外機匣上運動時前后均不發生剛性碰撞，所以槍架所受的最大后坐推力為浮動簧、浮動體后緩沖簧壓縮最大時的彈簧力和浮動體對外機匣的滑動摩擦力之和。

滑動摩擦力為

Fhd=ffdQfd

式中：ffd為浮動體與外機匣間的滑動摩擦系數；Qfd為浮動體的質量。

根據設計圖紙參數，浮動簧的極限工作長度為H3=95mm，浮動體后緩沖簧的極限工作長度為H2=104mm，則后坐力最大值對應浮動簧的長度為95mm，浮動體后緩沖簧的長度為104mm，各彈簧的剛度系數如表1所示。

表1　彈簧參數

則各彈簧力分別為

浮動簧力

F1=k1(H0-H3)

浮動體后緩沖簧力

F2=k2(H0-H2)

則槍架受到的最大后坐推力為

Rmax=Fhd+F1+F2

另外，計算機槍位移的初始參數為：E=110kN/mm2， B=31.4mm， H=37.15mm， h=35.75mm，l1=160mm，l2=750mm，φ=27°。可得

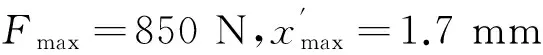
將計算所得數據與89式重機槍的最大后坐力4 560.0N[1]進行對比，發現該型大口徑機槍的后坐力得到了大大減小，并且該機槍在最大后坐推力作用下在鉛垂面上引起的位移值很小。因此，在該槍射擊穩定性建模分析中，可以不考慮槍架的彈性變形，視槍架為剛性結構。

2　穩定性理論計算

該型大口徑機槍的槍身運動部分與外機匣通過彈簧連接，外機匣與槍架固定連接，因此可將外機匣視為槍架的一部分，并將槍架按緩沖槍架來計算。

2.1基本假設

為了建立機槍穩定性模型，并在一定程度上簡化計算，提出以下基本假設[2]：

1)槍架在水平地面上平射。

2)不考慮槍架的彈性變形，視為剛性。

3)發射時所有作用在機槍上的力或其合力皆位于垂直對稱面內。

4)射擊時，機槍各支點不下沉。

2.2理論模型

由于槍架與槍身運動部分間存在相對運動關系，在分析槍架的受力前，必須首先研究機槍運動部分的受力及緩沖運動規律，受力分析如圖3所示。圖中Ft為膛底壓力；Fh為緩沖簧的抗力；Fm為內機匣與外機匣間的摩擦力；Qs為槍身運動部分的重力；e為槍身運動部分質心到槍膛軸線的距離。

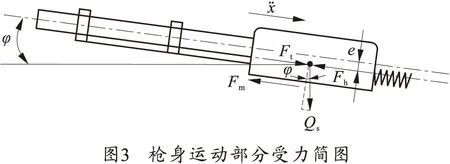
可列出槍身運動部分的運動微分方程為

(4)

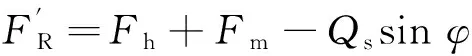
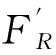
根據上述假設和槍身運動部分受力分析，射擊時槍身運動部分對槍架的作用有力FR和力矩Mt。不考慮抵肩力時的穩定性模型如圖4所示。圖中FTA、FTB為地面對前、后支點的水平作用力；FNA、FNB為地面對前、后支點的垂直作用力；W為全槍的重力；D為全槍質心到后支點的距離；L為前后支點之間的距離；ft為地面介質與垂直駐鋤面間的靜摩擦系數；ftFTA為地面介質對前支點垂直駐鋤面產生的靜摩擦力；hR為后支點到運動部分質心的距離。

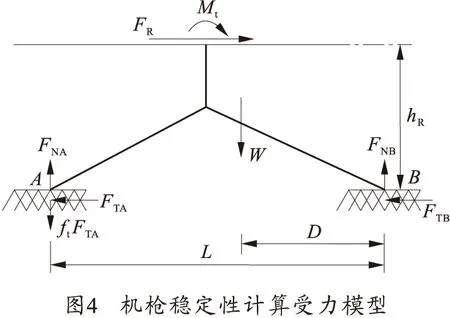
需要說明的是，力FNA、ftFTA不可能同時存在，只有當FNA=0，前支點具有上跳運動的趨勢時，ftFTA才存在并起穩定力矩的作用[2]。

列平衡方程為

其中,Mt=Fte。

在后坐過程中，以槍架前支點不離開地面作為穩定條件，即FNA≥0，可獲得穩定條件式。

當FNA>0時，ftFTA=0，由平衡方程可得穩定條件式為

WD≥FRhR+Mt

當FNA=0時，ftFTA>0，可得穩定條件式為

WD+ftFTAL≥FRhR+Mt

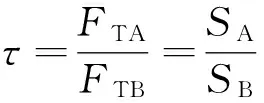
其中SA、SB分別為前后交點垂直駐鋤板與土壤的有效接觸面積。

則FNA=0時的穩定條件式變為

(5)

式(5)即為臨界狀態下的穩定條件式，不等式左側為穩定力矩MW，右側為翻倒力矩MF。

3　地面適應性分析

3.1粘土地面

某型大口徑機槍的前后駐鋤均為釬入式駐鋤，如圖5所示，并且從圖2可以看出駐鋤V形筋板的開口都朝向槍口方向。在粘土地面，駐鋤插入土壤，兩個斜面都與土壤相互接觸，既能提供土壤抗力，又有一定的導向作用。機槍射擊過程中駐鋤水平滑動產生的摩擦力相對土壤抗力非常小，可忽略。因此，粘土地面的穩定性模型即是圖4所示的模型。

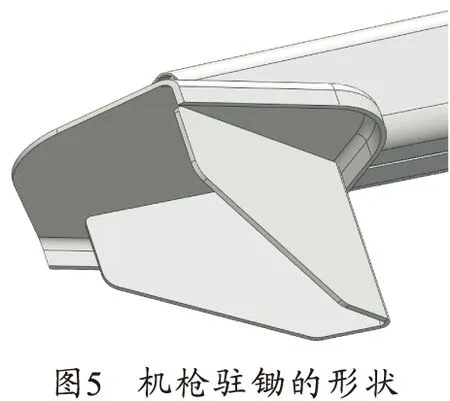
穩定條件式為式(5)。

(6)

3.2水泥地面

機槍在水泥地面射擊時，槍身可以同槍架一起向后滑動，地面只提供滑動摩擦系數，不考慮抵肩力時的穩定性模型如圖6所示，hC表示機槍質心到后支點的距離。

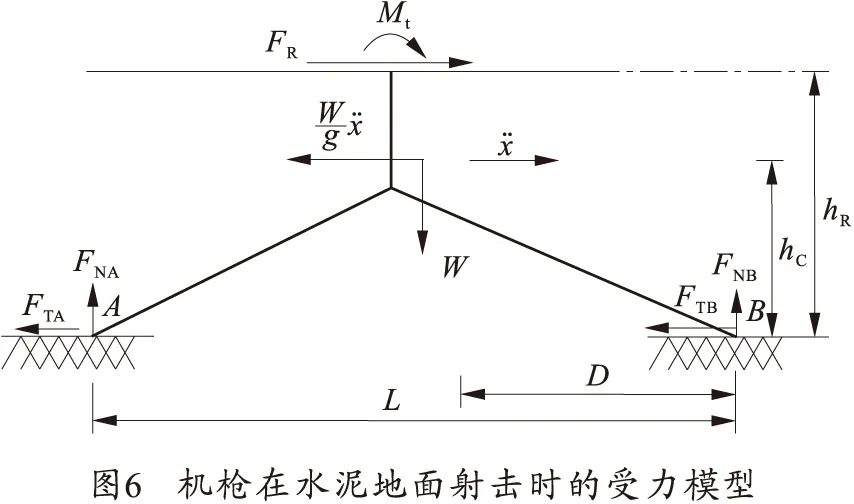
應用達朗伯原理，列出平衡方程，并同樣可得到不考慮抵肩力F時的穩定條件式為

(7)

當考慮抵肩力F時，穩定條件式為

(8)

3.3計算結果及分析

在實際的射擊過程中，機槍后坐階段翻倒力矩只可能出現兩次極大值，最大膛壓瞬間和后坐到位瞬間。最大膛壓瞬間：Ft1=40kN，FR1=100N；后坐到位瞬間：Ft2=0，FR2=850N。

另外，穩定性計算時的初始數據如下：

W=225.4N，D=0.625m，L=1.304m，hR=0.27m，hC=0.24m，e=0.009m，Qs=110.17N，SA=4 264.90mm2，SB=4 739.88mm2粘土地面：f=0.66，ft=0.85；水泥地面：f=0.6，ft=0.8。

在實際射擊過程中，槍架和土壤產生變形以及槍架的后坐運動需要吸收一部分后坐能量，在機槍的穩定性分析中常常引入能量損失修正系數μ。根據實踐經驗，能量損失修正系數μ常取1/3～1/4[3]。考慮本模型土壤變形及槍架變形的特點，可取μ為1/3。可以得到2種地面下的穩定性計算結果如表2所示，其中后坐到位時刻沒有考慮抵肩力的作用。

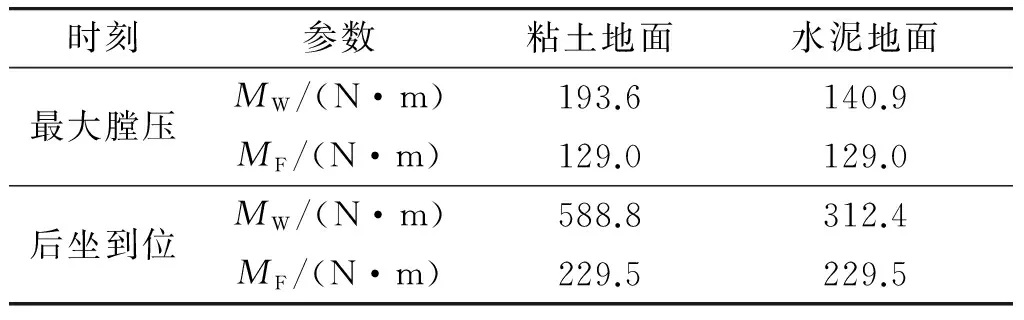
表2　2種地面下的穩定性計算結果

分析表格中數據可以得出以下結論：

1)該機槍插入粘土地面甚至直接放在水泥地面上射擊時都可以達到射擊穩定，說明該機槍對地面環境不敏感，可以多種地面。對比最大膛壓和后坐到位時刻的穩定力矩值，可知在粘土地面上射擊時穩定性更好。

2)在最大膛壓時刻，粘土地面的穩定力矩大于水泥地面，是因為在粘土地面射擊時，駐鋤可插入土壤，有附加穩定力矩ftFTAL的作用，所以在粘土地面穩定性更好。

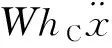
4)對比該槍在最大膛壓和后坐到位時刻的穩定性數據可知，在2種地面上射擊時，最大膛壓瞬間都是相對較為危險的時刻。2種地面穩定性模型中翻倒力矩表達式都為MF=FRhR+Mt，則在最大膛壓瞬間，Mt對翻倒力矩起主要作用。因此，可以通過減小槍身運動部分質心到槍膛軸線的距離e來減小翻倒力矩，使機槍射擊更加穩定。

4　駐鋤結構優化

三腳架式武器的駐鋤可分為釬入式和滑動式駐鋤兩種形式，如圖7所示[4]。

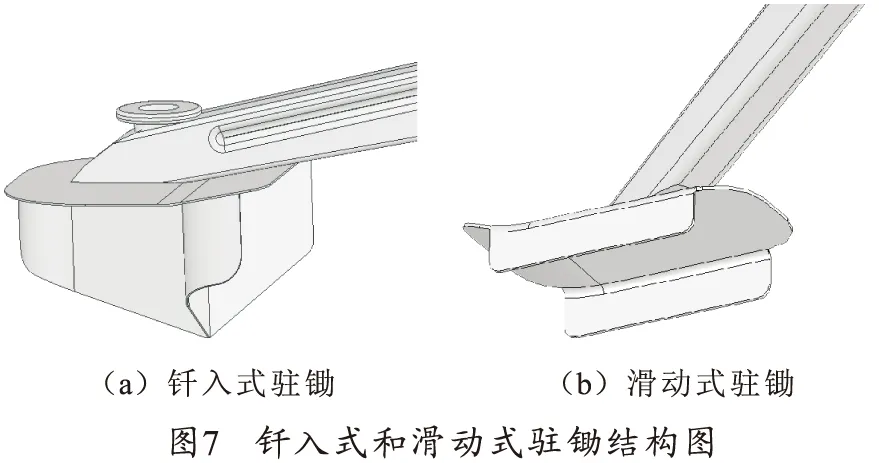
當使用釬入式駐鋤插入土壤進行射擊時，機槍固定不動，土壤可為前、后駐鋤提供向前、向上的抗力，并為前駐鋤提供向下的靜摩擦力，使射擊更加穩定，穩定性計算模型如圖4所示。當使用滑動式駐鋤射擊時，機槍可以前后滑動，無論駐鋤插入土壤還是僅放置在地面上，地面介質對駐鋤的作用力主要為向上的抗力和與移動方向相反的摩擦力，穩定性計算模型如圖6所示。

如果將前駐鋤設計成釬入式、后駐鋤設計成滑動式，射擊穩定性是不是會更好呢？下面通過模型來分析這個問題。這種槍架的結構可用于除水泥地以外的各種地面介質中，是具有很好的適應性的。

不考慮抵肩力，穩定性模型如圖8所示。

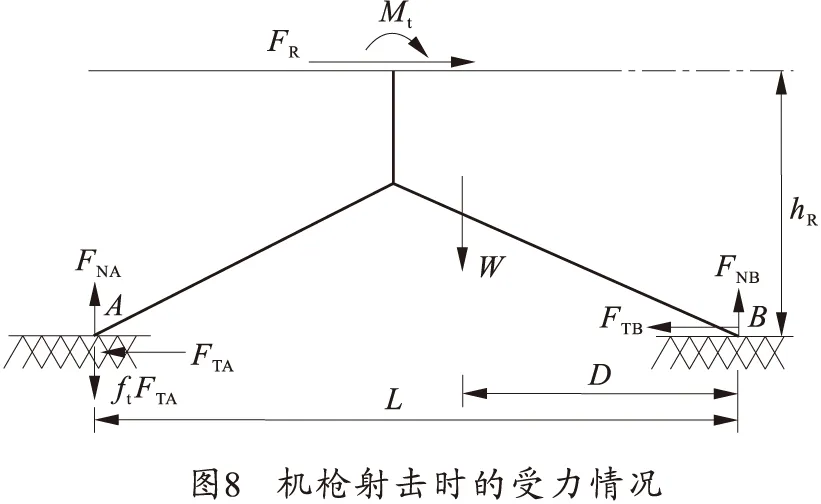
同樣可以得出臨界狀態FNA=0時的穩定條件式為

WD+ftFTAL≥FRhR+Mt

(9)

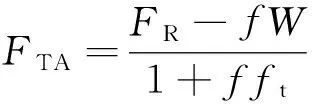
利用前文的初始數據可計算機槍用該駐鋤形式射擊時的穩定性。

機槍采用釬入式駐鋤和滑動式駐鋤在粘土地面射擊時的穩定性計算模型分別與前文某型大口徑機槍在2種地面介質上的射擊穩定性計算模型相對應，只是將圖6中的地面介質改為粘土。機槍采用3種駐鋤形式在水泥地面射擊時的穩定性計算模型都為圖6所示模型，計算結果如表2中水泥地面所示。機槍采用3種駐鋤形式在粘土地面射擊時的穩定性計算結果，如表3所示。

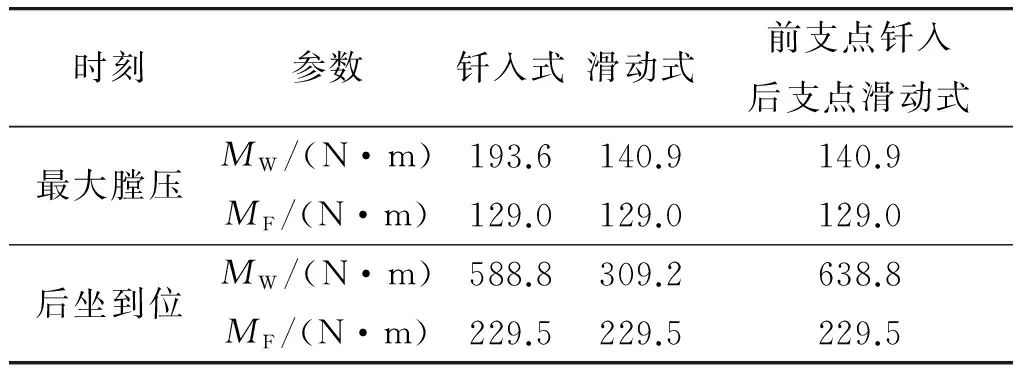
表3　3種駐鋤形式的穩定性計算結果

經分析，可以得出以下結論：

1)某型大口徑機槍因后坐力小，駐鋤的形狀對機槍的穩定性影響不是很大，采用3種駐鋤都可以滿足穩定性要求。

2)釬入式駐鋤結構更適合松軟的土壤。駐鋤插入土壤中，土壤提供的抗力及彈性變形吸收后坐能量的作用，不僅可以使射擊更加穩定，提高射擊精度，還可以減小武器后坐力對射手的影響。

3)滑動式駐鋤結構更適合硬質地面。射擊過程中不需要將駐鋤插入地面中，只要駐鋤能有效地滑動，在射手的抵肩作用下機槍就可以達到射擊穩定。

4)機槍采用釬入式駐鋤在粘土地面射擊時，只需要將前駐鋤插入土壤，后駐鋤在地面上水平放置，就可以滿足射擊穩定性。此時的模型與前支點釬入后支點滑動式駐鋤穩定性模型相同。采用此種架設方式在勤務使用上更為方便。

比較幾個穩定條件式可以發現，除附加穩定力矩項外，其余項都是相同的，說明2種駐鋤結構形式的本質區別就在于附加穩定力矩的大小。因此，可將2種駐鋤的優勢集中，讓2個附加穩定力矩在一種駐鋤結構上得以實現，即優化后的駐鋤結構既可以前后滑動，又可以在上跳時受土壤靜摩擦力的作用。

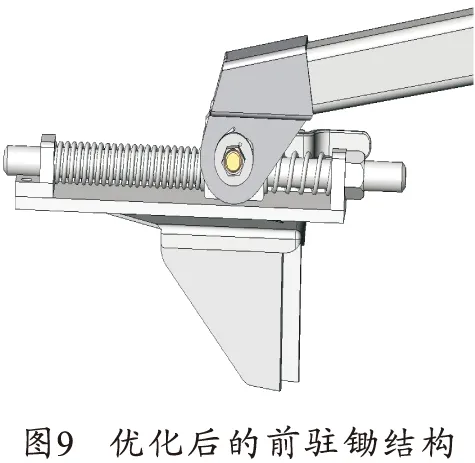
優化后的前駐鋤結構如圖9所示，即緩沖駐鋤，它利用導柱和彈簧實現前后滑動和緩沖，駐鋤板為V形，可插入土壤中。相關結構設計和參數優化已有文獻作出研究[5-6]。后駐鋤采用滑動式駐鋤結構。

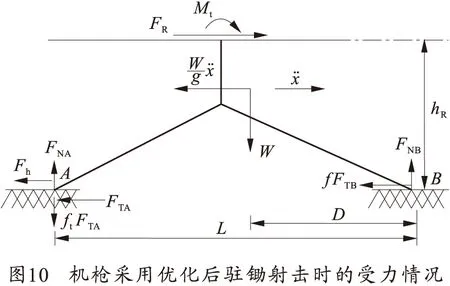
機槍采用優化后駐鋤結構在粘土地面射擊時的穩定性模型如圖10所示。Fh為前駐鋤的緩沖簧力。

可以得出的穩定條件式為

(10)

對比式(7)、(9)、(10)發現，式(10)的附加穩定力矩為前2種的附加穩定力矩之和，可知優化后的駐鋤結構綜合了釬入式和滑動式駐鋤的優點，使附加穩定力矩更大，機槍的射擊穩定性得到了更好的保證。

5　結論

筆者以某型大口徑機槍為研究對象，通過對機槍在不同地面的建模與結果分析，挖掘出了機槍在不同地面上射擊穩定性不同的本質，確定了影響機槍射擊穩定性的危險時刻，依此對機槍的實際射擊使用提出了指導意見，并針對性地提出了增強穩定性的措施。以地面適應性分析的計算模型為基礎，對比分析了不同駐鋤結構方案對不同地面的適應性，依此提出了駐鋤結構的優化方案，通過建模分析與對比，在一定程度上說明了駐鋤優化方案的可行性。

通過分析可知，雖然某型大口徑機槍質量得到了減小，但因武器后坐力的減小，降低了射擊振動，提高了武器射擊精度，使之能夠適應高海拔下不同的地面環境。該機槍的穩定性論證及結論分析方法為大口徑機槍的穩定性論證及改進設計打下了良好的基礎。

References)

[1]董應超. 某三腳架座的大口徑機槍動力學仿真與關鍵技術研究[D]. 南京：南京理工大學,2011.

DONG Yingchao. Structure dynamics simulation and key technology of a machine gun with tripod mount[D]. Nanjing:Nanjing University of Science and Technology, 2011. (in Chinese)

[2]王瑞林,陳運生,郝躍偉. 機槍相對穩定性理論及模型研究[J]. 南京理工大學學報,2004,28(5): 472-475.

WANG Ruilin,CHEN Yunsheng,HAO Yuewei.Relative stability theory and model for machine gun[J]. Journal of Nanjing University of Science and Technology,2004,28(5): 472-475. (in Chinese)

[3]步兵自動武器及彈藥設計手冊編寫組. 步兵自動武器及彈藥設計手冊(中冊)[M].北京：國防工業出版社,1977: 582-586.

InfantryAutomaticWeaponsandAmmunitionDesignManualEditorial Committee. Infantry automatic weapons and ammunition design manual:the seconcl volume[M]. Beijing: National Defense Industry Press, 1977: 582-586. (in Chinese)

[4] 李永建. 某型機槍結構動力學仿真與參數優化[D]. 石家莊：軍械工程學院,2007.

LI Yongjian.Structure dynamics simulation and parameter optimization of a type of machine gun[D]. Shijiazhuang:Ordnance Engineering College, 2007. (in Chinese)

[5]王瑞林,李永建,張軍挪. 駐鋤緩沖式槍架設計[J]. 兵工學報,2007,28(2): 144-147.

WANG Ruilin, LI Yongjian, ZHANG Junnuo. Design of a machine gun mount with buffer-type spade[J]. Acta Armamentarii,2007,28(2): 144-147. (in Chinese)

[6]張軍挪,尚利民,李永建,等. 緩沖駐鋤槍架的結構設計及參數優化研究[J]. 中北大學學報:自然科學版,2011,32(3): 276-279.

ZHANG Junnuo, SHANG Limin, LI Yongjian,et al. Research on structural design and parameter optimization of machine gun mount with buffer-type spade[J]. Journal of North University of China:Natural Science Edition, 2011,32(3): 276-279. (in Chinese)

Ground Adaptability Analysis of a Large Calibre Machine Gun

FAN Zhiteng1,2, WANG Ruilin2, LI Yongjian2

(1.Northwest Institute of Nuclear Technology, Xi’an710024, Shaanxi, China;2.Ordnance Engineering College, Shijiazhuang050003, Hebei, China)

To study the ground adaptability of a certain type of large calibre machine gun, its stability theory model firing at different ground was established. In this model, the machine gun was chosen as the study object, the stiffness of rifle rack was analyzed, the elasticity deformation of rifle rack was not considered, and the interaction between different ground and spade was analyzed reasonable. The results show that the gun has good ground adaptability. Based on this, analyzing different spade structure, guidance on the use of this gun was proposed. The stability difference essence of machine gun firing on use of different spade was discovered. On this basis, the spade optimization program was put forward. Through theoretical modeling and comparative analysis, the feasibility of the optimization program was proved to some extent.

large calibre machine gun; ground adaptability; spade; stability; theory model

2014-11-18

范智滕(1990-)，男，碩士，主要從事武器系統動力學理論與應用研究。E-mail：zhitengfan@163.com

TJ25

A

1673-6524(2016)01-0021-06