Ridge-type spectral decomposition estimators inmixed effects models with stochastic restrictions

ZHENG Lu, YUE Rongxian, CHENG Jing

(1.College of Mathematics and Science,Shanghai Normal University,Shanghai 200234,China;2.College of Science,Anhui Agricultural University,Hefei 230036,China)

?

Ridge-type spectral decomposition estimators inmixed effects models with stochastic restrictions

ZHENG Lu1, YUE Rongxian1, CHENG Jing2

(1.College of Mathematics and Science,Shanghai Normal University,Shanghai 200234,China;2.College of Science,Anhui Agricultural University,Hefei 230036,China)

This paper proposes a new estimation of fixed effects in linear mixed models with stochastic restrictions,which is called a conditional ridge-type spectral decomposition estimator.Using the mean squared error matrix and generalized mean squared error as criteria for comparing the estimates,we establish sufficient conditions for the superiority of the conditional ridge-type spectral decomposition estimator over the conditional spectral decomposition estimator.The upper and lower bounds of the relative efficiency are also given.Finally,a simulation example is given to illustrate the theoretical results.

linear mixed mode; mean squared error matrix; ridge-type spectral decomposition estimatior; stochastic linear restrictions

1　Introduction

Linear mixed model is an important statistical model.In the recent twenty years,linear mixed models have found more and more applications in the fields of biology,medicine,economy,finance,environment science,sample investigation and mechanical engineering[1-5].Based on spectral decomposition,a further study of estimation about fixed effect is made in this paper.Spectral decomposition (SD) estimation was proposed by Wang and Yin[6].With this method we can obtain several SD estimators,which are all unbiased estimators.

Consider the following general linear mixed model

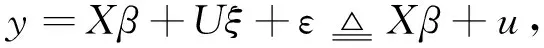
(1)

whereyis ann×1 vector of observations,Xis ann×pknown design matrix with full column rank,βis anp×1 vector of fixed effect,Uis ann×pdesign matrix,ξis anq×1 vector of random effect,εis ann×1 vector of random disturbances.Suppose that

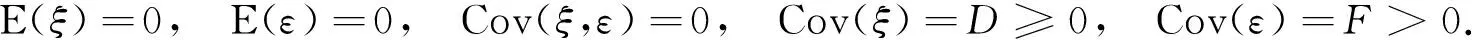
It follows that

V=Cov(y)=Cov(u)=UDUT+F≥0.

By spectral decomposition on the covariance matrix,we have

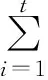
We multiplyPifrom the left on both sides of (1),and denote

y(i)=Piy, Xi=PiX,ui=Piu.

Then we have the following transformed model:

(2)

It is easy to obtain that E(ui)=0 and Cov(ui)=λiPi.Note thatPiis a singular matrix,and then model (2) is a singular linear model.

Wang and Yin[6]proposed spectral decomposition estimation (SDE) to estimate the fixed effectsβand the variance components simultaneously.A prominent feature of this method is that for the fixed effects we can obtain several spectral decomposition estimates.Specifically,for every eigenvaluesλi,the spectral decomposition estimators of its corresponding fixed effectsβare given by

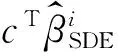
wherer=rk(Pi)-rk(Xi).

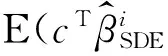
(3)

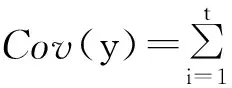
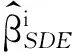
(4)

whereki>0andQiistheeigenvectormatrixofXTPiX.Thepartialridge-typespectraldecompositionestimatorissuperiortothespectraldecompositionestimatorinthesenseofmeansquarederrormatrix.

Thispaperbeginswithanintroductorysectioncontainingabriefreviewoftheestimatorsonfixedeffects.Itisworthnotingthat,theaboveestimatorsareobtainedbyestimatingtheregressioncoefficientsβfromthelinearmixedmodelitself.Whereasintheregressionmodelfordescribingeconomicphenomena,inadditiontothesampleinformation,wetendtogetsomepriorinformation.Withthesepriorinformation,theregressioncoefficientestimateshavemoresuperiorpropertiesthanthosehavenopriorinformation.Thefundamentalpurposeofthispaperistointroduceanewconditionalridge-typespectraldecompositionestimator(CRSDE)forthefixedeffects.

Therestofthispaperisorganizedasfollows.Section2introducestheconditionalspectraldecompositionestimator(CSDE),andSection3introducestheCRSDE.ThesetwoestimatorsarecomparedinSection4.AnumericalexampleisgiventoillustratesomeofthetheoreticalresultsinSection5andsomeconclusionremarksaregiveninSection6.

2　Conditional spectral decomposition estimate

Considerthelinearmixedmodel(1)withrespecttothefollowingstochasticrestriction:

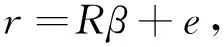
(5)

whererisaj×1knownrandomvector,Risagivenj×pmatrixwithfullrowrank,eisaj×1vectorofrandomdisturbanceswithmean0andcovariancematrixWwhichisaknownpositivematrix.Supposethatuandeareuncorrelated.

Merge(2)with(5)asfollows:

(6)

Wedenote

andrewrite(6)as

(7)

Notethat

Because(2)isasingularlinearmodel,sothemodel(7)isasingularlinearmodelwithstochasticlinearrestrictions[9].

WedefinetheCSDEofβtobethefollowing:

(8)

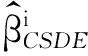
Letδi1≥δi2≥…≥δiri>0bethepositiveeigenvaluesof(XTPiX+λiRTW-1R) , ri≤p ,andφi1,φi2,…,φiribethecorrespondingstandardizedeigenvectors.DefineΦi=(φi1,φi2,…,φiri).Wethenhave

and

Therefore,wecaneasilygetthemeansquarederror(MSE)oftheCSDE:

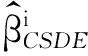
3　Conditional ridge-type spectral decomposition estimate

Definethefollowingestimatorsofthefixedeffectsβinthemixedmodel(7):

(9)

ThesearecalledtheCRSDE.Notethat

andthen

Therefore,theCRSDEsin(9)areStein-typebiasedestimators.

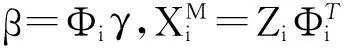
(10)

TheCSDEofγin(10)isgivenby

(11)

andtheCRSDEofγisgivenby

(12)

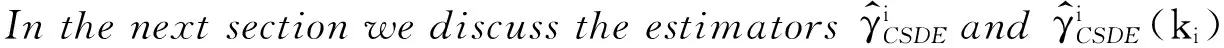
4　Superiority of the conditional ridge-type spectral decomposition estimator

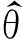
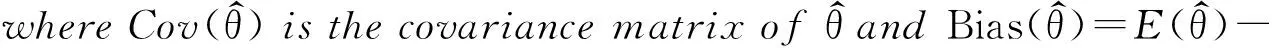
whereDisapositivedefinitematrix.ThefollowingtwolemmasareusefulforcomparingtheMSEMandGMSEofestimators.

Lemma 4.1[10,Theorem A.71]LetAbe ann×nsymmetric matrix,xbe ann-vector,andα>0 be any scalar.Then the following statements are equivalent:

(i)αA-xxT≥0.

(ii)A≥0,x∈R(A),andxTA-x≤α,withA-beinganyg-inverseofA,whereR(A)isthevectorspacespannedbythecolumnvectorsofA.

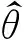
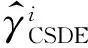
(13)

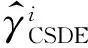
(14)

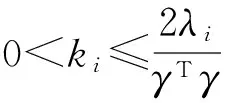
Therefore,we have

and the proof is completed.

Theorem 4.2For model (7) within the ellipsoidγTΛiγ≤λifor eachi∈{1,…,t},we have

(15)

where

ProofFrom (13) and (14),we conclude that

Denote

We then have

and then the desired result (15) follows from Lemma 4.2.

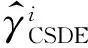
Theorem 4.3The relative efficiency satisfies

ProofAccording to the definition of the relative efficiency,we have

Becauseδi1≥δi2≥…≥δiri>0 and

it follows that

The proof is completed.

5　Monte-carlo simulation study

To illustrate our theoretical results,we now consider a simulation study to compare the performance of the estimators introduced in previous sections.This study was discussed by Gumedze and Dunne[11]and Yang,Ye and Xue[12].Here the linear mixed model is given by

wherei=1,…,5,j=1,…,10 withβ=(β1,β2,β3)T=(2,1.5,2)T,and theξare iid random effects with distributionN(0,0.5) ,andeijare iid random disturbances with distributionN(0,1).The explanatory variablesx1ij,x2ijandx3ijare generated pseudo-numbers from uniform distributionsU(1,3),U(2,4) andU(0,1),respectively.The covariance matrix ofξi+eijis given by

The distinct eigenvalues ofVareλ1=6 andλ2=1.

Assume that the following stochastic linear restrictions are used:

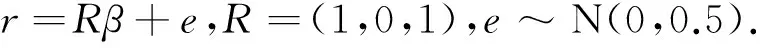
In the simulation study,J=1000 replicates are generated andthe estimated mean squared errors (EMSE) for estimators are calculated as

where the subscriptjrepresents the estimators in thejth repeated experiment.Then using the equations in (3),(8) and (9) corresponding toλ2,we compute the EMSE values of the SDE,CSDE and CRSDE by the above formulas.The simulation results are shown in Table 1.

Table 1　EMSEs of SDE,CSDE and CRSDE (i=2) for β=(β1,β2,β3)T

We observe that the CRSDE and CSDE forβare superior to the SDE.And when ridge parameterkis small enough,the CRSDE is superior to the CSDE.The Monte Carlo simulations agree with our theoretical discovery in this paper.We can conclude that the CRSDE is meaningful in practice.

6　Conclusion

In this paper,the CSDE and CRSDE for the parameters of fixed effects in a linear mixed model are proposed when the prior information is available about the parameters.Furthermore,we show that the CRSDE is superior to the CSDE and SDE in the sense of MSEM under certain conditions.The upper and lower bounds of the relative efficiency are also given.Finally,we illustrate our results with a Monte-Carlo simulation study.

References:

[1]Verbeke G,Molenberghs G.Linear mixed models in practice:a SAS-oriented approach.Lecture Notes in Statistics 126 [M].New York:Springer-Verlag,1997.

[2]Verbeke G,Molenberghs G.Linear mixed models for longitudinal data [M].New York:Springer-Verlag,2000.

[3]Wang S G,Chow S C.Advanced linear models [M].New York:Marcel Dekker Inc,1994.

[4]Khunri A I,Mathew T,Sinha B K.Statistical tests for mixed linear models [M].New York:John Wiley,1998.

[5]Searle S R,Casella G,McCulloch C E.Variance components [M].New York:John Wiley,1992.

[6]Wang S G,Yin S J.A new estimate of the parameters in linear mixed models [J].Science in China (Series A),2002,32(5):434-443.

[7]Rao C R,Toutenburg H.Linear models:Least squares and alternatives [M].New York:Springer-Verlag,1995.

[8]Yang H,Li Y L.Partial ridge-type spectral decomposition estimator in linear mixed model (in Chinese) [J].Chinese Journal of Applied Probability,2008,24(3):289-296.

[9]Xu J W,Yang H.Estimation in singular linear models with stochastic linear restrictions [J].Communications in Statistics-Theory and Methods,2007,40(24):4364-4371.

[10]Rao C R,Toutenburg H,Heumann S C.Linear models and generalizations:least squares and alternatives [M].New York:Springer-Verlag,2008.

[11]Gumedze F N,Dunne T T.Parameter estimation and inference in the linear mixed model [J].Linear Algebra and its Applications,2011,435(8):1920-1944.

[12]Yang H,Ye H L,Xue Kai.A further study of predictions in linear mixed models [J].Communications in Statistics-Theory and Methods,2014,43(20):4241-4252.

(責(zé)任編輯:馮珍珍)

10.3969/J.ISSN.1000-5137.2016.04.001

具有隨機(jī)約束的混合效應(yīng)模型參數(shù)的嶺型譜分解估計(jì)

鄭鷺1, 岳榮先1, 程靖2

(1.上海師范大學(xué) 數(shù)理學(xué)院,上海 200234; 2.安徽農(nóng)業(yè)大學(xué) 理學(xué)院,合肥 230036)

對于具有隨機(jī)線性約束的線性混合效應(yīng)模型參數(shù)提出一種稱之為條件嶺型譜分解估計(jì)的方法.利用均方誤差矩陣和廣義均方誤差對固定效應(yīng)參數(shù)的幾種估計(jì)量進(jìn)行比較,給出條件嶺型譜分解估計(jì)優(yōu)于條件譜分解估計(jì)的充分條件,并給出這兩種估計(jì)的相對效率的上下界.最后,模擬算例驗(yàn)證了理論結(jié)果的正確性.

混合效應(yīng)模型; 均方誤差矩陣; 嶺型譜分解估計(jì); 隨機(jī)線性約束

date: 2016-03-20

Shanghai Municipal Science and Technology Research Project (14DZ1201900);NSFC grant (11471216);NSFC grant (11401056)

YUE Rongxian,College of Mathematics and Science,Shanghai Normal University,No.100 Guiling Rd,Shanghai 200234,China,E-mail:yue2@shnu.edu.cn

O 212.4Document code: AArticle ID: 1000-5137(2016)04-0387-08