以形助數探索運算規律

盧笙華

以形助數探索運算規律

盧笙華

“數學是思維的體操。”小學數學新課標中將課程目標由原來的“雙基”發展為“四基”，其中就增加了“基本數學思想”。數學思想很難教會，只能慢慢滲透，猶如春雨“潤物細無聲”，也只有厚積才能薄發。

數形結合是數學教學中常用的思想方法，它可以使某些抽象的數學問題直觀化、生動化，有助于把握數學問題的本質，使很多問題迎刃而解。

接著教師引導：解答這樣的題除了通分計算外，還有沒有什么規律呢？我們可以畫一個正方形表示“1”……（如圖1）。從圖中可以看出：。用同樣的方法可以得到：。

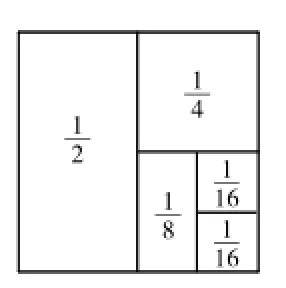
圖1

借助于具體的圖形，學生在直觀的圖形變化中更容易悟出其中的運算規律：如果前一個分數依次是后一個分數的2倍，求這樣一組分數的和，只要用第一個分數的2倍減去最后一個分數就可以得出結果。

此時教師引導：依據前面的做法，我們可以把每個分數在一個大圓中依次表示出來。（課件演示，逐漸形成圖2）

學生能夠直觀地發現：這些分數的和慢慢地接近整個圓，只少了最后一次平均分成兩份中的一份。當加到時，就比整個圓少了（如圖3）。所以

。

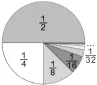
圖2

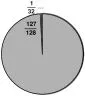
圖3

教師在數學教學中要善于發掘“數”與“形”的本質聯系，借助數形結合，把方法落到實處，讓學生逐步掌握數形結合的思想，并使之成為學習數學、運用數學和發展數學的工具。

（作者單位：浙江省義烏市香山小學）