古建結構中側腳和升起傳力機理
王建省 張 建 王雪梅
?
古建結構中側腳和升起傳力機理
王建省 張 建 王雪梅
目前已有的古建筑研究較少對于側腳和升起進行單獨的分析,文章從獨立的側腳、升起的角度進行結構影響方面的研究。以某元宮古建結構為分析基礎,進行簡化并對其進行結構建模,施加不同的荷載,分別計算有無側腳、升起時產生的位移和作用反力,計算了整體結構的不同位移,并對整體結構進行縱向比對。計算結果表明,側腳和升起在結構中作用非常明顯,尤其是對抵抗外力起到了關鍵作用。
“凡立柱,并令柱首(即柱頭)微收向內,柱腳(即柱根)微出向外,謂之側腳。”各柱側腳的數值的規定:“每屋正面隨柱之長,每一尺即側腳一分。若側面每長一尺即側腳八厘,至角柱,其柱首相向各依法本。”升起,即“當心間柱高不懂,次間,梢間,盡間柱頭相對當心間柱頭依次升高2寸,使檐口形成一條緩和的曲線”。目前,對于側腳的研究主要集中于其對于木結構抗震作用的影響以及對于工藝做法的結構意義的一些定性分析,而對于升起的研究,大多是評論其美觀性和裝飾性,而對于此兩者在外力作用下對于產生的位移和反力的影響的研究很少,所以本文重點要研究的是對其側腳及升起在受外荷載時對于結構的位移的影響以及二者對由于外力產生的柱子底端反力的影響,以此來分析側腳及升起對結構的作用。
此樓閣各層平面都是對稱布置,圖1為元宮的首層平面圖簡化圖,明間長度為7.2m,寬度6.1m,次間長度7.2m,寬度5.1m,布局規格簡單,且為對稱結構。
本文模型分析所用結構為某元宮的結構,按照原古建筑的結構形式,利用有限元進行仿古建模分析。
其中檐柱,金柱,檐枋,抱頭梁及五架梁等構件的尺寸形式如表1所示。

表1 構件尺寸表
建模過程
梁、柱、枋都選擇beam188單元模型。Beam188單元適合于分析從細長到中等粗短的梁結構,該單元基于鐵木辛哥梁結構理論,并考慮了剪切變形的影響。該單元是三維線性(2節點)或二次梁單元。每個節點上有6個或7個自由度。當KEYOPT(1)=0時,每個節點有6個自由度;節點坐標系的x、y、z方向的平動和繞x、y、z軸的轉動。所以該單元非常適合線性、大角度轉動和非線性大應變問題。將屋蓋的總質量簡化為集中荷載分別加在各柱的頂端,用mass21單元來模擬。mass21單元是1節點質量單元。每個節點上具有6個自由度:x,y,z方向的位移自由度和繞x,y,z軸的旋轉自由度。可以給該單元的每個方向施加不同的質量和轉動慣量。由于榫卯結構連接的復雜性,將榫頭和和卯口接觸面采用TARGE170單元和CONTA173單元模擬面接觸可以較為接近真實情況
屋蓋荷載計算
由于古建筑的屋面荷載無相關規范,借鑒于現今的規范對屋蓋自重進行計算,以滿足房屋安全性能的要求。屋蓋自重為1.8KN/m2。
根據《建筑結構荷載規范》(GB5009—2012)第6.1.1條,屋面雪荷載標準值按50年一遇雪壓采用,即0.4KN/ m2,組合系數采用0.7,屋面積雪分布系數取0.8。所以雪載標準值
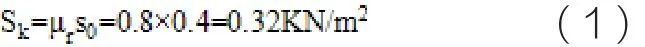
式中 SK—雪荷載標準值
μr—屋面積雪分布系數
S0—基本雪壓

圖1 某元宮建筑平面圖

圖2 結構模型圖

圖3 簡化鋼架結構
根據《建筑結構荷載規范》(GB5009—2012)第3.2.3條,荷載基本組合按下式取用:
由可變荷載效應控制的組合
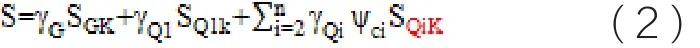
由永久荷載效應控制的組合
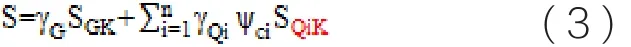
式中:γG—永久荷載分項系數,可變荷載控制時取1.2,永久荷載控制時取1.35。
γQi—第i 個可變荷載分項系數,取1.4。
SGK—永久荷載標準值產生的荷載效應。
SQiK—第i 個可變荷載產生的荷載效應。
ψci—可變荷載組合系數。
根據《建筑結構荷載規范》(GB5009—2001)第4.1.1條,屋面活載標準值為2.0KN/m2,組合系數為0.7,折減系數為1.0。
所以,當由可變荷載效應控制的組合時
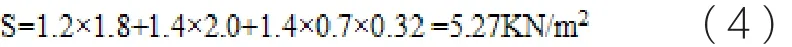
由永久荷載效應控制的組合時

所以屋蓋主體結構所承受荷載為5.27 KN/m2。
邊界條件假設
將原建筑結構簡化,柱根約束x、y、z方向的平動和繞x、y、z軸的轉動的自由度,建立模型如圖2所示。
對于古建筑一般都是框架結構。現就一簡單的結構運用力學理論行分析。
如圖3,是一個簡單的剛架結構,在結點3處施加一水平外力。
則對于結點4,其彎矩值為:

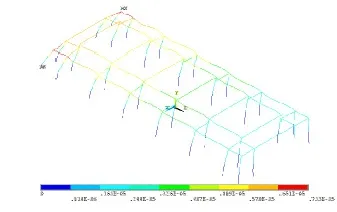
圖4 有側腳結構位移云圖
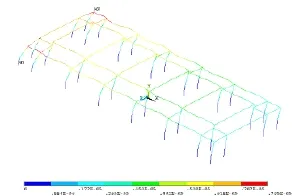
圖5 無側腳結構位移云圖

圖6 節點詳圖
經推導可得結點4的水平位移:
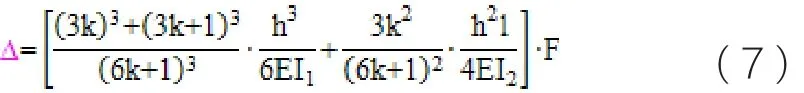
由以上結論可知,對于框架結構,其結點位移與外力成正比。所以本文利用模型柱頂的位移來體現外力分別對有側腳和升起結構的影響。
側腳對結構穩定性貢獻的分析
如圖4,圖5分別為結構在有無側腳情況時在外力作用下的位移云圖。
圖6為各節點具體位置。
為了能清晰地顯示模型結構隨著外力變化的趨勢,對比出有無側腳對外力的抵抗效果,選擇關鍵處節點,67節點及317 節點,并畫出結構頂端外力逐漸增大時,其位移的變化趨勢圖。如圖7,圖8所示。
結構有無側腳情況下整體各個節點位移的對比,如表2所示。
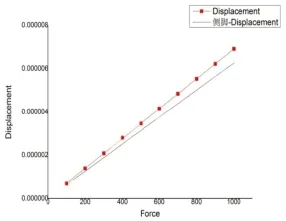
圖7 節點67外力-位移圖

圖8 節點317外力-位移圖
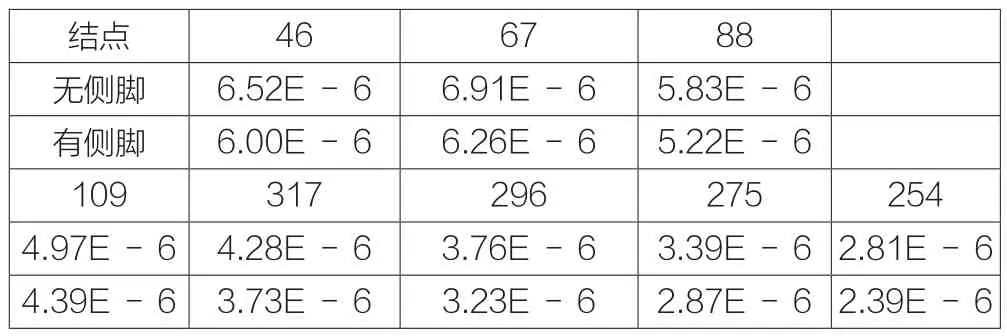
表2 各節點位移
分析關鍵結點有無側腳結構柱子底端的反力,如圖9,圖10所示。
根據上述有無側腳結構的分析數據對比,顯然有側腳結構的節點位移比無側腳結構的節點位移要小;同時,45節點對應柱底端和306節點對應柱底端的反力,在有側腳結構的柱端反力隨外力逐漸增大時,小于正常結構的柱底端反力,且二者之間的差值會逐漸增大。主要是因為檐柱設置側腳后, 將一部分豎向力分解為水平力, 致使檐柱軸壓力減小,在向下傳遞至柱底端的壓力也隨之減小,所以柱端反力會因為側腳的存在而減小。說明有側腳建筑能夠有效地抵抗外力對柱子頂端產生側移及底端產生反力的影響,從而提高建筑結構的整體性和穩定性。
升起對結構整體穩定性分析
如圖11,圖12分別為結構有無升起情況時在外力作用下的位移云圖。如圖13,圖14所示,為結點67及結點317的外力-位移圖。
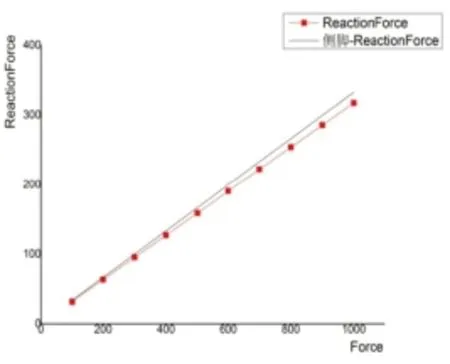
圖9 節點45 外力-反力圖
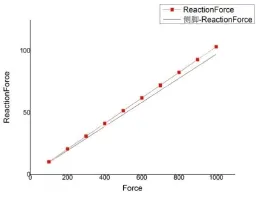
圖10 節點306外力-反力圖
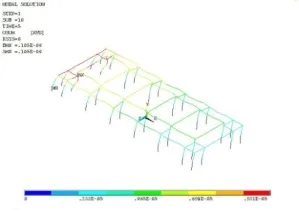
圖11 有升起結構位移云圖

圖12 無升起結構位移云圖
分析關鍵結點有無側腳結構柱子底端的反力變化,如圖15,圖16所示。
根據上述有無升起結構的分析數據對比,顯然有升起結構的節點位移比無升起結構的節點位移要小;但在無升起結構的柱端反力隨外力逐漸增大時,小于又升起結構的柱底端反力,且二者之間的差值會逐漸增大。說明有升起建筑能夠有效地抵抗外力對柱子頂端產生側移的影響,但也會使得柱子底端產生應力集中現象,從而在外力增大時,使柱子首先破壞,造成嚴重后果。
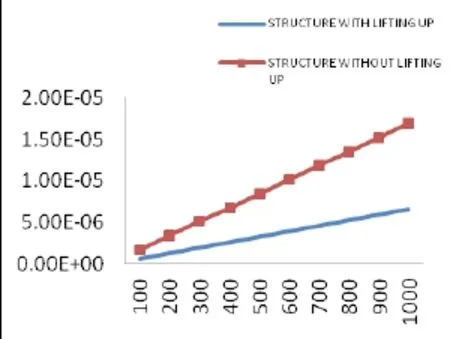
圖13 節點67 外力-位移圖

圖14 節點317外力-位移圖

圖15 節點1 外力-反力圖
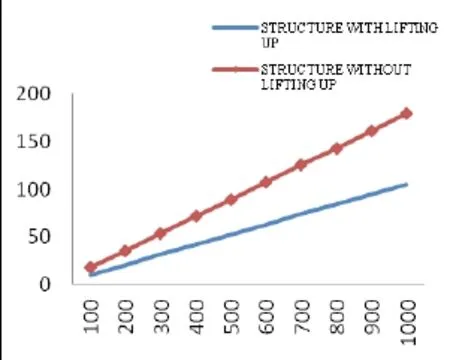
圖16 節點242外力-反力圖
結語
對于有無側腳的結構在受到相同水平外力的作用時,應用側腳的各個柱子頂端的側移小于沒有側腳的各個柱子頂端的側移;柱子底端的約束反力較沒有側腳的結構來說,有一定程度地減小,并且對比有無側腳結構在受到相同水平外力時的整體側移來看,有側腳的結構的整體側移要小于沒有側腳的結構。所以,側腳在結構中能夠有效地減弱外力對建筑的部分及整體的側移影響,減小結構本身在受外力過程中產生的反力,側腳可以有效的增加建筑結構抵抗外力的能力,增強建筑結構的整體性及穩定性。
升起結構能夠減弱各個柱子頂端在受到水平外力時產生的側移,但柱子底端的約束反力隨之增大,所以升起結構雖能夠有效地抵抗外力對建筑的影響,但對柱子強度要求有所提高。對于古建筑的維修,柱子底端的維護要加以重視。
王建省 張 建 王雪梅
北方工業大學土木工程學院
王建省,男,教授,研究方向:力學與古建筑結構、道橋結構工程;張建,男,本科生,土木工程專業;王雪梅,女,本科生,土木工程專業。
10.3969/j.issn.1001-8972.2016.11.048

