1 064 nm導模共振濾光片的設計與分析
李 坤,熊玉卿,王 超
(蘭州空間技術物理研究所 真空技術與物理重點實驗室,蘭州 730000)
1 064 nm導模共振濾光片的設計與分析
李坤,熊玉卿,王超
(蘭州空間技術物理研究所 真空技術與物理重點實驗室,蘭州730000)
為了獲得峰值波長為1 064 nm的反射型窄帶濾光片,采用導模共振原理進行設計,并利用嚴格耦合波法對濾光片的光譜特性進行了理論分析。首先設計了峰值波長1 064 nm單層反射型導模共振濾光片,由于覆蓋層和基底層的折射率不匹配,使得遠離峰值波長處的反射率偏高,引入減反射層后,峰值波長兩側的反射率明顯降低;其次分析了光柵層厚度、光柵周期對濾光片光譜性能的影響。結果表明設計的濾光片具有反射率高、帶寬窄及旁帶反射率低等優良的光學性能。
光學薄膜;濾光片;導模共振;減反射層
0 引言
濾光片是光學系統中比較常用的一種元件,傳統的制作方法是基于多層薄膜的干涉效應來實現,往往需要幾十層甚至上百層膜層才可以達到效果,給制備工藝帶來了一定的困難[1]。導模共振濾光片是基于導模共振效應來設計的,將光柵技術和傳統的薄膜技術相互結合,自從1992年Magnusson首次提出這一概念以來[2],由于其優良的光學特性及相對簡單的結構,一直是國內外光學領域研究的熱點之一[3-4]。所謂導模共振效應是指亞波長介質光柵在一定的結構參量和入射條件下出現的一種特殊衍射現象[5-6]。在物理機制上可認為是外部傳播的衍射場與受調制波導的泄漏波之間的耦合,當由周期結構所產生的某一衍射波與波導所支持的某一泄漏模位相匹配時,會產生共振異常現象,通常表現為共振波長處有極高的衍射效率和極窄的帶寬。
利用導模共振濾光片的光學性質,可以設計制作高反射、高透射光學元件[7~9]。結合傳統薄膜光學中的減反射層設計理論,可以設計在所需波長處具有高的反射率或透過率,而在其他波長處有寬截止帶的濾光片,還可以設計多通道濾光片和帶寬很窄的反射型或透射型濾光片,滿足多通道濾光片和超窄帶濾光片的需求。
1 設計理論
圖1是導模共振濾光片的結構示意圖,由光柵層和薄膜層組成,光柵層由兩種折射率分別為nH和nL的材料周期排列組成,光柵層的厚度為d1,光柵周期為T,填充系數為f。nC和nS分別是覆蓋層和基底層的折射率,其余薄膜層的折射率和厚度分別為nm和dm(m=2,3,……,M)。
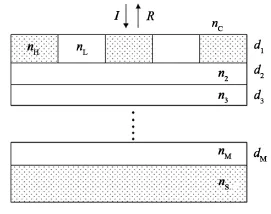
圖1 導模共振濾光片結構示意圖
當光柵周期T小于入射波長λ時,根據等效折射率理論,在TE偏振模式下,光柵層可以等效為一層均勻的介質薄膜,其等效折射率為[10]:
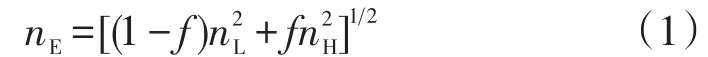
此時,利用平面波導理論近似分析導模共振濾光片中各參數的關系,多層波導結構的本征方程為[11]:
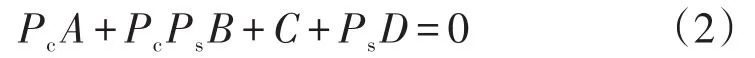
式2的A、B、C、D分別是特征矩陣的四個分量:
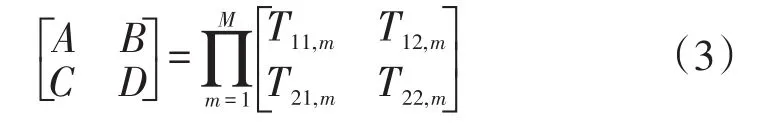
矩陣中各元素的含義如式(4):
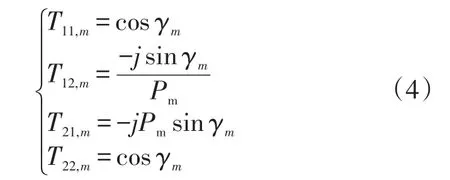
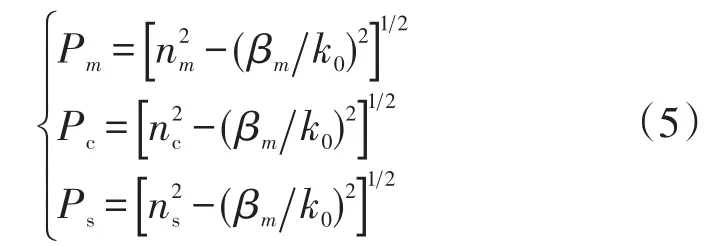
第m層的模傳播常數βm對所有膜層而言為一固定值,當出現共振峰時滿足關系式βm=βm/k0= nmsinθ-iλ/T,i是光柵的衍射級次(i=0,±1,±2,……),v是第m層的導模級次(v=0,±1,±2,……),T是光柵的周期,光柵層的等效折射率為nE。
出現導模共振效應時,滿足max(nC,nS)<βm<max(nm,E,m=1,2,3,……)。對于單層導模共振濾光片,即m=1時,可以得到最簡單的一種形式如式(6):
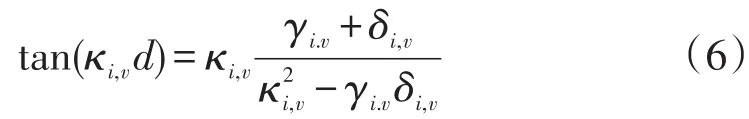
式中的參數為:
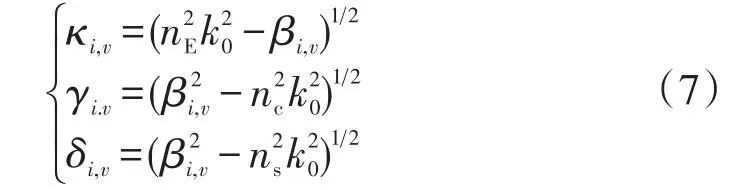
設計導模共振濾光片時,通常是用平面波導理論近似分析光柵層各參數的關系,然后利用嚴格耦合波法進行精確求解[12]。嚴格耦合波法是基于電磁場理論,在適當的邊界條件下嚴格的求解麥克斯韋方程組。
2 1 064 nm導模共振濾光片設計
對于圖1中的結構,當只有一層光柵層后,簡化為圖2的單層導模共振濾光片。在圖2的結構中,覆蓋層的折射率nC和基底層的折射率nS分別取1.0 和1.52,光柵周期T取640 nm,設計的峰值波長在1 064 nm,光柵層由兩種不同介質材料構成,高折射率nH為2.1,低折射率nL為1.9,占空比 f取0.5,光柵層厚度d1為214.6 nm,入射光以TE偏振模式垂直入射利用嚴格耦合波法精確計算單層導模共振濾光片的反射率曲線,如圖3所示。
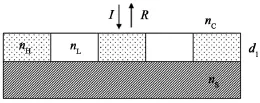
圖2 單層導模共振濾光片結構圖
從圖3的反射率曲線可看到,單層導模共振濾光片在峰值波長1 064 nm處幾乎有100%的反射率,并且帶寬小于10 nm,然而在峰值波長1 064 nm的兩側反射率較高,尤其是在1 100~1 250 nm波段,反射率幾乎達到20%,分析認為是由于覆蓋層和基底層的折射率不匹配造成的。
為了降低上述單層濾光片旁帶的反射率,利用光學薄膜中常用的減反射層設計方法,在單層濾光片和覆蓋層之間添加一層低折射率的層,其折射率為n2,厚度為d2,結構如圖4所示。
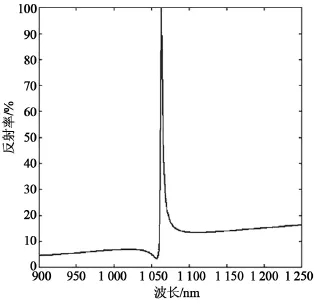
圖3 單層導模共振濾光片的反射率曲線圖

圖4 帶有減反射層的導模共振濾光片的結構圖
這里選折射率n2為1.38,減反射層的厚度滿足關系式d=,計算可得厚度d2應為193 nm。利用嚴格耦合波法計算的反射率曲線如圖5所示,可以看到相比于單層濾光片,在增加了減反射層之后,峰值波長兩側的反射率大大降低了。
3 導模共振濾光片的分析
對圖2中的單層導模共振濾光片進行分析,分別分析了光柵層厚度和周期變化對濾光片光譜性能的影響。
當光柵層的厚度從170 nm增加到230 nm時,利用嚴格耦合波法計算光譜曲線,光線以TE偏振模式正入射,得到圖6所示的光譜圖。隨著光柵層厚度的增加,反射率峰值波長向長波方向漂移,從1 031~1 074 nm,漂移43 nm,并且隨著光柵層厚度的增加,旁帶的反射率降低。
當光柵層的周期從600 nm增加到680 nm時,利用嚴格耦合波法計算光譜曲線,光線以TE偏振模式正入射,得到圖7所示的光譜圖。隨著光柵周期的增加,反射率峰值波長向長波方向漂移,從1 005~1121 nm,漂移116 nm,不過此時隨著光柵周期的增加,旁帶的反射率增加。
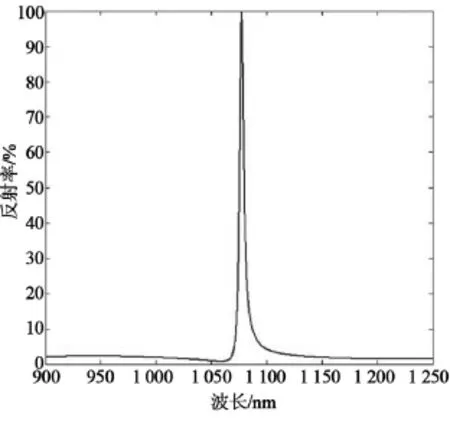
圖5 增加減反射層之后的導模共振濾光片的反射率圖
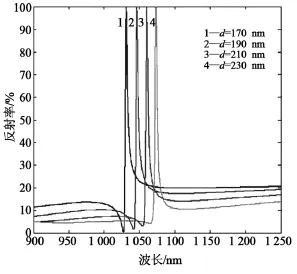
圖6 光柵層厚度變化對光譜的影響曲線圖
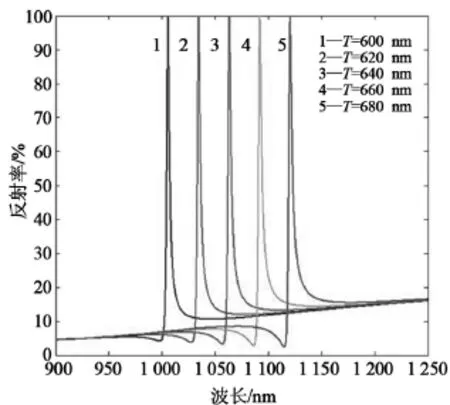
圖7 光柵周期變化對光譜性能的影響曲線圖
4 結論
文章基于導模共振效應設計了峰值波長位于1 064 nm的反射型濾光片。首先設計了單層反射型導模共振濾光片,然后通過增加減反射層的設計方法優化了其反射率光譜,在所要求的峰值波長1 064 nm處均得到了良好的光學特性。利用嚴格耦合波法分析了光柵層厚度、光柵周期和填充料率對濾光片性能的影響。
[1]熊玉卿.超窄帶濾光片制作技術[J].真空與低溫,2005,11 (3):125-130.
[2]Magnusson R,Wang SS.New principle for optical filters[J]. APL,1992,61(9):1022-1024.
[3]Tibuleac S,Magnusson R.Reflection and transmission guided-mode resonance filters[J].JOptSoc Am A,1997,14(7): 1617-1626.
[4]Magnusson R,ShinD,Liu ZS.Guided-mode resonanceBrewster filter[J].OptLett,1998,23(8):612-614.
[5]王琦,張大偉,陳家璧,莊松林.導模共振濾光片的研究進展[J].激光技術,2010,34(1):71-74
[6]Wang SS,Magnusson R.Theory and applicationsofguidedmoderesonance filters[J].Appliedoptics,1993,32(14):2606-2613.
[7]王振華,蔡強,陳強.無標記導模共振布儒斯特傳感器檢測靈敏度研究[J].光學學報,2014,34(6):35-40.
[8]王寬,熊玉卿,王濟洲,等.一種窄帶導模共振負濾光片的設計[J].真空科學與技術學報,2013,33(8)129-132.
[9]Ma J,Liu S,Zhang D,etal.Transmission guided-mode resonance filtersbased on high reflectionmultilayerstacks[J].Optik-International Journalfor Lightand ElectronOptics,2010,121(12):1144-1147.
[10]Rytov SM.Electromagnetic properties of a finely stratified medium[J].Soviet Physics JETP-USSR,1956,2(3):466-475.
[11]WangSS,Magnusson R.Multilayerwaveguide-grating filters [J].Applied optics,1995,34(14):2414-2420.
[12]周傳宏,王磊,聶婭,等.介質光柵導模共振耦合波分析[J].物理學報,2002,51(1):27-32.
DESIGN AND ANALYSISOF 1 064 nm GUIDEDMODERESONANCE FILTER
LIKun,XIONG Yu-Qing,WANG Chao
(Science and Technology on Vacuum Technology and Physics Laboratory,Lanzhou Instituteof Physics,Lanzhou730000,China)
In order to obtain a reflection filterw ith peak wavelength of 1064 nm,guided-mode resonance effectwas used.The spectrawere calculated by using rigorous coupled wavemethod.First,a reflection guidedmode resonance filter w ith peak wavelength at 1064 nm was designed by using a single layer structure.But the reflections in the range away from the peak wavelength were somewhathigh due to themismatch between the cover coating and substrate.By adding an antireflective layer,the reflections in the range away from the peak wavelength were reduced obviously.Then the grating thicknessand grating period effectson opticalpropertieswere analyzed.The resultshowed thatgood opticalproperties could be obtained by the design.
optic film;filter;guided-mode resonance;antireflective layer
O484+1
A
1006-7086(2016)03-0166-04
10.3969/j.issn.1006-7086.2016.03.009
2016-01-20
李坤(1988-),男,山東濟寧人,碩士,主要從事濾光片方面的研究。E-mail:likuncumt@126.com。

