矩陣向量相乘并行算法分析與實現
郝 靜 劉雅坤
中國石油大學(華東)理學院
矩陣向量相乘并行算法分析與實現
郝 靜 劉雅坤
中國石油大學(華東)理學院
矩陣運算是工程數值計算中一種常見的運算方式。大量的高維矩陣運算對數學計算提出了新的要求。本文針對行劃分,列劃分不同模式,給出OpenMPI算法的分析與實現,并得到按行劃分的優勢。
矩陣向量,并行,OpenMP;
一、問題背景與提出
矩陣向量相乘是數學以及工程中經常遇到的一種計算方式,矩陣向量乘法在許多解決實際問題中都有應用,但矩陣計算因其維數增大而造成的計算量增大是計算科學中需要進一步解決的問題。利用并行計算方法,將矩陣向量進行分發,使每個進程同時進行計算,將會大大減少計算的時間,提高計算效率。
并行計算(Parallel Computing)是指同時使用多種計算資源解決計算問題的過程,是提高計算機系統計算速度和處理能力的一種有效手段。它的基本思想是用多個處理器來協同求解同一問題,即將被求解的問題分解成若干個部分,各部分均由一個獨立的處理機來并行計算。現實社會中,越來越多的數據信息需要計算機處理,串行計算機程序技術已經不能滿足人們的需求,并行計算會越來越受到人們的青睞。
從一個串行程序得到一個并行程序的工作一般由四個步驟構成:1)將計算分解成任務:分解的主要目標就是要揭示足夠的并行性,從而盡量保持所有的進程在所有時間都忙,同時要注意由此引起的任務管理開銷不能太大。2)將任務分配給進程:分配的基本性能目標是在進程之間做負載平衡,要減少進程之間的通信量,還要減少運行時管理這種分配的開銷。3)在進程之間協調必要地數據訪問、通信和同步。4)將進程映射或綁定到處理器。本文就是將矩陣與向量相乘分解成向量與向量相乘,分發給幾個進程分別計算,將其并行化。
二、矩陣向量的串行算法描述
矩陣向量乘法是將一個mxn的矩陣A= (0≤i≤m-1,0≤j≤n-1)乘以nx1的向量B=得到一個具有m個元素的列向量C=。矩陣向量串行算法假設一次乘法和加法運算時時間為一個單位時間,則矩陣向量乘法算法的時間復雜度為O(mn),如果矩陣是方陣,那么復雜度就變為O()。
矩陣向量串行算法:

三、模型建立
矩陣并行計算時,將矩陣進行按行、列、塊三種方式進行劃分,矩陣和向量按進程個數進行分發,接收矩陣和向量的進程做相應的運算,最后將結果進行規約綜合。本文只討論進程個數恰能完全將矩陣向量平均分配的情況。
通過已有相關文獻的查閱,我們得知三種分法方式中,隨著維數的增高,按行劃分是最有效的方法;按列劃分在分發時需要分發的次數為維數的倍數,分發的時間將大大增加。按塊劃分需要將矩陣進行塊劃分,按塊劃分的優勢在矩陣與矩陣相乘的算法設計中優勢比較明顯。
在本文中,作者通過設計按塊劃分矩陣與向量相乘算法中發現,算法與按行、按列算法設計有很大的相似之處,所以,本文將著重考慮矩陣與向量相乘的按行與按列兩種算法并行的情況。
3.1按行劃分矩陣
矩陣向量相乘時,我們考慮nxn維矩陣A在n個進程間劃分的情況。將計算機進程編號為0,1,2…n-1。則每一個進程都會存儲1xn維矩陣。進程會存儲ai1,ai2,ai3…ain。并且負責計算。向量C的存儲方法與B相同。
考慮P(p<n)個進程的情況,每個進程存儲1×n/p維矩陣,每個進程的矩陣要與向量B相乘,所得的向量C與向量B的乘法類似。所得到的向量即為所求。通信時間為O(n/p),計算時間為O(n2/p)。
3.2按列劃分矩陣
按列進行劃分是對每一行進行劃分然后發送到每個進程上。我們考慮n×n維矩陣A在n個進程間劃分的情況。將計算機進程編號為0,1,2…n-1。對于矩陣的第一行,a11…a1n進行劃分,進程pi接收到元素的為a1i,每一行劃分后,進程pi接收到的元素為a1i…ani。進程pi做的計算為cj=aji×bj,j=1…n每一個進程都會得到一個向量,將每一個向量所對應的元素相加,即得到最終的向量c。
3.3按塊劃分矩陣
假設p2等于n,將矩陣劃分成不同的矩陣塊,每一個矩陣塊上的矩陣為p×p維。將劃分的矩陣塊發送到每一個進程,進程上進行p×p維矩陣與的乘法運算。然后將計算同一行的矩陣塊的進程結果相加,于同一列矩陣塊相組合,得到最終的結果。
四、矩陣向量的并行算法描述
4.1基于OpenMP的多核并行算法的設計
OpenMP是一種面向共享內存以及分布式共享內容的多處理器多線程進行編程語言,是一種能夠被應用于顯式指導多線程、共享內存并行的應用程序編程接口。OpenMP具有良好可移植性,支持多種編程語言。OpenMP的編程模型以線程為基礎,通過編譯指導語句來顯式地指導并行化,常用編譯指導語句有parallel、parallel for、parallel sections,通過特定的#pragma omp進行標示。
利用parallel進行并行的原理是編譯時將同一段代碼復制到每一個線程上編譯,然后在本線程上執行編譯好的程序。所有線程程序相同,但是執行效果不同,比如利用OpenMP封裝的內置函數omp_ get_thread_num()來獲得線程號,然后根據線程號完成不同任務。執行原理和WinAPI利用線程號相同,都是獲取線程號來分不同任務,只不過線程號獲取方式不同。利用編譯指導語句parallel執行并行計算是粗粒度的并行,并且在parallel的末尾有一個隱含的同步屏障,所有線程完成所需的重復任務后,將各個同步屏障匯合,然后可以從各個線程收集所需要的數據合成所需要結果。
利用parallel for 并行原理是采用工作分配的執行方式,將循環所需要工作量按一定方式分配到各個執行線程,所有線程執行工作總和是原串行完成工作量。此方式對一個確定并且完整的for循環進行分割,分割成多段在不同CPU上運行。
4.2按行劃分矩陣向量相乘
程序要點:
利用parallel指令的復制執行的方式,利用各個線程的ID號劃分了工作任務,將矩陣按行劃分分配給各個線程,通過獲取線程號來分布不同任務。
實現按行劃分的矩陣向量乘法的程序關鍵代碼如下:

4.3按列劃分的算法實現
程序要點:
利用parallel指令的復制執行的方式,利用各個線程的ID號劃分了工作任務,將矩陣按列劃分分配給各個線程,通過獲取線程號來分布不同任務。
實現按列劃分的矩陣向量乘法的程序關鍵代碼如下:

五、算法實現
5.1最終計算結果
進行上機實驗,開發環境為Microsoft Visual Studio 2010(旗艦版)
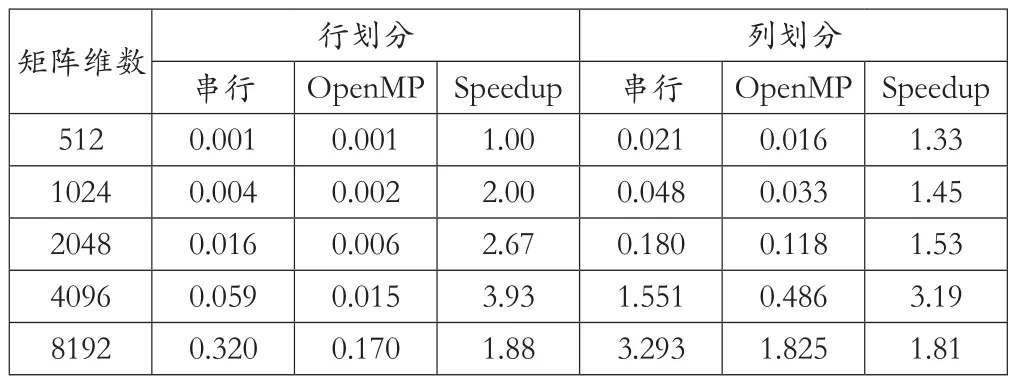
表一 4個進程計算結果(OpenMP)
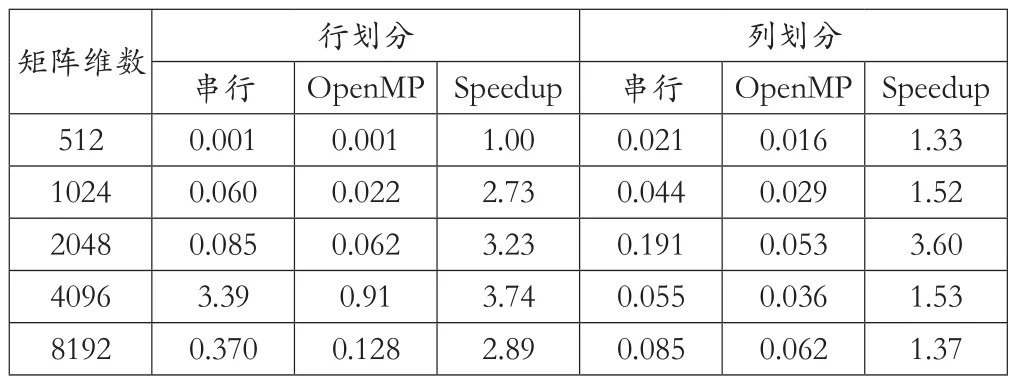
表二 8個進程計算結果(OpenMP)
六、數值實驗和結論
6.1圖表分析

圖一 4個進程計算結果加速比增長關系(openMP)
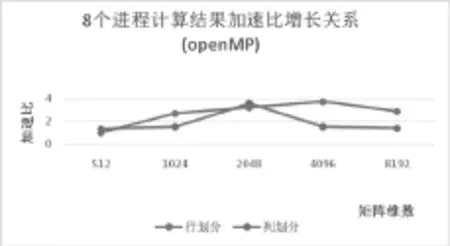
圖二 8個進程計算結果加速比增長關系(openMP)
6.2實驗結論
通過對上述圖表分析,我們可得到以下結論:
(1)OpenMP中隨著維數的增長,行劃分和列劃分方式加速比逐漸增長,但所用的進程數目較大時,加速比和效率較為明顯,因為線程數目越大,每個線程分配的任務量相對越小,運行效率越快。
(2)隨著維數的增高,按行劃分是相對有效的方法。按列劃分在分發時需要分發的次數為維數的倍數,分發的時間將大大增加。按列劃分需要將矩陣進行塊劃分。然后再進行分發,相對來講,增大了時間的消耗。
(3)在工程計算中,當矩陣維數較大時,可以采取按行劃分的方式大大增加計算速度,而當矩陣維數較小時,建議使用串行算法。
[1] 朱建偉.多線程并行快速求解e值的六種方法[J].現代計算機:普及版.2013(17).15-20
[2]多核系列教材編寫組.多核程序設計[M].北京.清華大學出版社,2007
[3] 鄧倩妮.并行程序設計導論[M].北京.北京機械工業出版社.2012.8
[4]尚智,陳碩.大型矩陣相乘并行計算的特性分析[J].Software Engineering,2013.02(1):15-19
郝靜(1994—),女,漢族,山東煙臺人,中國石油大學(華東)理學院,2013級本科生,數學與應用數學專業
劉雅坤(1995—),女,漢族,山東青島人,中國石油大學(華東)理學院,2013級本科生,數學與應用數學專業

