基于社交網絡的MMORPG玩家流失分析與預測

丁　軍　高大啟　薛程元　陳小紅

1(華東理工大學信息科學與工程學院　上海 200237)2(盛大游戲數據中心　上海 201203)

?

基于社交網絡的MMORPG玩家流失分析與預測

丁軍1高大啟1薛程元1陳小紅2

1(華東理工大學信息科學與工程學院上海 200237)2(盛大游戲數據中心上海 201203)

針對大型多人在線角色扮演游戲MMORPG(MassiveMultiplayerOnlineRole-PlayingGame)的玩家流失分析與預測問題，采用Cox比例風險模型建立玩家的流失模型，對玩家流失的因素進行分析，并對流失進行預測。分析玩家在游戲中的社交網絡的特征(玩家的好友關系、二度好友關系、好友間聊天情況)對玩家流失行為的影響。對盛大“星辰變”游戲數據的實驗表明，游戲中玩家所處的社交網絡對玩家的流失行為具有顯著影響，并能夠提高預測效果。與支持向量機、Logistic回歸和樸素貝葉斯分類進行對比，表明Cox模型更加適用于該玩家流失預測問題。

流失分析流失預測Cox回歸社交網絡在線角色扮演游戲

0　引　言

在保險業、醫療保健行業、信用卡、互聯網服務行業、通信行業等擁有長期穩定客戶的行業中，客戶的保留對公司的利潤有著驚人的影響[1]。因而，國內外已有許多面向上述行業的客戶流失分析與預測的相關研究。

近年來，大型多人在線角色扮演游戲MMORPG行業得到飛速發展。在MMORPG中，玩家扮演、控制某個角色，在虛擬世界中可以進行殺野怪升級、購買武器裝備等行為；玩家之間也可以進行交互，如道具交易、組隊完成任務、互相攻擊等。游戲的運營商通過對玩家定期收費，或者對購買虛擬道具進行收費。近幾年來，MMORPG的玩家數量急劇增長，據統計，2013年上半年中國國內MMORPG游戲收入突破142億人民幣。因而，游戲行業中各個公司、產品之間的玩家資源競爭日漸激烈。Kawale等[2]指出，吸引新的用戶加入游戲比挽留老用戶的代價大的多。所以，研究MMORPG中的玩家流失分析與預測具有重要意義。

Haenlain[3]、Ngonmang[4]、Nitzan[5]等相關研究均表明，在電話通信行業當中，客戶所在的社交網絡的特征對客戶的流失行為有顯著影響。而在MMORPG中，玩家之間有存在許多交互行為，玩家與玩家之間可能會加為好友，然后進行聊天互動、交易等，這使玩家之間形成了虛擬世界中的社交網絡，它與現實世界的社交網絡十分相似。

因此，本文針對MMORPG，在考慮玩家的個人屬性和行為特征的同時，引入玩家在游戲中的虛擬社交網絡的特征，建立流失分析與預測模型，以分析這些社交網絡特征對玩家流失行為的影響，并對流失趨勢進行預測。通過Cox比例風險模型，分別只使用個人屬性行為特征、社會網絡特征以及所有特征來建立流失分析模型。在盛大集團“星辰變”游戲數據上的實驗表明，玩家的社交網絡特征對玩家的流失行為具有顯著影響，并能夠明顯提高流失的預測效果；實驗中還將上述模型與SVM、Logistic回歸、NaiveBayes等分類方法進行對比，對比采用準確率、召回率、F值指標，結果表明，針對本文實驗數據的玩家流失預測，采用Cox回歸最為有效，預測效果較好。

1　基于Cox回歸的玩家流失分析模型

數據挖掘方法在其他行業的客戶流失的研究中得到了廣泛應用。例如Logistic回歸、支持向量機SVM等模式分類方法[1,6-8]，以及生存分析中的Cox比例風險模型[9,10]等。相對于模式分類方法，采用Cox回歸分析和預測玩家流失，具有以下優點：(1) 玩家的行為特征通常會隨時間變化，而Cox回歸模型能夠基于縱向數據進行建模，更加充分地利用這些依時間變化的協變量所包含的信息。(2) 能夠處理刪失數據(刪失數據是指在觀察或試驗中,由于人力或其他原因未能觀察到所感興趣的事件發生，如個體死亡、玩家流失)。既能夠考慮到觀測截止時已經流失的玩家，也能夠利用尚未流失的玩家信息，提高模型的有效性。因此，本文利用Cox比例風險模型對玩家的流失進行建模。

1.1生存函數與風險函數

生存時間，或者某事件出現的時間，通常用生存函數、概率密度函數和風險函數這三種形式來描述[11].

生存函數即累計生存概率。設T表示生存時間，F(t)=P(T≤t)表示T的分布函數(即個體生存時間長于t的概率)。則生存函數表示生存時間T超過給定值t的概率：

S(t)=1-F(t)=P(T>t)

(1)

概率密度函數的定義是：

(2)

風險函數λ(t)用于表示處于一定時刻t的個體是否容易死亡，它完全刻畫了t的分布，因而直接決定了概率密度函數和生存函數，在生存數據分析中起著非常重要的作用。其定義為：

(3)

當生存時間T的概率密度已知時，λ(t)可以按如下形式來表示：

(4)

上述關系式表明，生存函數、概率密度函數和風險函數實際上是等價的，已知三者之一，即可導出另兩個。

1.2Cox比例風險模型

Cox回歸模型或Cox比例風險模型，在1972年由Cox提出[12]。起初主要應用于臨床醫學及流行病學，由于其適應性極強等特點，被應用于許多研究領域。

不失一般性，當協變量均隨時間變化時，Cox模型的形式為：

h(t)=h0(t)exp(βTZ(t))

其中，Z(t)是依時間變化的協變量，β是回歸系數向量，h0(t)是未知的基準風險函數，只與時間有關，它對應于所有協變量為0時的流失風險，與協變量無關。Cox模型不對h0(t)的分布形式做任何假設，應用范圍十分廣泛，它又被稱為半參數模型[13]。

設S0(t)為t時刻的基準生存函數，則對應的累計生存函數為：

S(t)=S0(t)exp(βTZ(t))

每一時刻的基準風險通常用Kalbfleisch-Prentice[14]方法來估計。為了進行預測，我們需要在此基礎上估計基準風險函數與時間的顯式的關系式。通常假設(流失)事件發生的時間服從Weibull分布，記累計基準風險函數為：

那么累計基準風險函數與時間的關系為[15]：

logH0(t)=a0+a1log(t)

利用最小二乘法可以上式進行參數估計，從而能夠得到之后一個月的生存概率。代入未來數據，可以對玩家的流失概率進行預測。

2　實驗數據與特征描述

2.1實驗數據

本文實驗數據來自盛大集團的“星辰變”游戲。該游戲于2011年9月29日開始公開測試，其新服務器不斷增開，版本持續更新，保持著較高的人氣。本文選取該游戲“華中電信一區”的“逆央境”組，自2012年4月至2012年10月的數據。該區組在這一時間段內沒有區、組的合并操作，相對比較穩定，玩家數目較多。我們限定玩家的注冊時間在2012年4月之前。本文認為在某一月份當中有登錄記錄的玩家即為“活躍玩家”，否則斷定其已經流失。流失是指當月沒有活躍行為的玩家。

2012年4月的數據共包含活躍玩家6215名。在這些玩家的基礎上，之后每月的活躍玩家剩余數量變化如圖1所示，到2012年10月這些玩家當中有1653名尚未流失。

圖1　星辰變華中電信一區逆央境4月起玩家留存數

2.2特征選取

2.2.1虛擬社交網絡特征

本文通過玩家的好友列表構建社交網絡。即玩家為網絡中的節點，玩家與玩家之間有邊相連，表示他們在游戲中互相加為好友。基于這一網絡，本實驗采用下述特征，以分析玩家的社交網絡對玩家流失行為的影響：

1) 活躍/流失好友數

玩家的好友的流失行為可能會對玩家的流失風險產生影響，例如某幾個好友的流失可能使得玩家也不愿繼續游戲，所以首先考慮玩家的好友數的變化這一因素。在網絡中，活躍好友數即玩家對應節點的鄰居節點數目，或節點的度。用ISNi,t表示玩家i在月份t的鄰居節點集合，即玩家的好友列表中的所有好友的集合，那么玩家i在月份t的活躍好友數active_neighbori,t可記為：

我們用x1表示這一變量。并且其中：

類似地，每個月的已經流失的好友數為：

2) 二度好友關系

IritNitzan[5]在其關于電信行業客戶流失的研究中表明，社交網絡中度更高的客戶在網絡中的影響力更大，對其鄰居的影響更強。依據這一結論，我們考慮二度好友關系，即分別統計流失和未流失好友的好友數目。

用active_second_neighbor表示活躍好友的活躍好友數目，則：

x3=active_second_neighbori,t

同理，每個月已經流失好友的好友數為：

3) 聊天數目

好友之間的關系越密切，他們之間的相互影響也會越大。本文通過好友之間的聊天數目來表示好友之間的關系強度。好友之間發送/接收到一條消息，聊天數記為1，分別對玩家與當月的活躍好友，以及與本月已經流失的好友，前一個月的聊天記錄數分別為：

其中，chati,j,t表示玩家i與玩家j之間，在月份t當中的聊天信息總數。

2.2.2個人屬性與行為特征

除了上述本文主要研究的虛擬社會網絡因素之外，我們還加入玩家的個人角色屬性以及在游戲中的行為特征，描述如下：

x13：玩家的游戲角色性別。

x8：角色等級，從1級至70級。

x9：角色的職業。“星辰變”中共有6個角色。

x10：玩家角色當月的登錄游戲次數。

x11：當月殺死其他玩家角色次數。

x12：當月殺死怪物、靈獸以及非玩家角色次數。

x13：當月被玩家角色擊殺次數。

x14：被怪物、靈獸以及非玩家角色擊殺次數。

x15：角色當月花費金幣總量。

x16：角色當月花費金幣次數。

x17：角色當月花費星幣總量。

x18：角色當月花費星幣次數。

x19：角色當月與其他玩家角色組隊次數。

上述屬性與行為特征能夠表示玩家角色的狀態、心態以及對游戲的參與程度，我們認為它們可能成為玩家流失的影響因素。這樣，本文共考慮19個特征，包含6個社交網絡特征以及13個個人屬性與行為特征。

2.2.3特征篩選方法

前文所介紹的特征數目較多，其中有些特征可能與玩家流失的相關性較大，而另一些特征可能與玩家的流失并無明顯關聯，所以需要對這些特征進行篩選，去除冗余特征。本文使用Cox回歸中最常使用的Z檢驗，進行一次篩選，來實現這一目的。

Z檢驗的零假設和替換假設分別為：

H0:βk=0,其它參數βi(i≠k)固定

H1:βk≠0,其它參數βi(i≠k)固定

當H0成立時，Z統計量Z=βk/SE(βk)應服從標準正態分布，其中SE(βk)為回歸系數βk的標準誤差。通過Z統計量對應的概率值，可以推斷出變量與玩家流失關系的顯著性。

3　實驗與結果分析

本文在R語言環境中，利用“coxph”包所實現的Cox回歸模型進行實驗，當中的“basehaz”函數實現了Kalbfleisch-Prentice估計。

3.1特征的相關性檢驗及篩選

在數據預處理階段，我們將表中除性別之外的所有特征進行標準化和中心化，以提高模型的擬合效果，以及便于對各個特征對流失的影響程度進行比較。將處理后的數據代入Cox模型，訓練結果的各個特征的系數及檢驗結果見表1所示。其中，第二列為回歸系數，第三列為系數以e為底的冪值，第四列為Z統計量對應的概率值。

表1　所有特征的系數及Z檢驗結果

我們設定顯著性水平為0.5，則篩選出的特征為：職業(x9)、登錄次數(x10)、被其他玩家擊殺次數(x13)、金幣消費總數目(x15)、金幣消費次數(x16)、組隊次數(x19)、活躍好友數(x1)、流失好友數(x2)、活躍好友二度好友數(x3)、流失好友二度好友數(x4)、流失好友上月聊天次數(x6)。在這一實驗中，在6個社會網絡特征中，有5個對玩家流失具有顯著影響。特征篩選方法適合于其他的模型，都可以通過模型的特征系數的顯著性來進行篩選。

3.2特征的相關性檢驗及篩選

利用上述篩選出的特征，構建Cox回歸模型：

模型1：

其中，f(x)=exp(βTx)。對模型1進行擬合，得到擬合系數結果如表2所示，系數絕對值對比如圖2所示。在所有篩選出的特征當中，系數的絕對值最大的是玩家當月金幣的使用次數，為-2.76，對流失的影響程度最大，花費金幣次數越多，玩家的流失風險越低。其次是登錄次數，也是登錄次數更多的玩家，流失風險更低。

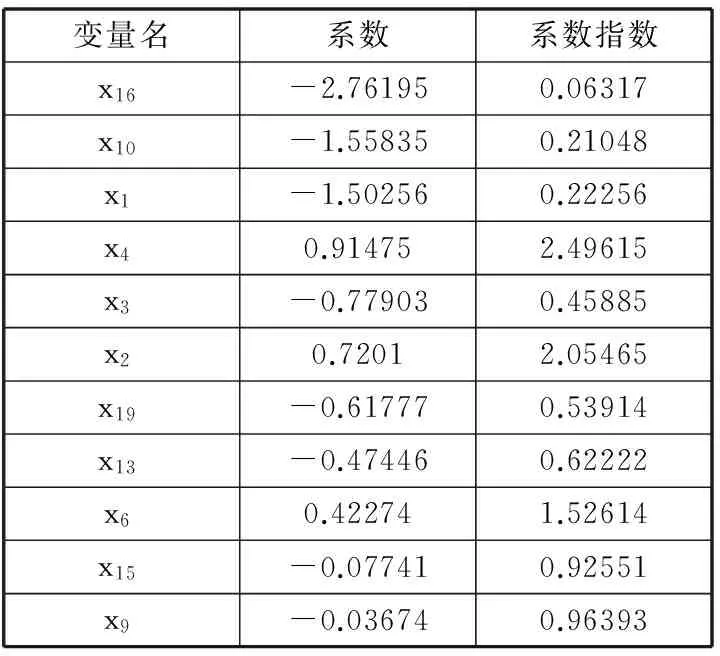
表2　模型1擬合系數

圖2　模型1擬合系數絕對值柱狀圖

玩家在游戲中的社會網絡特征當中，活躍好友數、流失好友的好友數、活躍好友的好友數以及流失好友數對玩家流失的影響都相對比較大。其中，活躍的好友數的系數(x1)為負(-1.503)，流失好友總數的系數為正(x2, 0.720)，說明玩家的活躍好友對玩家的行為具有正面影響；反之，流失好友的增多也會使玩家容易隨之一起流失。活躍和流失好友對應的二度好友數這兩個特征的系數(x3和x4,分別為-0.779和0.915)則表明，一個玩家的好友數能夠對其好友的行為產生影響，它可以在一定程度上代表玩家在社會網絡中的影響力，這也印證了文獻中的觀點。除此以外，社會網絡特征中的玩家與流失好友在前一個月的聊天數目(x6, 系數為0.423)也對其流失行為有顯著影響，聊天數目越多，說明玩家與好友之間的關系越密切，因此好友的流失對玩家的影響也會更大，擬合結果正印證了這一點。這些結果說明，玩家在游戲中的社交網絡的特征對玩家的流失行為的影響是顯著的。

比較出乎意料的結果是被玩家擊殺次數的系數為負(x13, -0.474)，我們可以解釋為，通常被其他玩家殺死次數多的玩家，游戲的參與度相對更高，更不容易流失。

3.3生存函數估計

通過Kalbfleisch-Prentice估計得到5～9月基準生存函數，如圖3所示。5月的生存函數值為0.959，而到9月，這一數值降到了0.607。用1.2節介紹的方法進行擬合，擬合結果的修正R方為0.9991，F統計量對應的概率為8.045×10-6，表明采用這一方法的擬合效果是十分滿意的。代入10月的數據，并利1.2節介紹的方法，基準生存函數值0.526。

圖3　基準生存函數曲線圖

3.4玩家流失預測

為了作為對比，我們還分別只使用玩家的個人屬性與行為特征，以及只使用社會網絡特征來構建模型。

模型2：只考慮玩家的個人屬性以及行為特征：

h/h0=f(x9,x10,x13,x15,x16,x19)

模型3：只考慮社會網絡特征：

h/h0=f(x1,x2,x3,x4,x6)

3.4.1評價指標

如表3所示，有tp個類別為流失的樣本被模型正確判定為流失，fn個類別為流失的樣本被模型誤判定為類別未流失，有fp個類別為未流失的樣本被模型誤判斷定為流失，tn個類別為未流失的樣本被模型正確判為未流失。

表3　準確率和召回率

Precision=tp/(tp+fp)，又稱“精度”、“正確率”，反映了被模型判定的流失玩家中真正的流失玩家的比重。

Recall=tp/(tp+fn)，又稱“查全率”，指的是所有真實流失的玩家中被模型判定為流失的比重。

Precision和Recall都是評估流失模型的重要指標。F值是Precision和Recall的加權調和平均，F= 2×召回率×準確率/(召回率+準確率)，F值是模型的一個綜合評估指標。

3.4.2模型評估

表4為使用三個Cox回歸模型以及SVM、Logistic回歸和樸素貝葉斯分類器對玩家的流失做預測的評價結果，我們分別計算出準確率、召回率和F值。

Cox回歸模型如前文所述，用4～8月的數據來進行擬合，再用9月的數據來預測10月玩家的流失情況，我們設定概率閾值為基準流失函數值；類似的，在后三個分類方法中，將表列出的特征，4～8月每個月的數據分別作為分類器里的一個特征，進行訓練，預測時，則采用5～9月的數據，對10月進行預測，SVM采用Sigmoid核。

表4　10月份玩家流失預測對比

在Cox回歸的三個模型中，只采用玩家個人屬性與行為特征時，召回率比較高(0.992)，但是準確率只有0.234；而引入了玩家的社交網絡特征的模型1，預測的準確率達到0.753，召回率為0.824，其F值為0.393，綜合效果好于前者。而只采用社會網絡特征時(模型3)，預測結果的準確率和召回率均略低于0.5。通過對比可以看到，玩家的個人特征與社交網絡特征，對流失預測具有互補的作用，當綜合使用兩方面的特征，預測結果顯著高于僅僅使用一類特征時的結果。采用模式分類方法的實驗中，SVM與Logistic回歸的預測準確率較Cox模型高，而召回率低；樸素貝葉斯分類的結果則與前兩者相反。通過F值的對比，Cox回歸模型更加適用于本文的玩家的流失分析與預測。

4　結　語

MMORPG玩家的流失對游戲運營商的收益具有重要影響。本文采用Cox比例風險模型建立MMORPG游戲玩家流失分析模型，對“星辰變”游戲玩家的流失行為進行分析，并具體分析了游戲中的社會網絡因素對玩家流失行為的影響。實驗結果表明，玩家在游戲里社交網絡中的玩家特征和流失行為對玩家的流失行為有顯著影響。引入這些特征能夠顯著提高流失預測效果，并且Cox回歸模型更加適用與本文的MMORPG玩家流失預測問題。

[1] 應維云,覃正,趙宇.SVM方法及其在客戶流失預測中的應用研究[J].系統工程理論與實踐,2007,27(7):105-110.

[2]KawaleJ,PalA,SrivastavaJ.ChurnpredictioninMMORPGs:Asocialinfluencebasedapproach[C]//ComputationalScienceandEngineering,2009.CSE’09.InternationalConferenceon.IEEE,2009,4:423-428.

[3]HaenleinM.Socialinteractionsincustomerchurndecisions:Theimpactofrelationshipdirectionality[J].InternationalJournalofResearchinMarketing,2013,30(3):236-248.

[4]NgonmangB,ViennetE,TchuenteM.Churnpredictioninarealonlinesocialnetworkusinglocalcommunityanalysis[C]//Proceedingsofthe2012InternationalConferenceonAdvancesinSocialNetworksAnalysisandMining(ASONAM2012).IEEEComputerSociety,2012:282-288.

[5]NitzanI,LibaiB.Socialeffectsoncustomerretention[J].JournalofMarketing,2011,75(6):24-38.

[6]HuangB,KechadiMT,BuckleyB.Customerchurnpredictionintelecommunications[J].ExpertSystemswithApplications,2012,39(1):1414-1425.

[7] 蔣國瑞,司學峰.基于代價敏感SVM的電信客戶流失預測研究[J].計算機應用研究,2009,26(2):521-523.

[8]DasguptaK,SunghR,ViswanathanB,etal.Socialtiesandtheirrelevancetochurninmobiletelecomnetworks[C]//Proceedingsofthe11thinternationalconferenceonExtendingdatabasetechnology:Advancesindatabasetechnology.ACM,2008:668-677.

[9] 鄧森文,馬溪駿.基于Cox模型的移動通信行業中低端客戶流失預測研究[J].合肥工業大學學報:自然科學版,2010,33(11):1698-1701.

[10] 鄭浩,趙翔.基于生存分析的顧客流失預測及挽救效果研究[J].生產力研究,2011(1):97-99.

[11]KalbfleischJD,PrenticeRL.Thestatisticalanalysisoffailuretimedata[M].JohnWiley&Sons,2011.

[12]CoxDR.Regressionmodelsandlifetables[J].JRstatsocB,1972,34(2):187-220.

[13] 王啟華.生存數據統計分析[M].北京:科學出版社,2007.

[14]WengYP,WongKF.Baselinesurvivalfunctionestimatorsunderproportionalhazardsassumption[D].InstituteofStatistics,nationalUniversityofKaohsiung,2007.

[15]RoystonP,ParmarMKB.Flexibleparametricproportional-hazardsandproportional-oddsmodelsforcensoredsurvivaldata,withapplicationtoprognosticmodelingandestimationoftreatmenteffects[J].Statisticsinmedicine,2002,21(15):2175-2197.

CHURNANALYSISANDPREDICTIONFORSOCIALNETWORK-BASEDMMORPGPLAYERS

DingJun1GaoDaqi1XueChengyuan1ChenXiaohong2

1(School of Information Science and Engineering,East China University of Science and Technology,Shanghai 200237,China)2(Data Centre,Shandagames,Shanghai 201203,China)

FortheproblemofanalysingandpredictingplayerschurninginMMORPG(MassiveMultiplayerOnlineRole-playingGame),webuiltachurnanalysismodelusingCoxproportionalhazardmodeltostudythefactorsofplayerschurning,andtopredictthechurningaswell.Specifically,weanalysedtheimpactsofsocialnetworksfeaturesofplayersinthegame(players’friendships,secondarydegreefriendshipsandchatsbetweenfriends)onplayers’churningbehaviours.Experimentsonthegameof“StarsVariation”ofSDOshowedthatthesocialnetworkstheplayerslocatedingamesignificantlyaffectedthechurningbehavioursofplayers,andcouldimprovetheeffectofprediction.Incomparisonwithsupportvectormachine,LogisticregressionandnaiveBayes,theCoxmodelisprovedmoresuitablefortheplayerschurnpredictiontask.

ChurnanalysisChurnpredictionCoxregressionSocialnetworksMMORPG

2014-08-27。丁軍，博士生，主研領域：數據挖掘。高大啟，教授。薛程元，碩士生。陳小紅，本科。

TP311

ADOI:10.3969/j.issn.1000-386x.2016.03.024