基于時間序列分析的港口集裝箱吞吐量預測分析

孔琳琳，劉　瀾，許文秀，吳金卓*

(1.東北林業大學 工程技術學院 哈爾濱 150040；2.湖南工學院，湖南 衡陽 421002)

?

基于時間序列分析的港口集裝箱吞吐量預測分析

孔琳琳1，劉瀾2，許文秀1，吳金卓1*

(1.東北林業大學 工程技術學院 哈爾濱 150040；2.湖南工學院，湖南 衡陽 421002)

集裝箱運輸是現今國際運輸的主要方式之一，長期監測港口集裝箱吞吐量并對未來趨勢進行相關的預測研究，對于港口基礎設施建設、區域經濟發展以及國家戰略發展方面都有著非常深遠的意義。本文針對影響港口集裝箱吞吐量復雜性因素的非線性特點，以中國某港口2001年1月至2014年12月共14 a的集裝箱吞吐量數據為例，利用統計分析軟件R對該港口集裝箱吞吐量數據進行時間序列分析，提出了一個合理的ARIMA模型來描述集裝箱吞吐量的變化，并對模型進行檢驗優化，應用該模型預測十個月后的集裝箱吞吐量數據。結果表明，利用統計分析軟件R對港口集裝箱吞吐量數據進行時間序列分析后得到的預測模型可以很好的描述港口集裝箱吞吐量變化情況，據此可以為港口在不同時期制定最優措施提供參考。

集裝箱吞吐量；時間序列分析；預測；模型

0　引　言

港口作為一個重要的交通樞紐，是各種交通工具的轉換中心，大量貨物聚集在此，不僅能促進當地經濟的發展，而且也能拉動港口周邊地區的工業發展，在一個國家的經濟發展中發揮著至關重要的作用[1-2]。港口吞吐量這一指標就是反映一定時間內(一般為1 a)港口生產經營活動規模以及國家和地區經濟發展狀況的參考指標，對港口的建設和管理具有重大的影響。

港口吞吐量分為衡量旅客流動情況的旅客吞吐量和衡量貨物流動情況的集裝箱吞吐量兩種。長期監測港口集裝箱吞吐量并對未來趨勢進行相關的預測研究，對于港口基礎設施建設、區域經濟發展以及國家戰略發展方面都有著非常深遠的意義[3-4]。翟希東[5]采用灰色理論模型和改進的神經網絡模型結合的方法建立港口集裝箱吞吐量預測模型，并以大連港集裝箱吞吐量的實際發生數據為實驗樣本，驗證了提出的集裝箱吞吐量預測模型的有效性和實用性。黃維忠[6]為避免以往研究中吞吐量的預測值與實測值之間差距較大的情況，突破性地提出了一種動態預測方法對吞吐量進行預測，并以上海港為實例驗證了此方法的可行性。江艦等[7]以大連港為例對集裝箱吞吐量的影響因素以及其產生的經濟影響進行計量分析，并建立了港口城市GDP與進出口商品總值對集裝箱吞吐量影響的二元線性回歸模型，從而很好地解釋了其中的關系，也對國內其他港口城市起到了很好的借鑒意義。

市場經濟、自然條件、國家政策等因素都是影響集裝箱吞吐量的重要因素。由于這些因素具有極強的復雜性而不能用精確的語言來描述其作用機制，屬于非線性系統問題，因此這些因素最終都會反饋在其時間序列上[8-9]。由此可見，對港口集裝箱吞吐量建立時間序列進行分析不僅有利于了解集裝箱吞吐量隨季節變化的趨勢，而且對其建模和預測有一定的指導意義。

本文采用統計分析軟件R對國內某港口2001年1月～2014年12月的集裝箱吞吐量進行時間序列分析，通過分析其季節性數據，確定吞吐量與季節變化之間的關系。通過建立ARIMA模型預測該港口十個月后的集裝箱吞吐量數據，結合預測結果分析未來一段時間內港口吞吐量隨季節變化的規律，對港口在不同時期制定最優措施提供參考。

1　研究方法

1.1時間序列分析

時間序列是指將一組數據按照時間推移的順序進行排列。這些長時間的數據反映出來的整體向上或向下的趨勢、在一年內隨季節變化的情況、一段時間內呈現出的漲落相同的循環波動和無規律的隨機波動4種變化情況構成了時間序列的4要素[10-12]。應用數理統計方法可以對具有時序性和相關性的時間序列進行分析，通過建模還可以預測事件未來的發展趨勢及走向[13-15]。

本文利用R軟件中的時間序列分析對某港口集裝箱吞吐量進行分析。R軟件是一個具有相關統計分析和作圖功能的綜合軟件，其編程語言簡單實用，作圖功能強大，統計分析能力突出，可移植性強，同時還具有強大的數據存儲和處理系統以及數組運算工具。其完整而連貫的統計分析工具非常適合用來做時間序列圖來分析。根據R軟件作出的時間序列圖，分析數據的周期性變化，并對時間序列進行分解。對數據進行季節性修正，把季節性部分從原始時間序列中去除，可以得到僅包含趨勢部分和不規則部分的季節性修正時間序列圖。

1.2時間序列建模與預測

本文選用自回歸積分滑動平均模型ARIMA(p，d，q)來建立港口集裝箱吞吐量的時間序列模型，通過時間序列的差分，得到一個合適的ARIMA的模型，以此來預測2015年前十個月的港口集裝箱吞吐量[16]。ARIMA(p，d，q)模型是為平穩的時間序列定義的，對于非平穩時間序列，需要進行差分，變為差分平穩序列后才能應用該模型。差分平穩序列可以用ARIMA(p，d，q)模型進行擬合。該模型的結構表示為：

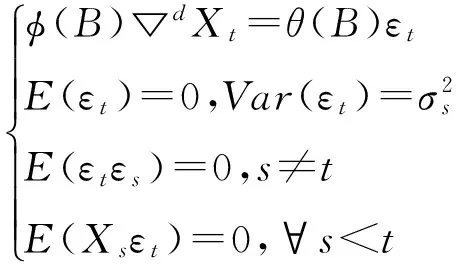
(1)

對d階齊次非平穩序列{Xt}而言，{▽dXt}是一個平穩序列，設其適合ARIMA(p,d,q)模型，即

φ(B)▽dXt=θ(B)εt。

(2)

或者

φ(B)(1-B)dXt=θ(B)εt。

(3)

其中

φ(B)=1-φ1B-φ2B2-…-φpBp。

(4)

為消除季節性影響和長期趨勢影響，對該序列作一階12步差分，檢驗序列是否平穩。如果時間序列平穩，就可以使用ARIMA(p,d,q)模型，其中d=1。

2　實例分析

2.1某港口集裝箱吞吐量的時間序列分析

本文收集并整理了中國十大港口之一的某港口2001年1月至2014年12月集裝箱吐吞量的數據，利用統計分析軟件R對數據進行統計分析。首先，將數據讀入到R中，繪制時間序列圖，得到該港集裝箱吞吐量時間序列圖如圖1所示。

由圖1可知，該港口集裝箱吞吐量時間序列總體呈現上升趨勢，并且存在著一定的周期性變化。這個季節性時間序列由趨勢部分、季節性部分和不規則部分3部分組成。

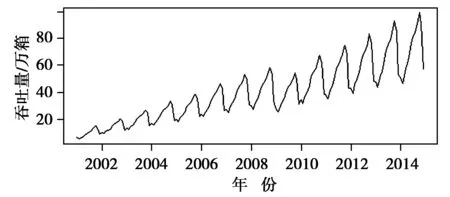
圖1　某港口集裝箱吞吐量時間序列圖Fig.1 Time sequence chart of the handling capacity in a port

通過對時間序列的趨勢的、季節性和不規則部分進行分析，得到了每年 1～12 月的季節性因素。季節性因素最大值在十月，最小值在二月，一、二、三、四、五、十二月集裝箱吞吐量較少，標志著每年的峰值在十月，低谷在二月份。繪制出時間序列中估計的趨勢、季節性和不規則的部分，時間序列的分解結果如圖2所示。圖2共分為4個部分，由上至下分別為：原始的時間序列圖以及估計的趨勢圖、季節性圖和不規則圖。由圖2可知，估計出的趨勢部分從2001年開始逐年穩步上升，在2009年前后有下降的趨勢，但隨后又持續穩步上升。圖2估計出的季節性部分圖像穩定，說明該港口集裝箱吞吐量存在一定的季節性規律，與前文分析相符。

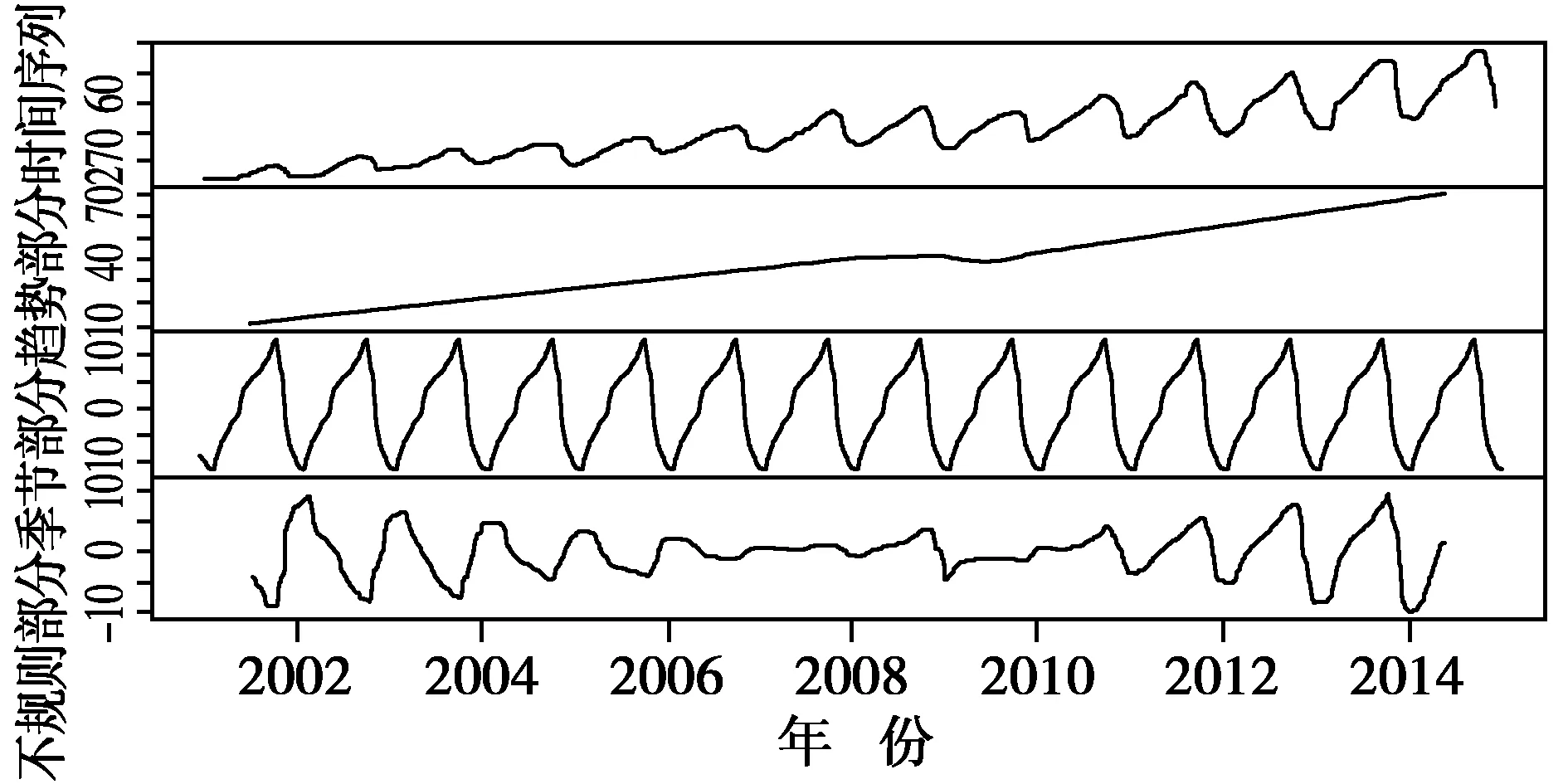
圖2　時間序列的分解Fig.2 Decomposition of time sequence

對數據進行季節性修正，把季節性部分從原始時間序列中去除，得到僅包含趨勢部分和不規則部分的季節性修正時間序列圖如圖3所示。由于剔除了季節性因素的影響，因此根據圖3可知：2001年～2006年，該港口集裝箱吞吐量呈現緩慢上升趨勢，但吞吐量的增長情況并不穩定。2006年至2008年集裝箱吞吐量增長速度呈直線上升，在2009年集裝箱吞吐量下降，隨后至2014年又呈現出緩慢上升的趨勢，這主要是由于2008年全球金融危機全面爆發，沿海港口吞吐量下降所致[17]。

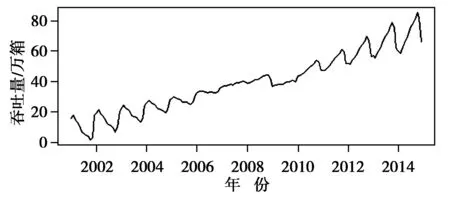
圖3　季節性修正時間序列圖Fig.3 Time sequence after seasonal adjustment

2.2港口集裝箱吞吐量時間序列建模與預測

為消除季節性和長期趨勢的影響，對時間序列作一階12步差分，最終得到的時間序列如圖4所示。差分后序列基本平穩。由于對原始時間序列數據做1階差分獲得了一個平穩時間序列，所以可以對時間序列使用ARIMA(p,d,q)模型，其中：p為自回歸模型的階數；d為差分階數，由上述內容可知，本文中d=1；q為滑動平均模型的階數。

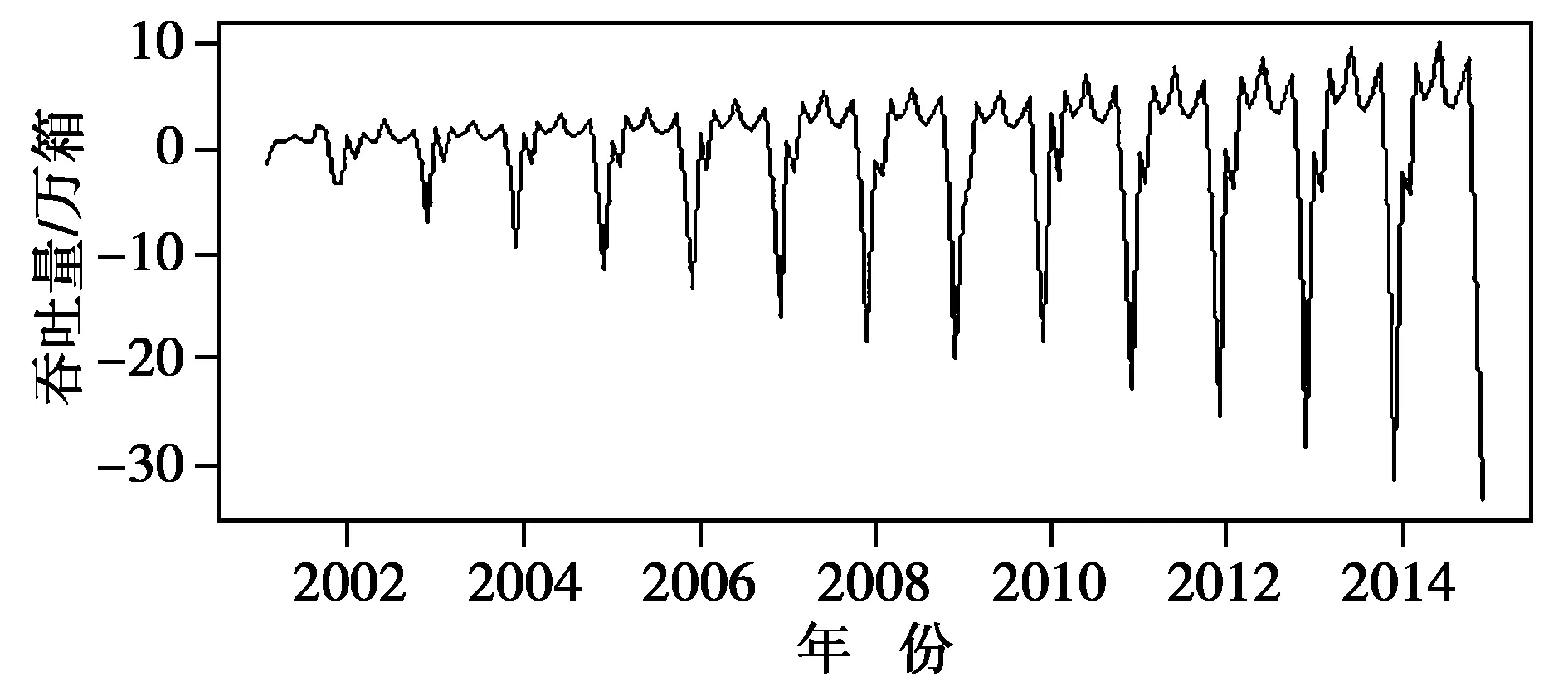
圖4　差分后的時間序列圖Fig.4 Time sequence after differential treatment

利用R軟件的程輯包‘forecast’中的arima函數，自動對非平穩時間序列進行適當差分，分析求解出適合時間序列分析的模型。輸入auto.arima()進行自動求解，最終輸出結果說明該模型適合采用ARIMA(2,1,1)模型，通過分析得出模型為：

(1-1.1559B+0.4945B2)(1-B)Xt=(1+0.8978B)εt。

(5)

應用該模型來預測未來十個月該港口集裝箱吞吐量的數據，得到結果見表1。表1反映了2015年1月～10月該港口集裝箱吞吐量預測值，并顯示了置信度為80%和95%時的置信區間。根據預測，2015年前十個月的吞吐量預計分別為：1月份44.087萬箱，2月份45.301萬箱，3月份53.267萬箱，4月份61.875萬箱，5月份67.885萬箱，6月份70.575萬箱，7月份70.713萬箱，8月份69.542萬箱，9月份68.120萬箱，10月份67.056萬箱。

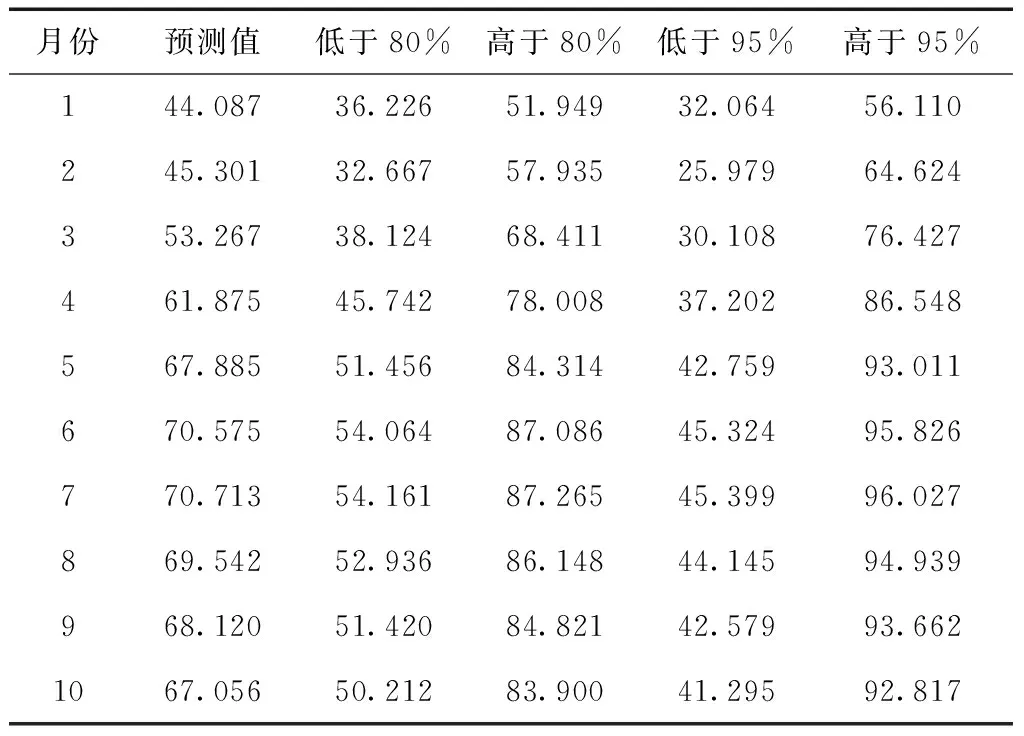
表1　2015年1月～10月預測值(萬箱)以及置信區間

預測值圖像如圖5所示，淺灰色陰影部分為80%預測區間，深灰色陰影部分為95%預測區間，陰影部分的線條表示預測值。

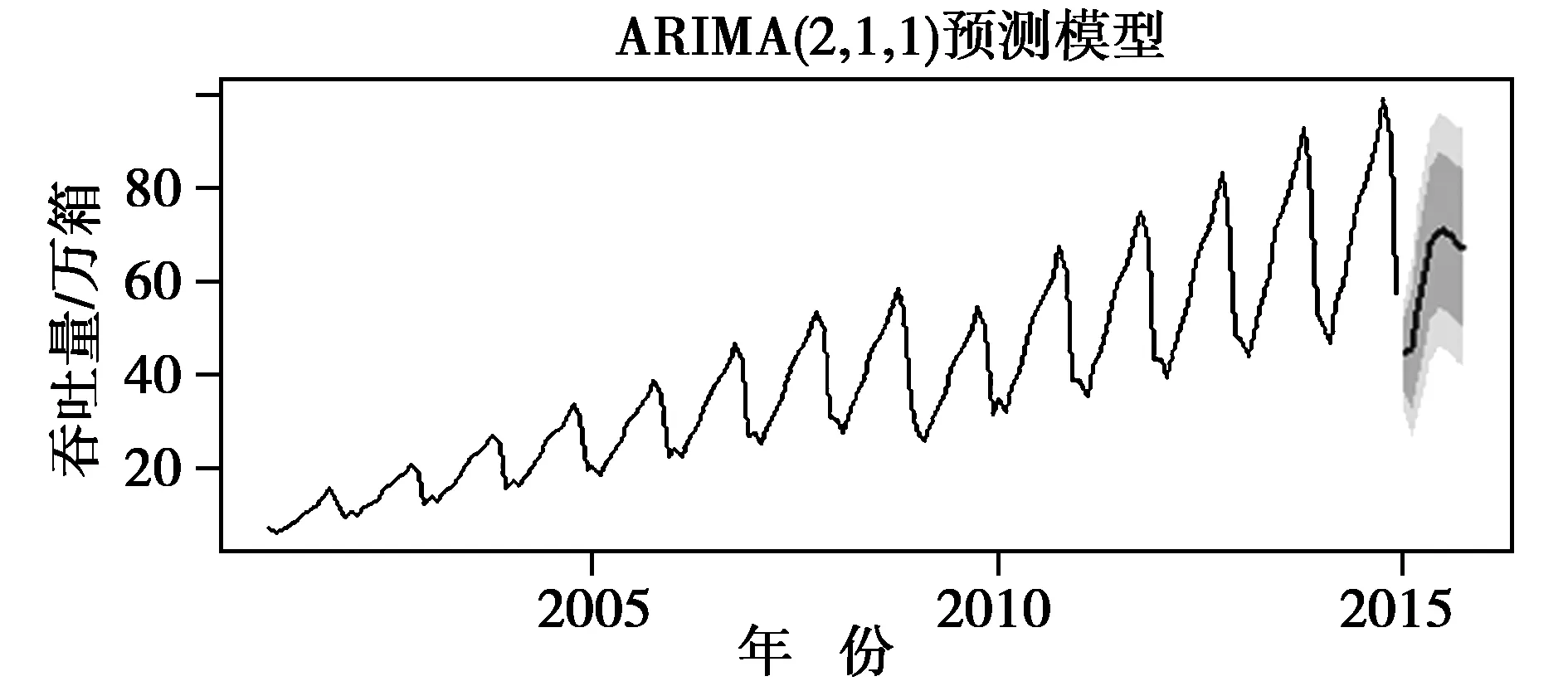
圖5　港口集裝箱吞吐量預測值圖像Fig.5 Predicted handling capacity of the port

對該港口吞吐量數據使用ARIMA(2，1，1)模型后所產生的預測誤差做自相關圖如圖6所示。由圖6可以看出，相關圖顯示出之后1～20階(lag1-20)中樣本自相關值都沒有超出置信邊界，而且Ljung-Box檢驗p-value < 2.2e-16，所以得到的模型可以提供非常合適的預測。

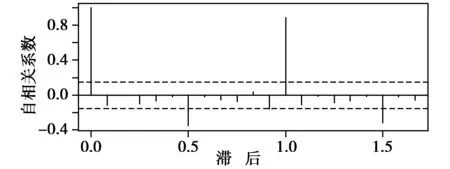
圖6　某港口集裝箱吞吐量預測誤差相關圖Fig.6 Correlation diagram of prediction error

2015年1月～10月該港口集裝箱吞吐量分別為46.721、47.014、56.335、60.982、68.452、73.146、75.178、70.015、69.574、68.739萬箱，與預測結果44.087、45.301、53.267、61.875、67.885、70.575、70.713、69.542、68.120、67.056萬箱相差甚微，在5%左右浮動，說明本模型對港口集裝箱吞吐量可以提供較準確的預測。

3　結束語

本文分析了2001～2014年某港口集裝箱吞吐量數據，通過時間序列分析，建立了集裝箱吞吐量的ARIMA預測模型，并且預測分析了2015年該港口前十個月集裝箱吞吐量，得到了以下結論：

(1)該港口集裝箱吞吐量總體呈現上升趨勢，2001～2003年這種趨勢不明顯，2003年以后隨著中國加入世貿組織，上升趨勢較為明顯。2009年前后該港口集裝箱吞吐量受金融危機的影響有下降趨勢，一段時間后隨著經濟的回暖逐漸恢復正常，至2014年又呈現出上升趨勢。

(2)該港口集裝箱吞吐量呈現一定的季節性變化，季節性因素最大值在十月，最小值在二月，一、二、三、四、五、十二月集裝箱吞吐量較少，標志著每年集裝箱吞吐量的峰值在十月，低谷在二月份。

(3)利用R軟件得到預測該港口2001年至2014年集裝箱吞吐量的預測模型ARIMA(2，1，1)模型為(1-1.1559b+0.4945b2)(1-B)Xt=(1+0.8978B)εt，并對模型進行檢驗，結果證明得到的模型可以很好的描述港口集裝箱吞吐量，從理論上證明了該港口集裝箱吞吐量的增長趨勢。

[1]葉峰，吳迎學.基于實現我國港口物流聯盟的探索[J].森林工程，2009，25(5)：89-91.

[2]Huang A，Qiao H，Wang S.Forecasting container throughputs with domain knowledge[J].Procedia Computer Science，2014，31：648-655.

[3]Huang A，Lai K K，Qiao H，et.al.An interval knowledge based forecasting paradigm for container throughput prediction[J].Procedia Computer Science，2015，55：1381-1389.

[4]Chen S H，Chen J.Forecasting container throughputs at ports using genetic programming[J].Expert Systems with Applications，2010，37(3)：2054-2058.

[5]翟希東.港口集裝箱吞吐量預測模型研究[D].大連：大連理工大學，2006.

[6]黃維忠.集裝箱吞吐量的動態預測研究[J].上海海運學院學報，2001，22(1)：45-48.

[7]江艦，王海燕，楊贊.集裝箱吞吐量及主要影響因素的計量經濟分析[J].大連海事大學學報，2007，33(1)：83-86.

[8]陳濤燾，高琴.港口集裝箱吞吐量影響因素研究[J].武漢理工大學學報，2008，30(6)：991-994.

[9]劉志杰，季令，葉玉玲，等.基于徑向基神經網絡的集裝箱吞吐量的組合預測[J].同濟大學學報，2007，35(6)：739-744.

[10]侯成琪，徐緒松.計量經濟學方法之時間序列分析[J].技術經濟，2010，29(8)：51-57.

[11]潘迪夫，劉輝，李燕飛.基于時間序列分析和卡爾曼濾波算法的風電場風速預測優化模型[J].電網技術，2008，32(7)：82-86.

[12]羅芳瓊，吳春梅.時間序列分析的理論與應用綜述[J].柳州師專學報，2009，24(3)：113-117.

[13]韓忠明，陳妮，樂嘉錦，等.面向熱點話題時間序列的有效聚類算法研究[J].計算機學報，2012，35(11)：2337-2347.

[14]錢愛玲，瞿彬彬，盧炎生，等.多時間序列關聯規則分析的論壇輿情趨勢預測[J].南京航空航天大學學報，2012，44(6)：904-910.

[15]楊娟麗，徐梅，王福林，等.基于BP神經網絡的時間序列預測問題研究[J].數學的實踐與認識，2013，43(4)：158-164.

[16]Aslanargun A，Mammadov M，Yazici B，et.al.Comparison of ARIMA，neural networks and hybrid models in time series：tourist arrival forecasting[J].Journal of Statistical Computation and Simulation，2006，77(1)：29-53.

[17]賈大山.金融危機對港口集裝箱發展的影響[A].全球經濟形勢變化與我國集裝箱運輸發展對策研討會論文集[C]，北京，2009：39-42.

Prediction of the Container Throughput in a PortBased on Time Sequence Analysis

Kong Linlin1，Liu Lan2，Xu Wenxiu1，Wu Jinzhuo1*

(1.College of Engineering and Technology，Northeast Forestry University，Harbin 150040；2.Hunan Institute of Technology，Hengyang 421002，Hunan Province)

Container transportation is one of the main modes of international transportation.Long-term monitoring port container throughput and predicting future trends are of importance to the port infrastructure construction，regional economic development and national strategy development.In this paper，aiming at the nonlinear characteristics of the factors affecting the complexity of port container throughput，the container throughput data in a port in China between January 2001 and December 2014 were investigated and statistical analysis software R was used to conduct time series analysis on the data.A reasonable model was put forward to describe the change of container throughput data，which was tested and optimized.The container throughput data after ten months was forecasted by using the model.Results showed that the prediction model after time series analysis can well describe the change of the port container throughput，therefore can provide reference for the optimal measures in different periods.

container throughput；time series analysis；forecast；model

2016-03-31

國家留學回國人員科技活動資助項目(人社廳函[2012]258號)

孔琳琳，碩士研究生。研究方向：森林工程。

吳金卓，博士，副教授。研究方向：森林工程，物流工程。E-mail：wujinzhuo1980@163.com

孔琳琳，劉瀾，許文秀，等.基于時間序列分析的港口集裝箱吞吐量預測分析[J].森林工程，2016，32(5)：106-110.

F 552

A

1001-005X(2016)05-0106-05