動力定位船舶偽逆法與混沌粒子群法相融合的推力分配算法研究
劉 明,華 亮,周 俊,戴 偉,邱愛兵
(南通大學 電氣工程學院,江蘇 南通 226019)
動力定位船舶偽逆法與混沌粒子群法相融合的推力分配算法研究
劉 明,華 亮,周 俊,戴 偉,邱愛兵
(南通大學 電氣工程學院,江蘇 南通 226019)
動力定位船舶一般都裝備冗余推進器,推力分配求解將直接影響最終定位的效果。針對偽逆法在推力分配中存在問題,提出一種把偽逆法和混沌粒子群法(CPSO)相融合的推力分配算法,該組合算法方便處理推力器各種限制條件,計算簡單,能兼顧船舶的能耗及操作性,解決奇點問題。最后以某挖泥船為例,仿真結果表明該推力分配算法具備一定的實用指導價值,能有效提高船舶的定位性能。
動力定位;粒子群算法;推力分配;偽逆法;混沌算子
Abstract: Dynamic positioning ships are generally equipped with redundant thrusters, and thrust allocation will directly affect the positioning performance. In this paper, fusion of pseudo inverse method and chaos particle swarm algorithm(CPSO) is designed in order to resolve the problem of thrust allocation with pseudo inverse method, the algorithm is simple and convenient to handle and calculate various constraints of thrust allocation, and both consumption and maneuverability are considered to solve the singularity problem. Finally, a dredger is taken as an example, and simulation results show that the algorithm has a certain practical guidance value, and that the dynamic performances of dynamic positioning ship are improved.
Keywords: dynamic positioning; particle swarm optimization; thrust allocation; pseudo inverse method; chaos operator
船舶動力定位系統主要由控制系統、測量系統和推力系統組成[1]。推力系統作為執行機構其運行性能直接影響定位效果,故良好的推力分配策略對提高定位精度、可靠性及降低能耗等具有很現實的意義。動力定位船舶一般都裝備冗余推進器,推力系統為過驅動系統,即控制器的輸出維數小于推進器控制量的維數。一方面冗余的推進系統提高了定位系統的可靠性;另一方面帶來如何獲得每個推進器輸出推力的最優方向和大小的問題。
過驅動系統的推力分配求解總體上屬于非線性優化問題,通常該類問題都轉化為在若干約束條件下求取目標函數最小值的優化問題,目標函數一般包括能耗、推力系統奇異性、推進器磨損、合力誤差和方位角變化速率等多重性能指標。常見求解推力分配問題的算法有直接分配法、序列二次規劃法、偽逆法[2-4]等等,此外隨著群智能優化算法(比如粒子群法[5-6]、蜂群算法、遺傳算法等等)的發展,國內外部分相關學者把該類算法用于求解推力分配問題進行了探討。其中偽逆算法是最簡單、最直接的推力分配算法,但該類算法本身主要考慮能耗,而忽視機械磨損、推進器本身限制等因素,通常導致奇點現象,故國內外一些專家對此算法進行了改進,文獻 [7]中針對981鉆井平臺,提出基于擴展推力的拉格朗日最小平方優化的顯性解,并在此基礎上,對推進器本身的推力大小、方位角及其變化率作了限制,獲得較好的定位性能。文獻 [4]在擴展推力能量最優分配基礎上,提出組合偏置思想并設計了自適應組合偏置策略,建立組合偏置推力分配算法,仿真表明該算法能有效提高船舶的動態性能。此外,群智能優化算法雖然在處理推力分配約束條件上具有計算簡單等優勢,但要在實際工程中應用,必須解決收斂性和實時性問題。
本文提出的偽逆法和混沌粒子群法(CPSO)相融合的推力分配策略實質是以帶權重系數的偽逆算法為基礎,運用CPSO算法進行權重系數尋優。CPSO算法是一種改進的粒子群算法,其設計以解決收斂性和實時性為目標,由于這里提出的算法以偽逆算法為基礎,一定程度上為解決收斂性和實時性問題提供了可行性的條件。最后以挖泥船仿真實例(該實例暫不考慮舵的因素)來驗證算法的可行性。
1 基于偽逆法的推力分配
1.1 船舶動力定位數學模型
對于具備動力定位系統的船舶,一般只研究船舶三個自由度上的運動控制,即艏搖、縱蕩和橫蕩,而忽略縱搖、垂蕩和橫搖三個自由度的運動控制。船舶三個自由度運動可以由下述向量進行描述:η=[x,y,ψ]T,υ=[u,v,r]T。其中η表示大地坐標系下船舶的位置和艏搖角度,υ表示隨船坐標系下船舶的縱蕩、橫蕩和艏搖速度。兩種坐標系相互轉換關系為[4]:
式中:R(ψ)為轉換矩陣。
動力定位船舶的低頻運動模型:
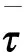
1.2 偽逆法推力分配
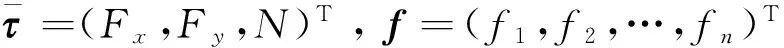
式中:(lxi,lyi),表示第i個推進器在船體坐標系中的位置,i=1,2,…,n。
為簡化推力方程的求解,S?rdalen引入了擴展推力fe,將方位角變化的推進器推力分解成縱蕩和橫蕩兩個相互正交的力:
此時,推力分配方程可以表示為:
以推進器推力平方和為目標函數,推力分配方程為約束條件構造拉格朗日函數[4]:
其中,λ為拉格朗日算子。根據拉格朗日極小值存在條件得:
綜上所述知,該方法求解推力分配時僅考慮推力分配方程約束條件和推力平方和目標函數,其它的約束條件和性能指標并未考慮,結果可能導致推進器在執行分配推力時由于本身條件約束使得不能按照需求值動作,機械磨損大,存在奇異點現象等問題。
2 偽逆法與CPSO相融合推力分配算法
2.1 推力分配布局情況
本文的仿真母型船布局情況如圖1所示,包括尾部兩個全回轉推進器和艏部兩個可正反轉的隧道推進器,各推進器坐標分別為(-64,-12),(-64,12),(66,0),(64,0)。由圖1可知其推力分配方程可表示為:
且偽逆法求解式中權值系數w-1為6×6正定對角陣。
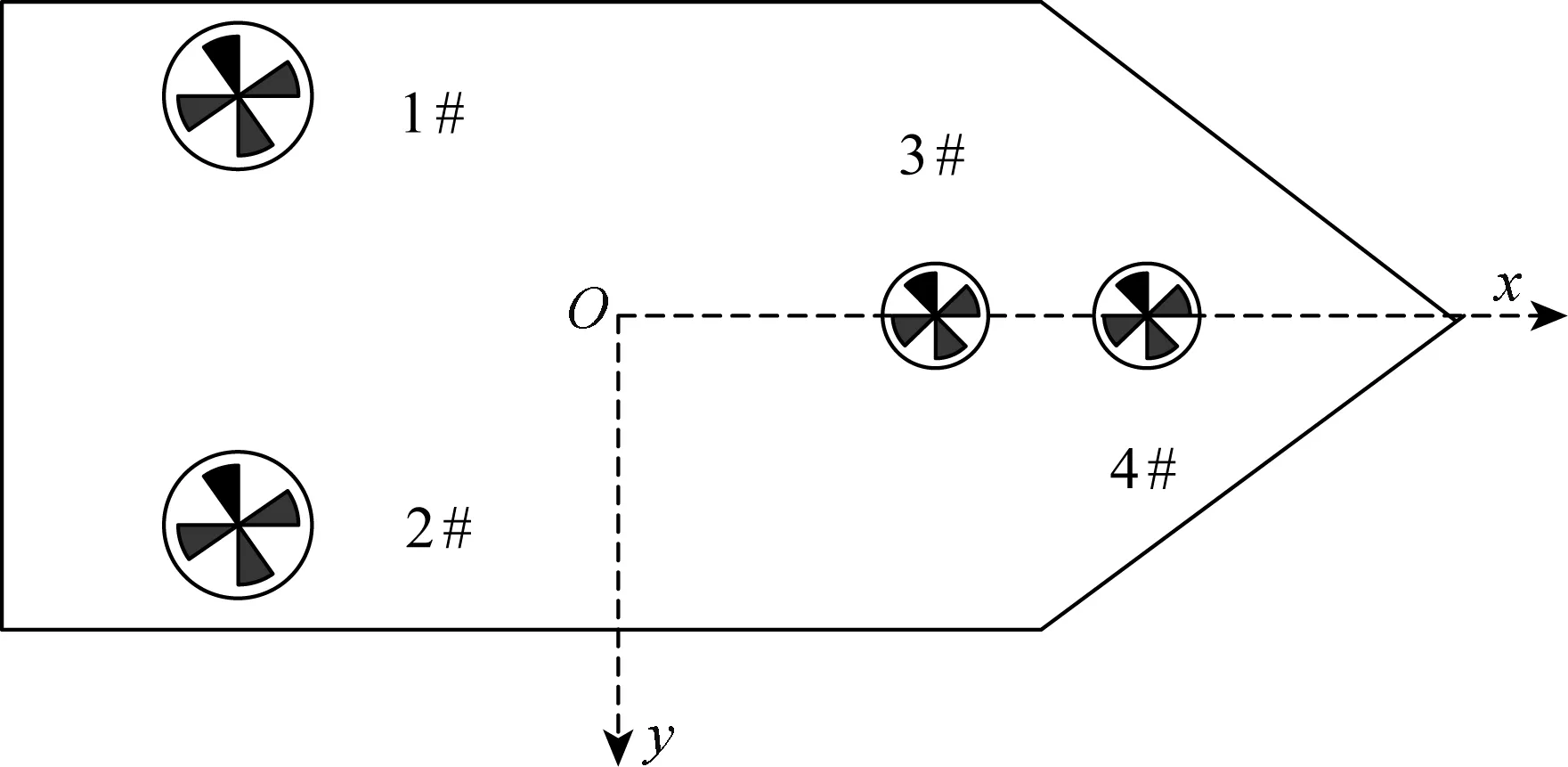
圖1 推進器布局示意Fig. 1 Schematic diagram of thruster layout
2.2 混沌算子及CPSO
混沌是一種普遍的非線性現象,行為復雜類似隨機,具有隨機性、遍歷性、規律性和敏感性。鑒于混沌的這些特性,利用混沌算子進行優化搜索比盲目無序的隨機搜索更具優越性,能夠避免演化算法陷入局部最優點,混沌優化算法是一種全局性的優化算法。
首先采用混沌序列初始化種群,可使粒子分布較均勻,粒子分散性較好,為全局搜索多樣性奠定基礎[8];其次,在尋優過程中,防止粒子早熟停滯現象出現,利用有效判斷方法,發現早熟跡象,利用混沌序列隨機產生粒子替代對應粒子,使其跳出局部最優。
混沌映射一般有如下幾種形式:二維cat映射;logistic映射;tent映射等等。其中,logistic映射方程如式(13)所示:
式中:xn是變量x在第n步迭代時數值,其中初始值x0∈(0,1),0.25,0.5和0.75除外;u是混沌映射的控制參數,當u=4時,logistic映射方程進入完全混沌狀態[9]。
目前PSO算法及相關改進PSO算法中粒子初始化基本采用隨機方式產生,這也是每次搜索結果不一致,甚至差別較大的最主要原因之一。研究表明參數搜索空間和粒子初始化分散性對搜索結果產生較大影響。CPSO算法相對標準粒子群算法在粒子初始化方面進行改進,其粒子初始化為利用混沌算子進行粒子初始化和定目標相結合的一種方式,根據現有方法(如Ziegler Nichols法)和專家經驗進行參數搜索空間的初步選定,混沌算子產生粒子,使得該算法具有大范圍的尋優能力。
2.3 偽逆法與CPSO相融合優化算法
1) 算法運行機制多樣化
為滿足算法的工程實用性,采取多樣化的算法運行機制。①粒子初始化種群大小采取M+1模式,即除了采用混沌算子進行M(一般取奇數)個種群隨機初始化之外,偽逆法中固定權值系數數值作為初始種群之一,該模式有利于獲得能耗最低可行性解。②粒子速度更新多樣化,即一部分粒子采用標準粒子群更新模式,一部分粒子采取定目標經驗更新模式,多樣化模式使得算法即具備全局尋優能力,又可以具有較高的收斂速率。③算法運行終止條件“四關”制:當前系統推力指令與上一時刻相同時,則各推進器推力輸出按照上一時刻分配結果執行;如推力指令不相同,首先計算粒子初始化中“1”模式的粒子性能指標,判別是否滿足推力分配需求,如滿足則結束運行;在每次迭代過程中判別是否有滿足條件的粒子存在,如有滿足則結束運行;迭代次數是否達到最大值,如達到則結束運行,該終止條件模式是算法降低運行時間的關鍵之一。④種群逐代遞減策略,按照一定淘汰規律逐步降低種群數,降低推力分配求解時間。
2) 約束條件和目標函數
推力分配參數優化是求目標函數的極小值問題,通常優化的目標包括推進器的磨損、能耗、系統的奇異結構等,故目標函數可表示為[7]:
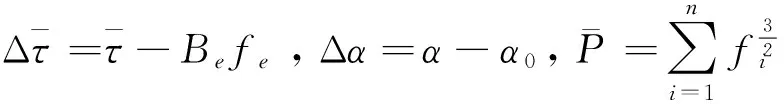
約束條件為:
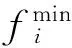
3) 算法流程
Step1判別當前系統推力指令與上一時刻是否相同,如相同則各推進器推力輸出按照上一時刻分配結果執行,終止算法運行,否則執行Step2。
Step2 初始化”1”模式粒子,其值為對角全為0.5的對角陣,采用偽逆法求解推力分配,判別是否滿足推力分配需求條件,如滿足則終止算法運行,輸出推力分配結果,否則執行Step3。
Step3初始化算法參數。初始化粒子種群大小M(一般取20~40),搜索空間維數D=6,迭代次數n,搜索空間范圍[0,1],飛行速度(Vi=(vi1,vi2,…,viD))的范圍Vmin,Vmax(取值可以根據搜索空間范圍進行初步選定),學習因子C1和C2(一般取值為2),權值w1,權值對角矩陣w2,權值矩陣w3, logistic混沌映射的控制參數,推進器約束參數等。
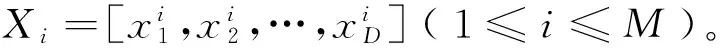
Step5 根據式(14)適應度評價函數計算粒子群中每個粒子的適應度值。
Step6 將每個粒子當前適應度值與個體極值pBest(記為pi=(pi1,pi2,…,piD))進行比較,若當前適應度值小于個體極值,則將其值作為個體極值,找出當前適應度值中最小值,將其與整個種群最優解位置gBest(記為pg=(pg1,pg2,…,pgD))比較,若其值小于gBest,則將其值作為gBest。判別是否滿足推力分配需求條件,如滿足則終止算法運行,輸出推力分配結果,否則執行Step7。
Step7 采用標準粒子群更新的粒子,更新方法如下:
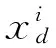
粒子的速度約束如下:
更新每個粒子的位置,更新公式可以表示如下:
粒子的位置約束如下:
式(18)~(21)中,1≤d≤D。
采取定目標經驗更新的粒子,其方法為:粒子(權重系數)與推力分配結果間存在一定關系,即某個權重系數對推力分配結果的影響趨勢是已知的,故可根據當前推力分配結果,按照一定規律修改對應的權重系數值。
Step8根據優勝劣汰機制,按照一定模式遞減粒子種群數。
Step9 判斷是否達到最大迭代次數或優化的終止條件,如達到則此次循環終止,輸出最優搜索結果,否則返回Step5 。
3 算法實例仿真
為驗證本文提出的推力分配算法,以某挖泥船為對象進行仿真分析,其推進器布置如圖1所示。該船主要技術數據如表1所示。
船舶初始位置為東0 m北0 m,初始艏向為0°,目標位置為東6 m北8 m,目標艏向為17.2°,采用PID控制策略對挖泥船進行運動控制,1 s為一個控制節拍,推力分配分別采用文中提出的融合算法和偽逆法進行仿真,仿真結果如圖2所示。

表1 某挖泥船的主要技術參數Tab. 1 Main technical parameters of a dredger
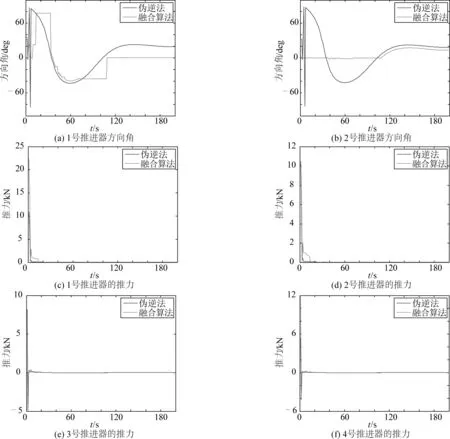
圖2 推進器的方向角和推力仿真結果Fig. 2 The result of azimuth angles and thrust force of thrusters
由圖2(a)和圖2(b)可以看出,1號推進器和2號推進器采用本文提出的融合算法,其方向角變化幅度總體上比采用偽逆法要小的多,特別是2號推進器的方向角變化幅度很小,有利于減少推進器的機械磨損,此外采用偽逆法時1號推進器和2號推進器的方向角變化幾乎一致,而采用文中提出的融合算法時1號推進器和2號推進器的方向角變化不一致性較大,這樣有利于提高船舶的操縱性,避免推進器系統奇異結構。
由圖2(c)~2(f)可以看出,兩種方法推進器消耗的能量差別不大。其中圖2(c)和圖2(f)顯示融合算法消耗的能量略大于采用偽逆法,圖2(d)和圖2(e)顯示融合算法消耗的能量略小于采用偽逆法,故文中提出的融合算法并不需要以較大的能量消耗換取船舶的操作性。
綜上所述可知,文中提出的融合算法能夠方便處理推力器各種限制條件,計算簡單,能兼顧船舶的能耗及操作性,解決奇點問題。
4 結 語
針對動力定位系統中推力分配問題,把偽逆法和CPSO算法進行融合,設計了融合算法的推力分配策略。通過挖泥船的仿真實驗,驗證了該算法的可行性,雖然該算法較偽逆法相對耗時,但該算法在兼顧能量消耗的同時,能有效的降低推進器的磨損,解決推進器系統奇異結構問題,推力分配結果合理,對實際工程運用具有一定理論指導意義。
[1] 王欽若,楊娜,葉寶玉,等.船舶動力定位系統推力分配策略研究[J].控制工程,2013,20(1):30-33. (WANG Qinruo, YANG Na, YE Baoyu, et al. Research on thrust allocation of ship dynamic positioning system[J].Control Engineering of China, 2013,20(1):30-33. (in Chinese))
[2] 王瑩,諶棟梁,謝穎,等.基于構造矩陣零空間的動力定位系統推力分配方法[J].海洋工程,2013,31(4):30-36.(WANG Ying, CHEN Dongliang, XIE Ying, et al. A thrust allocation method for dynamic positioning system based on the null space of configuration matrix[J].The Ocean Engineering, 2013,31(4): 30-36. (in Chinese))
[3] 梁海志,歐進萍.半潛式平臺動力定位系統控制力動態約束分配法[J]. 海洋工程,2012,30(1):33-39. ( LIANG Haizhi,OU Jinping. Dynamic positioning system thrust allocation algorithm with dynamical thrust constrains of semi-submersible platform [J]. The Ocean Engineering, 2012,30(1):33-39. (in Chinese))
[4] 施小成,魏玉石,寧繼鵬, 等.基于能量最優的組合偏置推力分配算法研究[J].中國造船,2012,53(2):96-104. (SHI Xiaocheng, WEI Yushi, NING Jipeng, et al.Research on group biasing thrust allocation algorithm based on power optimization[J]. Ship Building of China, 2012,53(2):96-104. (in Chinese))
[5] LI Mingwei, KANG Haigui, ZHOU Pengfei, et al. Hybrid optimization algorithm based on chaos,cloud and particle swarm optimization algorithm[J]. Journal of Systems Engineering and Electronics, 2013, 24 (2):324-334 .
[6] MENHAS M I, FEI Minrui, WANG Ling, et al. Adaptive mutation based probability binary pso for control of ball mill pulverizing system[J]. Journal of System Simulation, 2011, 23(8): 1568-1574.
[7] 王芳,潘再生,萬磊,等.深水鉆井平臺動力定位的推力分配研究[J].船舶力學,2013,17(1-2):19-28. (WANG Fang, PAN Zaisheng, WAN Lei, et al. Optimal thrust allocation for a dynamically positioned deepwater drilling rig[J].Journal of Ship Mechanics, 2013,17(1-2):19-28. (in Chinese))
[8] 朱海梅,吳永萍. 一種高速收斂粒子群優化算法[J]. 控制與決策, 2010, 25(1):20-24. (ZHU Haimei, WU Yongping. A pso algorithm with high speed convergence[J].Control and Decision, 2010, 25(1): 20-24 (in Chinese))
[9] LI Mengshan, HUANG Xingyuan, LIU Hesheng, et al. Prediction of the gas solubility in polymers by a radial basis function neural network based on chaotic self-adaptive particle swarm optimization and a clustering method[J]. Journal of Applied Polymer Science, 2013, 130(5): 3825-3832.
Research on dynamic positioning thrust allocation algorithm based on pseudo inverse method and CPSO algorithm
LIU Ming, HUA Liang, ZHOU Jun, DAI Wei, QIU Aibing
(School of Electrical Engineering, Nantong University, Nantong 226019, China)
1005-9865(2016)04-0100-07
U664
A
10.16483/j.issn.1005-9865.2016.04.014
2015-05-22
國家自然科學基金(61104028 );南通市科技計劃項目(BK2014075)
劉 明(1981-),男,江蘇宿遷人,講師,從事船舶動力定位智能控制方向研究。E-mail:liumingsongliuming@126.com

