多目標速度估計的分布式MIMO雷達資源分配算法

胡捍英 孫 揚 鄭娜娥

?

多目標速度估計的分布式MIMO雷達資源分配算法

胡捍英 孫 揚*鄭娜娥

(解放軍信息工程大學導航與空天目標工程學院 鄭州 450001)

為了提高分布式MIMO雷達的多目標速度估計精度，該文分析了發射功率和信號有效時寬對估計精度的影響，進而提出一種將兩者聯合優化的資源分配算法。首先，以最小化目標速度估計的克拉美羅界(CRLB)最大值為目標函數，建立了包含發射功率和信號有效時寬兩個優化變量的優化模型，然后采用連續參數凸估計(Sequential Parametric Convex Approximation, SPCA)算法對這個非凸的優化模型進行求解。最后，仿真結果表明利用所提算法進行資源分配能明顯提高目標速度的估計精度。此外，仿真結果表明信號有效時寬對目標速度估計精度的影響大于發射功率。

分布式MIMO雷達；多目標速度估計；功率分配；信號有效時寬分配

1 引言

多輸入多輸出(MIMO)雷達[1,2]是采用多個發射陣元發送定制波形信號，并采用多個接收陣元對回波進行某種聯合處理的雷達系統，已成為了新體制雷達研究的熱點。理論上，MIMO雷達系統所包含的陣元數目越多，發射功率越大，目標的參數估計精度就越高[3]。但是在實際應用中，由于MIMO 雷達是一種多傳感器跟蹤系統，數據融合[4]是進行信號處理的基本步驟。因此陣元數目越多，傳輸量就越大，融合中心的計算復雜度也會越高。另一方面，對于特定的應用場景，例如軍事對抗中如何降低雷達截獲率，以及在總能量有限的情況下如何達到更好性能等，也對系統的資源分配提出了具體的要求。因此，如何合理地分配MIMO雷達系統的有限資源，以獲得更好的系統性能，正越來越多地受到國內外學者的關注。

MIMO雷達系統的資源分配主要可以分為兩類[5]，一類是基于系統結構的分配方式，如陣元的數目和布置；另一類是基于發射參數的設置，如發射功率，帶寬和信號有效時寬等。針對系統結構的資源分配問題，文獻[6]提出了一種基于陣元子集選取優化的定位算法，包含了兩種優化模型：一種是在達到要求的定位精度下，使用最少數目的陣元；另一種是挑選給定數目的陣元，以達到最好的定位精度。文獻[7]提出了一種基于陣元聚類分配的多目標定位算法，在滿足各個目標的定位精度需求的前提下，使陣元數最少。而針對于發射參數的配置，文獻[8,9]基于分布式MIMO雷達平臺，以目標定位誤差的CRLB[10]作為目標函數，通過分配功率資源使目標的定位精度更高。文獻[11]在其基礎上考慮了發射信號正交時帶寬對目標定位精度的影響，提出了功率和帶寬聯合分配的算法，進一步優化了定位精度。文獻[12]將非合作對策論思想[13]和功率分配結合起來，在達到給定目標定位精度的條件下使MIMO雷達發射總功率最小。針對系統結構和發射參數聯合優化的問題，文獻[14]通過優化陣元位置和功率分配來提高MIMO雷達的目標探測性能。文獻[15]將陣元子集選取和功率分配聯合優化來提高MIMO雷達的目標定位精度。

上述文獻提出的資源分配算法提高了MIMO雷達的參數估計性能，但是仍然存在一些可以改進的地方：(1)僅針對固定目標的位置進行資源分配，沒有考慮運動目標的速度估計性能；(2)針對發射參數的配置時，文獻[8-12]均使用所有發射陣元，會導致資源浪費，而且冗余的陣元還會增加融合中心的計算復雜度；(3)在發射信號正交的情況下，速度估計精度不僅與發射功率、陣元有關，還與信號有效時寬有一定的關系[5,16]，因此應當考慮它對速度估計精度的影響。

出于上述考慮，本文提出了一種多目標速度估計的分布式MIMO雷達資源分配算法。首先，分析了影響目標速度估計精度的因素，描述了3種資源分配問題，即發射功率優化分配，信號有效時寬優化分配以及兩者聯合優化分配；其次以最小化目標速度估計的均方誤差下界[16](CRLB)的最大值為目標函數，建立了包含發射功率和信號有效時寬兩個優化變量的資源分配優化模型；然后采用連續參數凸估計(Sequential Parametric Convex Approximation, SPCA)[17]算法對該非凸問題進行求解，得到功率和信號有效時寬的分配結果。最后，采用最大似然估計求得目標速度的均方根誤差(MSE)，仿真實驗結果驗證了本文算法的有效性。

2 信號模型

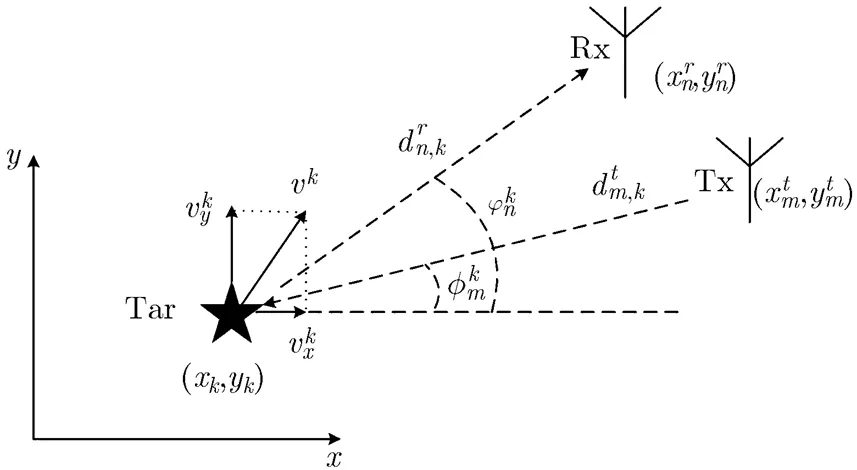
圖1 發射和接收陣元相對目標及其運動方向的位置示意圖

3 資源分配優化算法

3.1構造目標函數

考慮到CRLB在高信噪比條件下與參數的無偏估計十分接近，并且它對于代數運算比較方便，所以本文的資源分配優化模型選取其作為目標函數。定義第個目標速度估計的CRLB矩陣為，其對角元素之和為的均方誤差(MSE)的最低界限，即該矩陣的跡滿足。考慮MIMO雷達在發射信號完全正交的情況下，分布式MIMO雷達的單個目標的速度估計的CRLB可由文獻[16]推導得到

由式(3)的定義可知，目標速度估計的CRLB與發射功率，信號有效時寬，陣元的位置和數目，目標的位置和復反射系數，路徑衰減有關。記個目標的速度估計的CRLB為一個維的矢量，我們將其中速度估計誤差最大者作為目標函數，目標函數可以描述為

3.2優化模型的建立和求解

為了分析發射功率和信號有效時寬對目標速度的估計精度產生的影響，本節首先描述了發射功率與信號有效時寬聯合優化分配問題，因為單一的功率分配或者信號有效時寬分配均為聯合優化問題在不同情況下的特例。

為了簡便求解的過程，下面我們考慮將上述資源分配問題寫成統一的數學形式。首先由的定義可知，容易證明對于任意常數,。然后對于聯合優化問題，其最優解必定會滿足，其中表示功率矢量和信號有效時寬矢量的第個分量。由此可以將其簡化為僅對功率矢量的優化，求得后再求。注意到對于單一種類的資源優化問題而言，特定的和的值不會對最終的解產生實質影響，不妨分別假設和。

通過上述的推導，上述資源分配問題的目標函數和約束條件已經很相似，所以引入統一的目標函數：

則上述資源分配問題可以用統一優化模型描述：

容易得到發射功率優化分配，信號有效時寬優化分配和兩者聯合優化分配的解分別為

該優化模型求解最大值的過程出現在目標函數中，計算過程比較繁雜，所以考慮將其放在約束條件中，以簡便計算。不妨設，其中為常數，優化模型化為

式(10)是我們要求解的最終形式，對其分析可知其目標函數是一個線性函數，約束條件中第1個為多項式，第2個為線性約束。若多項式為凸函數，則其符合凸優化求解的條件，但是這點僅僅在取一些特殊值的時候才成立。所以需要利用非凸優化的方法求解，但這種方法往往無法得到全局最優解，而且這種方法的復雜度會隨著問題維數的增加而呈指數型增加。一種可以考慮的方法是利用SPCA算法得到近似解，該算法可以保證收斂到局部最優解[17]。根據SPCA算法，首先將式(10)中的非凸的約束條件分解成為一個凸函數和凹函數的和，即將矩陣分解成一個非負定矩陣和一個非正定矩陣。然后考慮將第2個等式約束條件松弛為，它也是一個凸函數和一個凹函數的和。

分析可知式(12)的可行域是凸的，而且它的約束條件是由式(11)泰勒展開而得到的，所以它的可行域是式(11)可行域的子集，所以它的解自然也是式(10)的解。得到該解后，由上述分析可知其為的條件下式(9)的特殊解，而式(9)與式(7)的解也只相差一個縮放因子。定義由式(12)的解通過縮放恢復得到式(7)的解的因子為，下面我們求解這個縮放因子。首先注意到對于式(7)，它在解處一定滿足，同時解滿足，由此可得到：

3.3 算法流程

步驟 2 運用凸優化方法求解式(12)中的優化問題，得到第次迭代的解，并將其作為第迭代過程中凹函數和線性化的起始點。

步驟 3 跳轉步驟2，直到連續兩次得到的目標函數沒有得到進一步優化時，將最后一次迭代的作為式(12)最終的解。然后根據式(14)就可以得到發射功率和信號有效時寬的優化分配結果，最后根據分配結果調節各個發射陣元的發射參數，對目標速度進行估計。

4 仿真結果及分析

場景1(固定布陣) 陣元和目標的位置關系示意圖如圖2所示，其位置分別為(單位為)

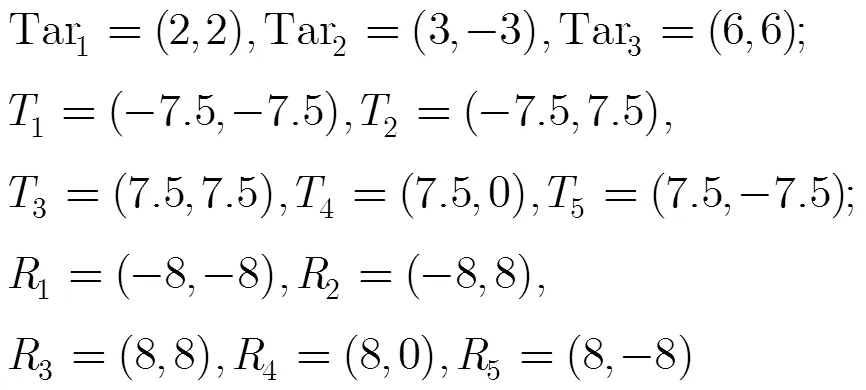
然后由資源分配算法得到各個發射陣元的資源分配情況如圖3所示。

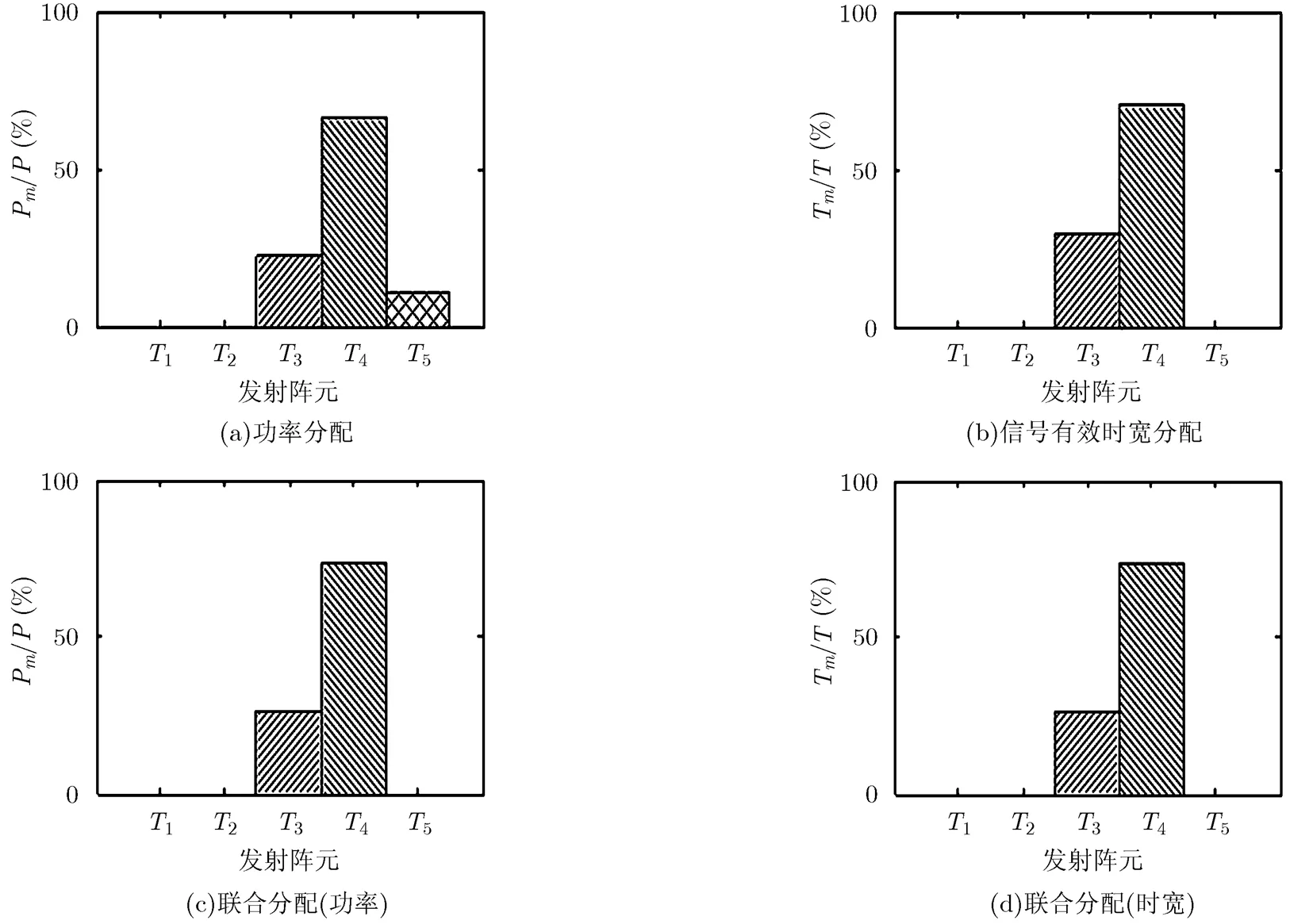
圖3 資源分配結果

由于目標的復反射系數相同，所以陣元和目標的距離成為資源分配的決定因素，由圖2可知發射陣元距離3個目標距離更近。分析圖3可知，功率分配策略將發射功率分配給了發射陣元，信號有效時寬分配策略和聯合分配策略則將資源分配給了發射陣元，證明了本文算法能夠將資源優先分配給那些對目標速度估計精度貢獻比較大的陣元，提高資源利用率，同時更少的陣元數目也可以降低融合中心的處理難度。另外，信號有效時寬分配和聯合分配比功率分配策略需要的陣元數目更少。

場景2(隨機布陣) 因為本文提出的資源分配算法與陣元的位置有關，為了避免實驗結果的偶然性，采用蒙特卡洛方法仿真，仿真次數設為1000。每次仿真中發射陣元和接收陣元，以及目標隨機分布在的區域內，服從均勻分布。首先通過仿真對不同分配策略下的陣元數目情況進行分析。在相同的信噪比下統計1000次仿真實驗中陣元選取的結果，仿真結果如圖4和表1所示。

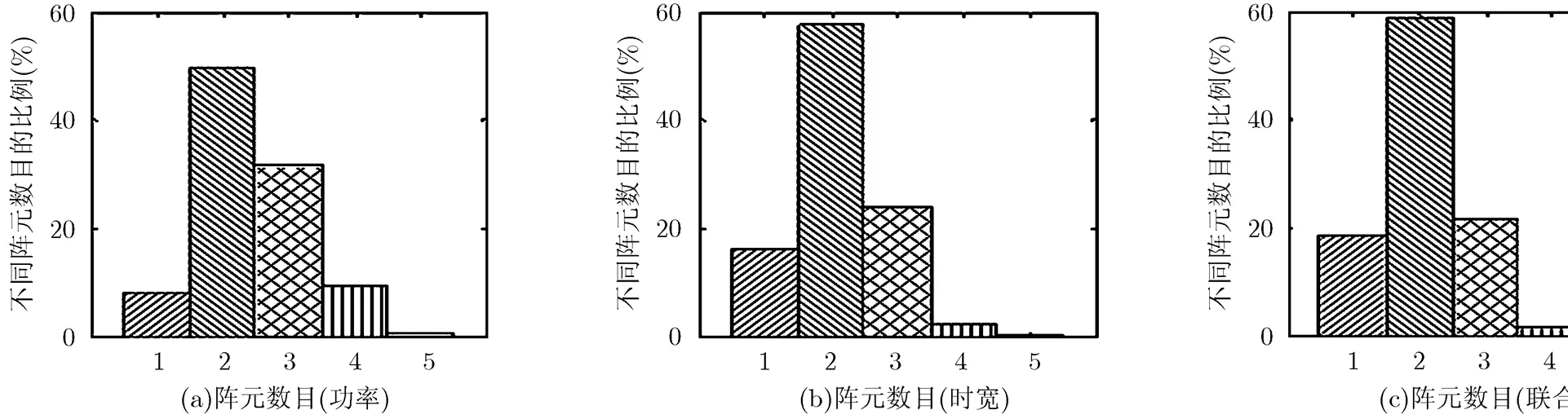
圖4 不同資源分配策略下的最優陣元數目選取情況

表1 不同資源分配策略下的最優陣元數目選取情況

由圖4和表1可知，3種資源分配策略的共同點是將資源分配給兩個發射陣元的情況所占比例最大，區別在于功率分配策略使用的發射陣元數目只需一個和大于兩個的情況所占比例分別為和，而信號有效時寬這兩種情況所占比例分別為和左右，聯合分配策略這兩種情況所占比例分別為和左右。表明聯合分配策略需要的陣元數目最少，信號有效時寬分配次之，而功率分配需要最多的陣元。

然后仿真了在不同的信噪比下目標速度的CRLB，如圖5所示。對圖中的每一個信噪比取值點，取1000次仿真得到的CRLB的平均值。另外，為了進一步對比分析本文算法的性能，該節還利用文獻[6]的極小化陣元數目的算法得到目標速度的CRLB，該算法是挑選一定數目的陣元，達到最好的參數估計精度。

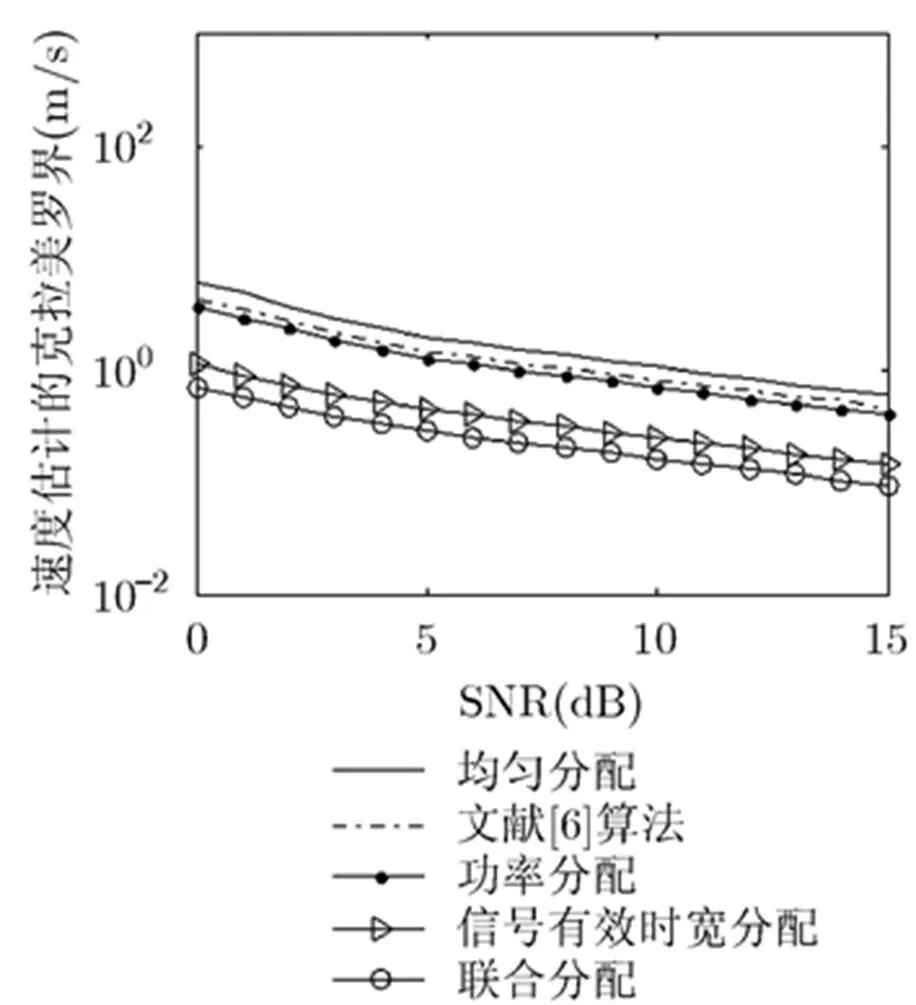
圖5 不同資源分配下速度估計的CRLB

圖5描述了4種資源分配策略下3個目標中速度估計誤差最大的CRLB隨著信噪比增大的變化趨勢，它們分別為：發射功率和信號有效時寬均勻分配，文獻[6]的算法，發射功率分配，信號有效時寬分配和聯合分配。由圖可知，聯合分配效果最好，而均勻分配效果最差，信號有效時寬分配表現次優，發射功率分配優于文獻[6]的算法，其中后者僅僅優于均勻分配。信號有效時寬分配要優于功率分配是因為信號有效時寬其在目標函數中是一個二次項形式，而發射功率則為一次項形式，所以前者對速度估計精度的影響比后者更大。另外，圖5表明本文算法對目標速度估計性能的提高要優于文獻[6]中的算法，這是因為本文算法不僅僅選取了位置更好的陣元，同時還在選取的陣元上進行合理的資源分配，進一步提高了目標速度的估計精度。它們的共同趨勢是CRLB隨著相干信噪比的增大而減小。

最后為了驗證基于CRLB的仿真結果的正確性，下面求得該MIMO 雷達系統對應的目標速度最大似然估計的均方誤差(MSE)。最大似然估計被證明是漸近最優的方法，在本文研究的問題中，因為均為1，目標速度的最大似然估計[16]為

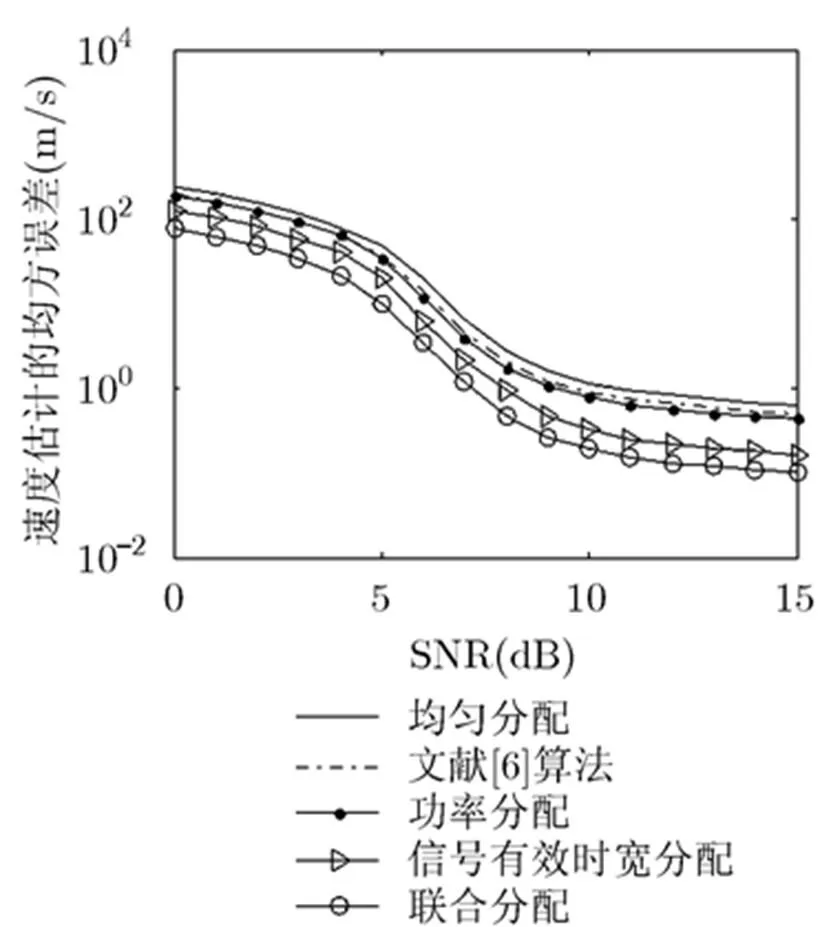
圖6 不同資源分配下速度估計的MSE

由于本文算法的目標函數是針對多目標中最差的目標速度估計精度進行優化，因此，嚴格意義上說是“保守”地提高了估計精度。為了進一步分析該算法對于其余目標的速度估計精度的影響，該節仿真了在不同的信噪比下其余目標速度的CRLB和MSE，其中最優的目標速度估計的仿真結果如圖7和圖8所示，次優的目標速度估計的仿真結果如圖9和圖10所示。

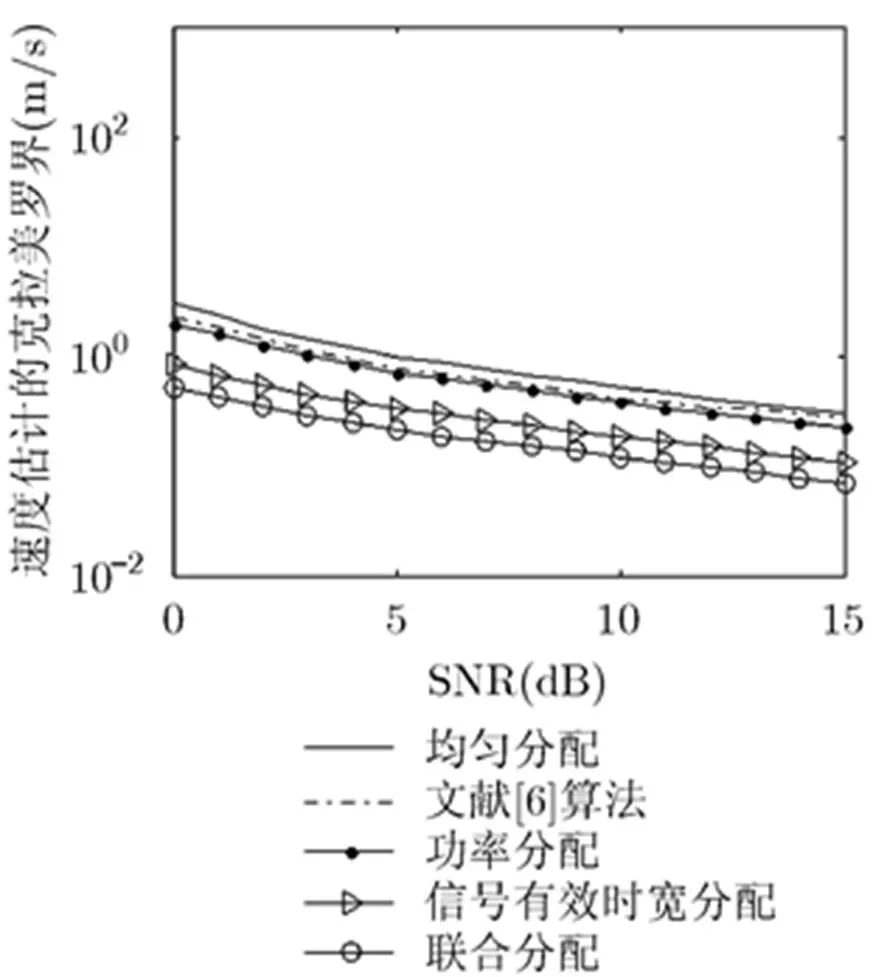
圖7 不同資源分配下最優目標速度的CRLB

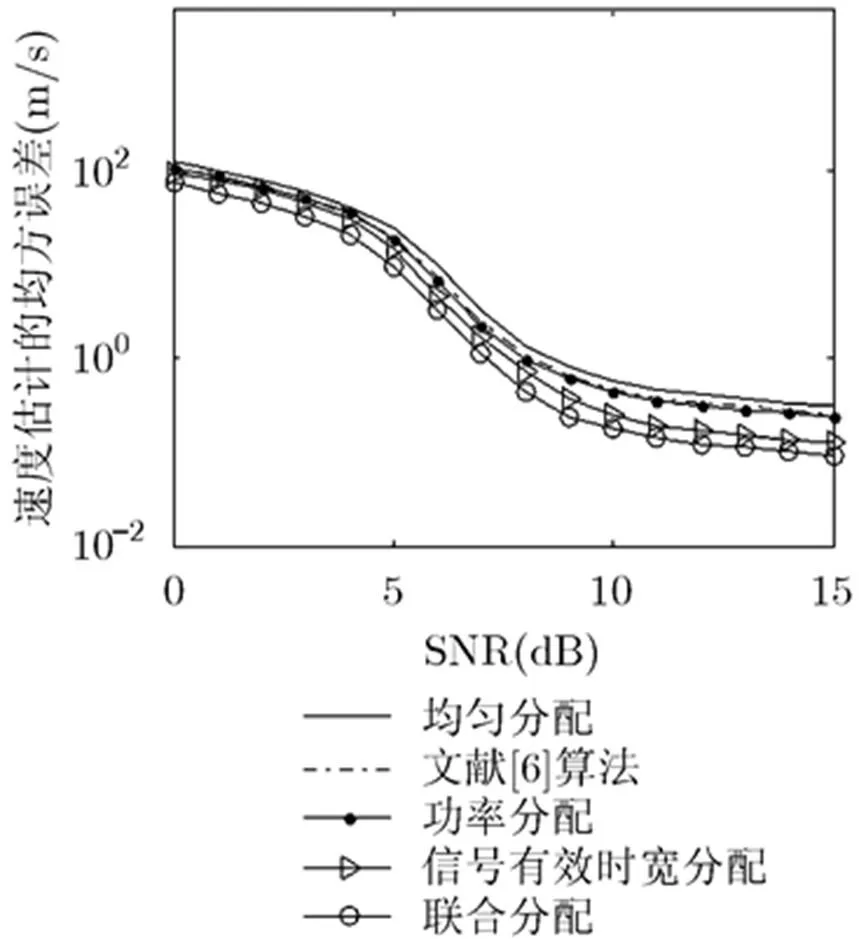
圖8 不同資源分配下最優目標速度的MSE

圖9 不同資源分配下次優目標速度的CRLB

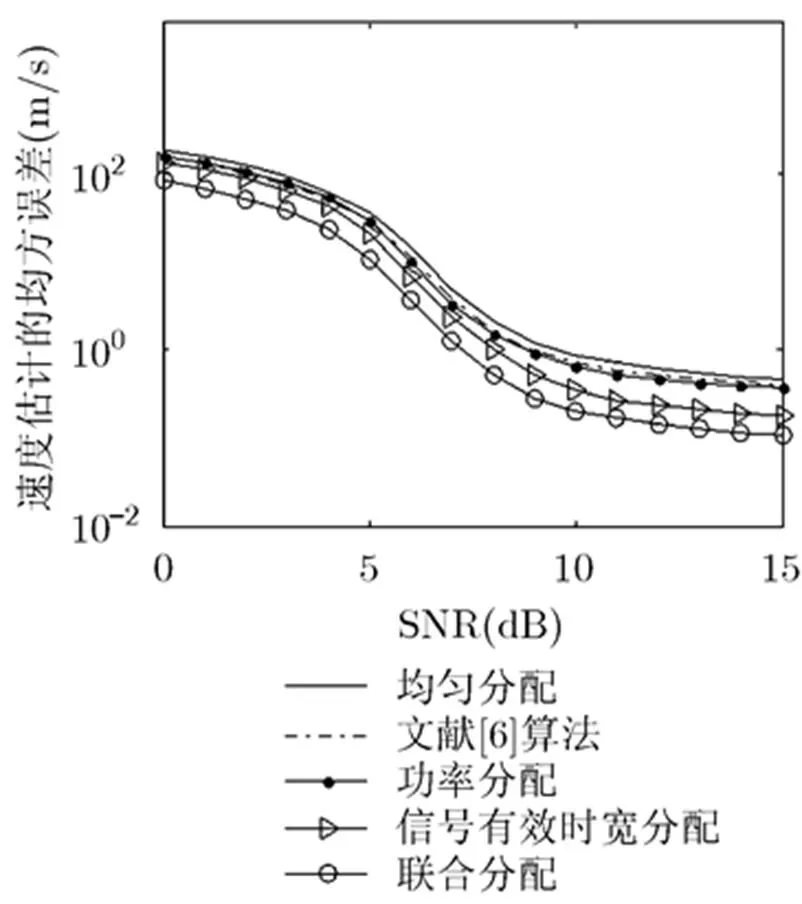
圖10 不同資源分配下次優目標速度的MSE

由圖7至圖10可知，本文提出的算法也能提高其他目標的速度估計精度。但分析其與圖5和圖6的區別可知，最優目標和次優目標的速度估計精度的優化程度比目標函數的更低，這是因為本文算法是針對最差的目標速度估計精度進行資源的優化分配。

5 結束語

本文在分布式MIMO雷達平臺下，針對多目標的速度估計優化問題，分析了發射功率和信號有效時寬對估計精度產生的影響，進而提出了一種將兩者聯合的資源分配算法，在系統資源有限的情況下進一步提高目標速度的估計精度。仿真結果表明，信號有效時寬比發射功率對目標速度估計精度的影響更大，而且聯合分配算法與資源均勻分配或者僅僅單獨分配其中一種資源相比，其性能是最優的。由于本文只對目標速度估計進行研究，因此考慮同時提高目標位置和速度的估計精度時，必須考慮信號帶寬和信號有效時寬的相互影響。這種情況下如何合理分配系統資源，將是下一步的重點研究工作。

參考文獻

[1] HAIMOVICH A, BLUM R, and CIMINI L. MIMO radar with widely separated antennas[J]., 2008, 25(1): 116-129.doi: 10.1109/MSP.2008. 4408448.

[2] DIONYSIOS S K and ATHINA P P. Matrix completion in collocated MIMO radar: recoverability, bounds & theoretical guarantees[J]., 2014, 62(2): 309-321.doi: 10.1109/TSP.2013.2287673.

[3] VAN T H L. Detection, Estimation, and Modulation Theory [M]. New York, John Wiley & Sons, 1971: 275-352.

[4] GODRICH H, CHIRIAC V, HAIMOVICH A,. Target tracking in MIMO radar systems: techniques and performance analysis[C]. Proceedings of the IEEE Radar Conference, Virginia, 2010: 1111-1116.doi: 10.1109/RADAR. 2010.5494453.

[5] 嚴俊坤, 糾博, 劉宏偉, 等. 一種針對多目標跟蹤的多基雷達系統聚類與功率聯合分配算法[J]. 電子與信息學報, 2013, 35(8): 1875-1881. doi: 10.3724/SP.J.1146.2012.01470.

YAN Junkun, JIU Bo, LIU Hongwei,Joint cluster and power allocation algorithm for multiple targets tracking in multistatic radar systems[J].&, 2013, 35(8): 1875-1881.doi: 10.3724 /SP.J.1146.2012.01470.

[6] GODRICH H, PETROPULU A, and POOR H V. Cluster allocation schemes for target tracking in multiple radar architectures[C]. Proceedings of Signals, Systems and Computers, Princeton, 2011: 863-867.doi: 10.1109/ACSSC. 2011.6190131.

[7] GODRICH H, PETROPULU A, and POOR H V. Sensor selection in distributed multiple-radar architectures for localization: A knapsack problem formulation[J]., 2012, 60(1): 247-260.doi: 10.1109/TSP.2011.2170170.

[8] GODRICH H, PETROPULU A, and POOR H V. Resource allocation schemes for target localization in distributed multiple radar architectures[C]. Proceedings of Signal Processing, Aalborg, Denmark, 2010: 23-27.

[9] GODRICH H, PETROPULU A, and POOR H V. Power allocation strategies for target localization in distributed multiple-radar architecture[J]., 2011, 59(7): 3226-3240.doi: 10.1109/TSP.2011. 2144976.

[10] GODRICH H, HAIMOVICH A, and BLUM R. Target localization accuracy gain in MIMO radar based system[J].2010, 56(6): 2783-2803. doi: 10.1109/TIT.2010.2046246.

[11] GARCIA N, HAIMOVICH A, COULON M,. Resource allocation in MIMO radar with multiple targets for non-coherent localization[J]., 2014, 62(10): 2656-2666. doi: 10.1109/TSP. 2014.

2315169.

[12] PANOUI A, LAMBOTHARAN S, and CHAMBERS J A.Game theoretic power allocation technique for a MIMO radar network[C]. International Symposium on Communications, Control and Signal Processing, Athens, 2014:2509-2512.

[13] PIEZZO M, AUBRY A, BUZZI S,. Non-cooperative code design in radar networks: A game-theoretic approach[J]., 2013, 63. doi: 10.1186/1687-6180-2013-63.

[14] RADMARD M, CHITGARHA M M, MAJD M N,Antenna placement and power allocation optimization in MIMO detection[J]., 2014, 50(2): 1468-1478. doi: 10.1109/ TAES.2014.120776.

[15] MA B, CHEN H, SUN B,. A joint scheme of antenna selection and power allocation for localization in MIMO radar sensor networks[J]., 2014, 18(12): 2225-2228.doi: 10.1109/LCOMM.2014.2365206.

[16] HE Q, BLUM R, GODRICH H,. Target velocity estimation and antenna placement for MIMO radar with widely separated antennas[J]., 2010, 4(1): 79-100.doi: 10.1109/ JSTSP.2009.2038974.

[17] BECK A, BEN-TAL A, and TETRUASHVILI L. A sequential parametric convex approximation method with applications to nonconvex trusstopology design problems[J].2010, 47(1): 29-51.

Resource Allocation Approach in Distributed MIMO Radar with Multiple Targets for Velocity Estimation

HU Hanying SUN Yang ZHENG Nae

(,,450001,)

In order to improve the velocity estimation accuracy for multiple targets in distributed MIMO radar, this paper analyses the influence of transmitted power and signal effective time width on the estimation accuracy, and a joint resource allocation algorithm is proposed. Firstly, a criterion minimizing the maximum Cramer Rao Lower Bound (CRLB) on the mean square error in multiple targets velocity estimation is derived, and the corresponding optimization model with transmitted power and signal effective time width is solved by SPCA (Sequential Parametric Convex Approximation) algorithm. Finally, simulations demonstrate that the velocity estimation accuracy is improved by the proposed algorithm. The results also reveal that signal effective time width has a greater impact on the velocity estimation accuracy than transmitted power.

Distributed MIMO radar; Multiple targets velocity estimation; Power allocation; Signal effective time width allocation

TN958

A

1009-5896(2016)10-2453-08

10.11999/JEIT151452

2015-12-22；改回日期：2016-05-10；網絡出版：2016-07-14

孫揚 sunyang_kd@163.com

胡捍英： 男，1961年生，教授，博士生導師，主要研究方向為無線通信和空間信息技術.

孫 揚： 男，1992年生，碩士生，研究方向為MIMO雷達技術、資源分配.

鄭娜娥： 女，1984年生，講師，博士，主要研究方向為MIMO雷達技術、無線通信和空間信息技術.