基于粒子群算法的三維固體火箭發動機藥形快速優化方法

崔輝如，唐國金

?

基于粒子群算法的三維固體火箭發動機藥形快速優化方法

崔輝如，唐國金

（國防科技大學航天科學與工程學院，長沙，410073）

在高體積裝填分數前提下，如何提高發動機的結構完整性是固體火箭發動機藥形優化設計面臨的主要問題。通過提出基于粒子群優化算法（PSO）的三維固體火箭發動機藥形快速優化設計方法，采用MSC.Patran的二次開發工具PCL實現某三維固體火箭發動機藥柱的參數化建模，在不改變體積裝填分數的前提下，分別采用PSO算法和遺傳算法（GA）完成該發動機藥形的優化設計。結果表明，兩種方法均能滿足優化設計要求，但PSO算法比GA算法的計算時間縮短了42％，所提方法可快速實現固體火箭發動機藥形優化設計，提高復雜三維固體火箭發動機的結構完整性能。

藥形優化；粒子群優化算法；體積裝填分數；結構完整性

0 引 言

新一代大射程、高機動性固體導彈要求發動機具有高體積裝填分數。然而，體積裝填分數的提高將降低發動機的結構完整性能。因此，在滿足發動機體積裝填分數要求的同時，提高發動機的結構完整性尤為重要。

固體火箭發動機的藥形優化設計一直是研究人員十分關注的重要課題。蒙上陽等[1]研究了傘盤結構參數對藥柱應力應變場的影響，通過藥形參數優化，提高低溫載荷下藥柱的結構完整性能；夏冰戈等[2]利用ACIS圖形系統和Abaqus軟件建立了發動機的參數化模型，并利用遺傳算法（Genetic Algorithm，GA）在燃燒恒面性的前提下完成了某翼柱形藥柱的形狀優化；彭超等[3]利用神經網絡遺傳算法對推進劑應力釋放槽進行優化設計，降低了應力釋放槽頂部的最大Mises應變；李磊等[4]將GA算法與參數化建模方法相結合，以藥柱裝填分數最大為優化目標，藥柱的結構完整性能不降低為約束條件，實現傘盤結構藥柱的形狀優化設計；張維星等[5]利用MSC.Patran中的PCL語言建立某三維翼型藥柱的參數化模型，采用GA算法對其進行優化設計，得到滿足體積裝填分數前提下的最優藥形。綜上所述，GA算法已經被廣泛應用于發動機的藥形優化設計中，但是在GA算法中，信息只能在染色體間共享，種群向最優區域移動的速度比較均勻，優化效率比較低，延長了研發周期。特別是對于某些需要快速完成的優化任務，GA算法的局限性顯得尤為突出。

為了達到預定的技術指標，固體發動機多采用三維復雜藥形結構，建模分析時一般需要較大的網格規模滿足精度要求。同時，考慮推進劑材料的粘彈特性，完成一次發動機結構完整性計算往往耗時較長。所以，在進行發動機優化設計時，必須考慮算法的收斂性，這對于縮短設計周期，降低研發成本具有重要意義。

本文采用MSC.Patran中的PCL語言和MSC.Marc軟件實現了某三維固體火箭發動機幾何建模的參數化和結構完整性分析流程的自動化，并分別基于GA算法和收斂性能較好的粒子群算法（Particle Swarm Optimization，PSO）[6]，在滿足體積裝填分數的前提下，分別對該發動機進行了藥形優化設計。

1 發動機參數化建模

1.1 發動機有限元模型

對固體火箭發動機進行結構完整性能分析的基礎是建立有限元計算模型。以某星孔發動機為例，考慮到該發動機的三維幾何模型具有循環對稱性，而且所作用的溫度、內壓等外載荷也具有循環對稱性。因此，可以利用其循環對稱性建立該發動機的1/6模型，以減少單元數量。為便于建模，在不影響藥柱結構分析結果的前提下，忽略噴管、點火器等結構部件以及工藝上的一些細節，建立以殼體、絕熱層和藥柱為主要部件的發動機有限元模型，如圖1所示。

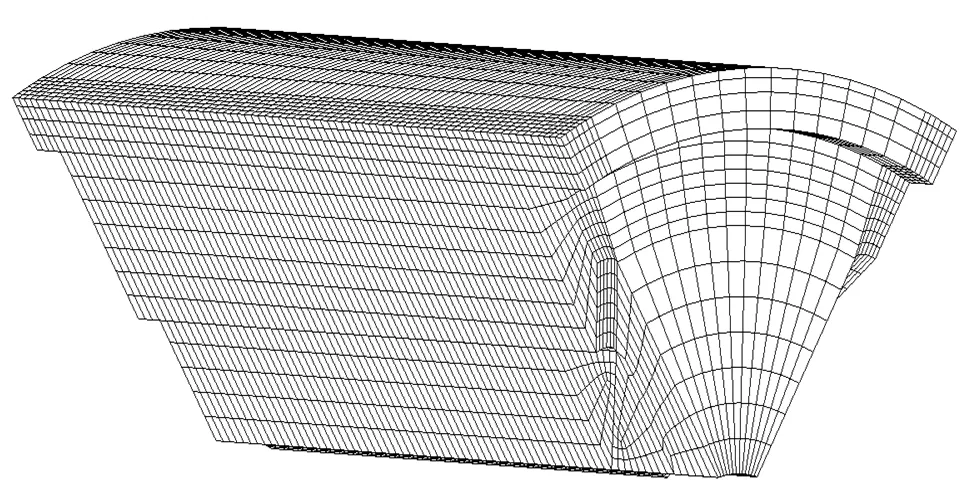
圖1 發動機有限元模型

圖1中的發動機尾部兩側設有翼槽。一般來說，翼槽段是該類發動機易發生應力集中的地方，所以在劃分翼槽段的網格時，通常會采取加密措施。圖2為如圖1所示發動機模型尾部有限元網格正面和反面的局部放大圖。

a）正面放大

b）反面放大

圖2 發動機尾部的放大示意

1.2 材料參數定義

假設發動機的殼體、絕熱層為彈性材料，藥柱為均勻、各向同性、泊松比為常數的線粘彈性熱流變簡單材料，計算時所需材料參數如表1所示。

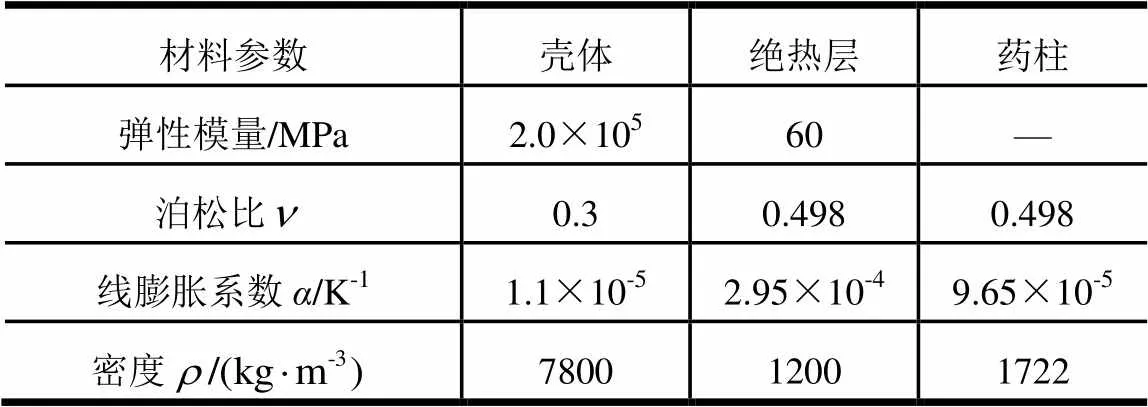
表1 發動機基本材料參數

MSC.Marc軟件利用廣義Maxwell模型描述粘彈性材料的本構關系，因此，需要定義剪切松弛模量和體積松弛模量的Prony級數。通過單向拉伸試驗，可得推進劑拉壓松弛模量的主曲線。經過非線性最小二乘法數據擬合，可以得到其Prony級數表達式，即：

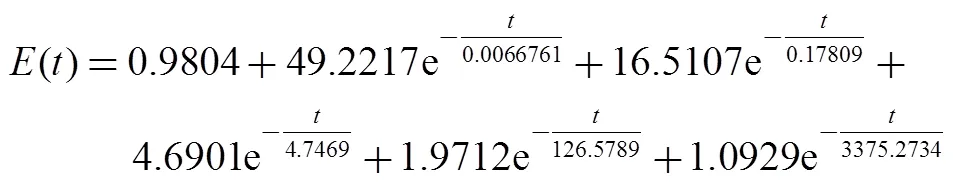
（2）

在參考溫度s=293.15 K時，利用最小二乘法可以得到WLF方程的系數：1=20.012 1和2=573.037 1。

1.3 載荷及邊界條件

固體發動機實際載荷歷程經歷3個階段：

a）第1階段：固化降溫階段。發動機在1天內從零應力溫度58 ℃線性降溫到常溫20 ℃。

b）第2階段：低溫試驗階段。發動機從常溫線性降溫到低溫-45 ℃，假設在第1和第2階段中的各個時刻整個發動機處于均勻溫度場中。

c）第3階段：低溫試車階段。發動機在0.3 s的時間內，內壓力達到峰值9.0 MPa。

在進行發動機有限元分析時，為避免出現剛體位移而導致剛度矩陣的奇異，將發動機殼體前端節點的6個自由度進行約束。同時，施加對稱邊界條件，對發動機1/6模型兩個側面上的環向位移進行約束。

1.4 參數化建模方法

MSC.Patran提供了二次開發工具PCL，利用PCL可以建立發動機的參數化模型，為發動機結構優化提供有效手段[7]。考慮發動機的其他約束條件，本文選取星孔肉厚、星尖橢圓長半軸長、翼槽傾角等作為參變量（詳見3.1節），利用文獻[7]中的方法建立該發動機的參數化模型。

2 粒子群算法

2.1 基本原理

PSO算法是Kennedy和Eberhart[8]受啟發于鳥群聚集覓食活動而提出的。PSO算法類似于GA算法，是一種基于迭代的優化算法，但是PSO算法卻沒有GA算法中復雜的交叉和變異操作，所以算法較簡單，運行效率較高。PSO算法將群體中的每個個體視為多維搜索空間中的一只鳥，也稱為粒子，這些粒子在搜索過程中不斷調整自己的位置和速度，而調整的依據是在搜索中所積累的經驗。粒子通過不斷地搜索，逐漸逼近最優解所在的區域，并最終找出全局最優解[9]。

2.2 算法的實現

在搜索空間中，每個粒子都有自己的參數，即位置和速度。粒子的位置用于表示優化問題的優化變量，粒子的速度決定其飛行方向和速率大小，每個粒子性能的優劣程度取決于優化目標所建立的適應度函數。第個粒子在迭代到第代時的位置和速度分別為

（4）

式中為優化變量的個數，同時每個粒子都有一個優化目標所決定的適應度函數。

PSO算法流程是求解空間中隨機初始化粒子的位置和速度。初始化的粒子第維（1≤m）的位置（1）和速度（1）為

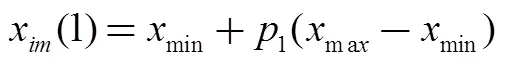
（6）

粒子群在迭代到第代時將產生2個極值：個體極值，即單個粒子在次迭代過程中得到的最優解，其位置表示為；全局極值，即所有粒子在次迭代過程中找到的最優解，其位置表示為。在得到上述2個極值后，第（+1）迭代時粒子的第維（1≤m）速度和位置可以根據下式得到，即：

（8）

式（7）中第1項為慣性項，目的是使粒子具有搜索全局空間的趨勢；第2項為認知項，表示粒子本身對改進方向的思考；第3項為社會項，表示粒子間的最優信息參與了共享。

粒子群經過多次迭代，直到找到足夠好的適應值或達到預設的最大迭代次數。PSO算法的流程如圖3所示。

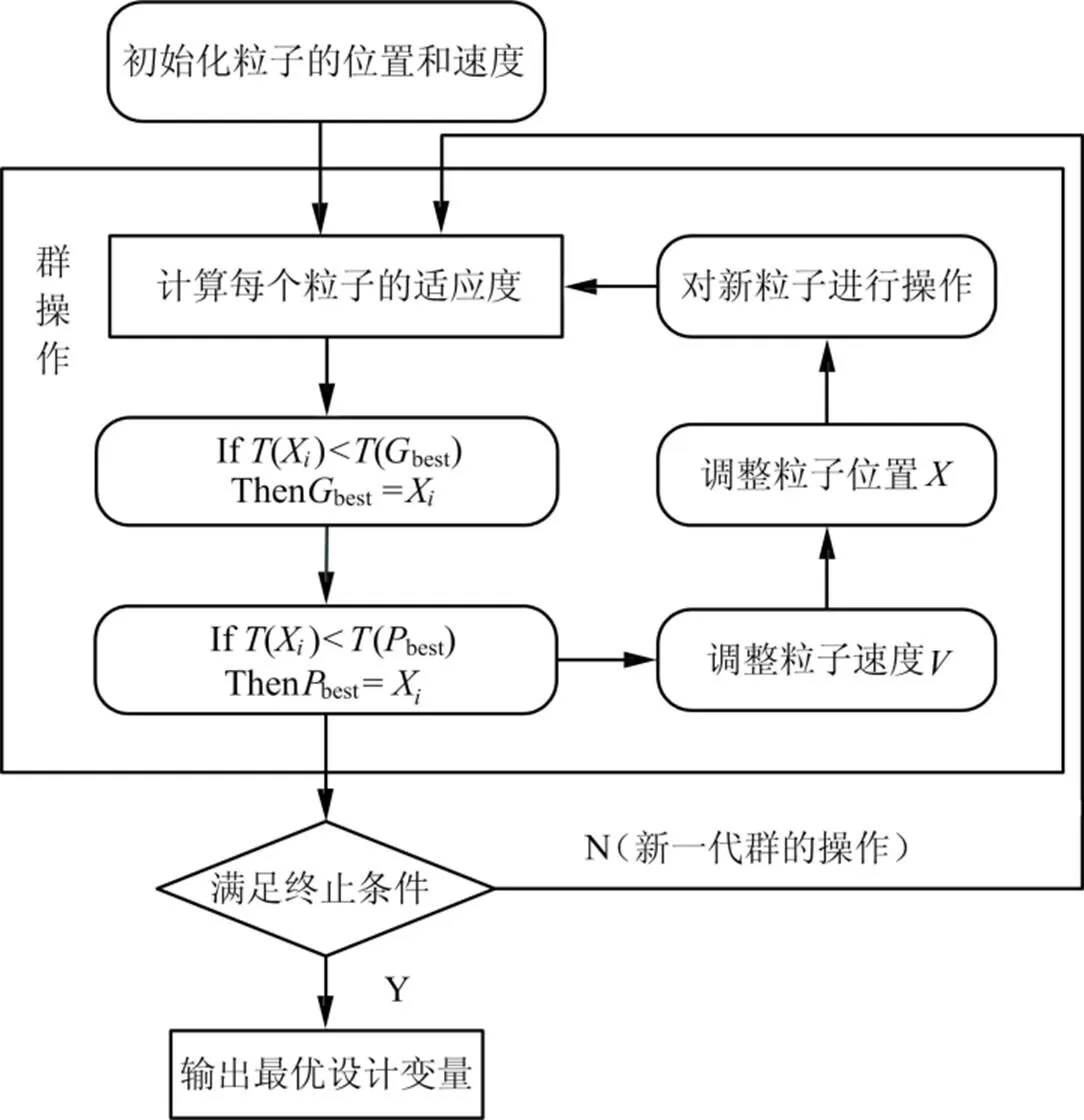
圖3 粒子群算法流程

3 優化實例

3.1 優化設計

初始階段，按照圖1中原始尺寸計算得到發動機藥柱應變云圖（見圖4），藥柱的最大等效應變為26.7%，發生在翼槽位置，體積裝填分數為71.42%。總體要求優化前后發動機的體積裝填分數不能小于70%。因此，問題轉化為在體積裝填分數不小于70%的前提下，使藥柱的最大等效應變最小。該優化問題的數學模型為

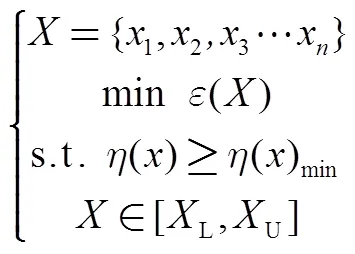
圖4 優化前藥柱等效應變云圖

為了避免發動機設計方案的較大調整，在優化過程中，不改變發動機藥柱的拓撲結構，僅通過改變藥柱應力集中位置的形狀和尺寸進行藥形優化。同時，必須控制所選幾何參數在較小范圍內變化，以確保發動機初始燃面變化不大，不影響發動機的內彈道性能。

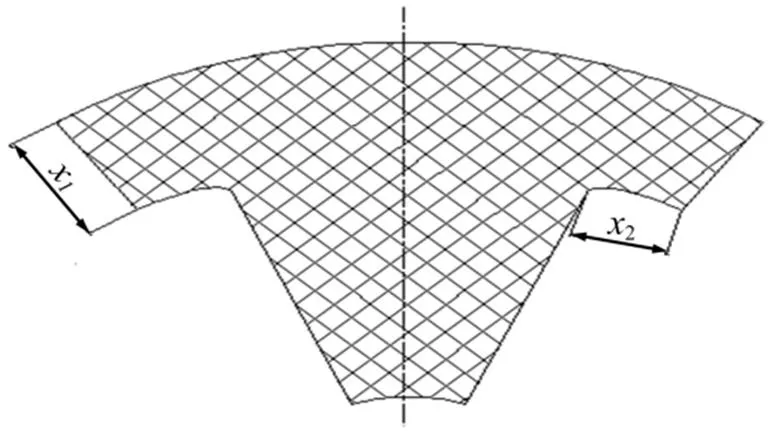
圖5 A點處藥柱橫截面示意

優化參數范圍選取的原則是：在優化前后發動機燃燒室的初始燃面面積變化在5%以內。為避免參數間的不協調而導致出現異常解，需要預先對參數的取值范圍進行檢驗。

傳統的優化設計方法對目標函數和約束函數的連續性與可微性有較高要求，不宜采用。近些年逐步發展起來的啟發式算法給類似問題的解決帶來了希望，其中PSO算法、GA算法等應用較為廣泛。GA算法需要進行交叉、變異等操作，過程復雜；而PSO算法調用參數少，操作簡單，并能快速收斂于最優解。在PSO算法中，需要定義個體的適應度函數，以表征個體對環境的適應能力。適應值的大小不僅與目標函數相關，還與約束條件相關。粒子的適應度函數是由優化目標函數和約束函數構成的罰項組成的罰函數,對上述優化問題，適應度函數定義為

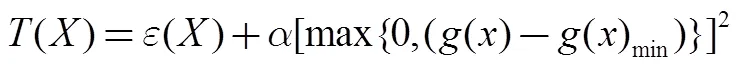
3.2 優化結果

為比較2種算法的優缺點，分別采用PSO算法和GA算法對本文問題進行優化。2種算法均設置相同的種群數和適應度函數。

表2為2種算法優化結果的對比。

表2 優化結果

由表2可以看出，PSO算法和GA算法得出的形狀最優藥柱的最大等效應變分別為20.90%和21.30%，與初值相比，藥柱最大等效應變分別降低了21.7%和20.2%。優化前后體積裝填分數都降低了1.96%，但滿足最小裝填分數的要求。由以上分析可以得出PSO算法優化效果更加顯著。

采用PSO算法和GA算法優化后得到的藥柱等效應變云圖如圖6所示，優化歷程如圖7所示。

a）PSO算法

b）GA算法

圖6 優化后藥柱等效應變云圖

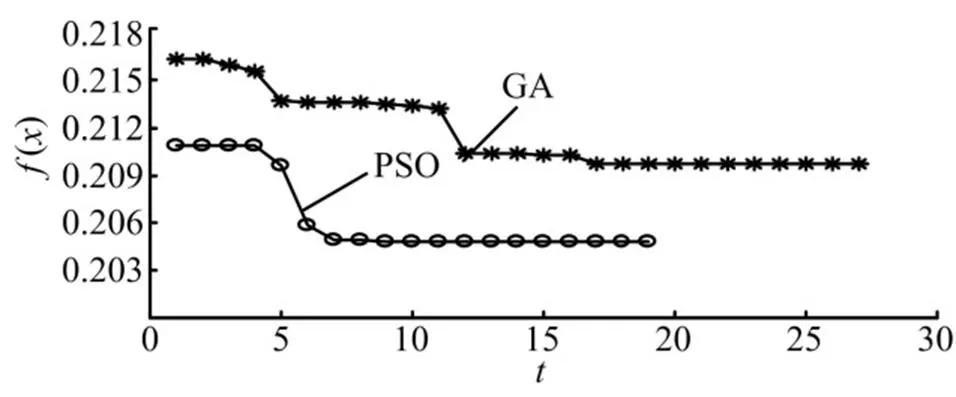
圖7 藥柱算法優化歷程

—算法迭代次數；()—種群在第代適應度函數的最小值

從圖7可以看出，2種算法都能得到最優解，但是實際分析計算過程中，與PSO算法相比，GA算法要多進行8代才能收斂到最優值。對于種群數目為20的情況，每進行一代，要進行20次分析計算。每進行一次發動機結構完整性的計算需1 h，完成整個優化過程PSO算法比GA算法快了6.6天，即PSO算法比GA算法減少近42%的計算時間。

4 結 論

基于MSC.Patran的二次開發語言PCL對某實際三維發動機進行了參數化建模，提出利用收斂性較好的PSO算法對發動機藥形進行優化的方法。在優化結果方面，PSO算法優化出的藥形對應的最大等效應變比原始藥形最大等效應變降低了21.7%，比GA算法優化效果顯著；在優化效率方面，PSO算法比GA算法具有更好的收斂性，優化時間減少了42%，優化代數減少了8代，優化效率明顯提高。PSO算法比GA算法在復雜三維固體火箭發動機藥性優化方面具有顯著的優勢。因此，本文提出的方法可用于復雜三維發動機藥形的快速優化設計。

[1] 蒙上陽, 唐國金, 雷勇軍. 低溫環境下固體發動機藥柱傘盤結構設計[J]. 推進技術, 2004, 25(5): 397-400.

[2] 夏冰戈, 鮑福延, 惠衛華, 劉旸, 劉強. 考慮燃燒恒面性和結構完整性的翼柱形藥柱形狀優化[J]. 固體火箭技術, 2013, 36(5): 620-625.

[3] 彭超, 陳軍, 封鋒, 岳小亮. 基于神經網絡遺傳算法的推進劑藥柱應力釋放槽優化設計[J]. 固體火箭技術, 2014, 37(2): 198-203.

[4] 李磊, 段靜波, 申志彬, 唐國金. 基于參數化建模的藥柱傘盤結構形狀優化[J]. 固體火箭技術, 2011, 34(5): 584-589.

[5] 張維星, 唐國金. 基于三維參數化建模的翼柱形發動機藥形優化[J]. 固體火箭技術, 2014, 37(4): 490-495.

[6] Kennedy J, Eberhart R C. Particle swarm optimization[J]. Proc. IEEE Int. Conf on Neural Networks, 1995(4): 1942-1948.

[7] 申志彬, 唐國金, 雷勇軍, 李磊. 基于Patran二次開發的星形藥柱結構分析與設計[J]. 固體火箭技術, 2009, 32(2): 175-179.

[8] 王允良, 李為吉. 粒子群優化算法及其在結構優化設計中的應用[J]. 機械科學與技術, 2005, 24(2): 248-252.

Fast Optimization Method of 3D Solid Rocket Motor Grain Based on Particle Swarm Algorithm

Cui Hui-ru, Tang Guo-jin

(College of Aerospace Science and Engineering, National University of Defense Technology, Changsha, 410073)

How to improve the structural integrity of solid rocket motor (SRM) with high loading fraction was one of the main problems during its configuration optimization design. Based on the particle swarm optimization(PSO), a fast optimization method is proposed to obtain the best 3D SRM grain configuration. Parameterized model of a 3D SRM grain was created with patran command language (PCL), the optimal project of grain configuration was done by using the PSO and Genetic Algorithm(GA) respectively without changing its volumetric loading fraction. The results showed that both of optimization methods met the requirements of optimization design, but the computation time of PSO was reduced by 42％ compared with GA. The method proposed could realize optimization design of SRM grain configuration efficiently，and the structural integrity of actual complex 3D SRM could be improved.

Grain shape optimization; Particle swarm optimization; Loading fraction; Structural integrity

1004-7182(2016)03-0019-05

10.7654/j.issn.1004-7182.20160305

V435+.21

A

2015-07-17

國家自然科學基金（11272348），國防科技大學科研計劃資助項目（JC13-01-03）

崔輝如（1991-），男，碩士研究生，主要研究方向為固體導彈結構完整性